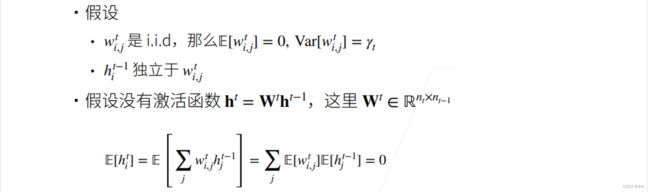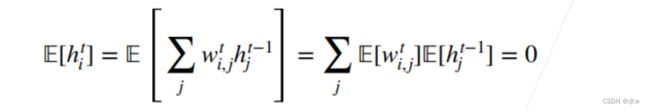【动手学深度学习PyTorch版】8 数值稳定性、模型初始化、激活函数
上一篇移步【动手学深度学习PyTorch版】7 丢弃法_水w的博客-CSDN博客
目录
一、数值稳定性
1.1 数值稳定性
◼ 数值稳定性常见的两个问题：
◼ 梯度爆炸：举例MLP
◼ 梯度消失
◼ 总结
1.2 如何使得训练更稳定
◼ 常见的方法
◼ Xavier初始：常用权重初始化的方法
一、数值稳定性
1.1 数值稳定性
◼ 数值稳定性常见的两个问题：
当神经网络变得很深的时候，数值非常容易变得不稳定。
假设，我们有个d层的神经网络，由于神经网络是个嵌套函数（一层一套），求导时链式法则变连乘（累乘）。那么使用链式法则来计算梯度：
这里我们可以看到，我们一共做了d-t次的矩阵乘法。
数值稳定性常见的两个问题：
- 梯度消失
- 梯度爆炸
◼ 梯度爆炸：举例MLP
① MLP：多层感知机。
② 对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵，常写为diag(a1, a2, ..., an)。
③ diag * W 把diag和W分开看。这就是个链式求导，diag是n维度的relu向量对n维度relu的输入的求导，向量对自身求导就是对角矩阵。
那么，关于t层的导数就是如上图中的形状。
假设我们使用relu函数作为激活函数，它的导数就是说如果x>0就为1 ，否则为0。所以就是一些1和0的对角矩阵，那么一些1和0的对角矩阵与Wi一乘，乘的时候，要么就是某一列留住了，要么就是全部变为0。
那么，就意味着，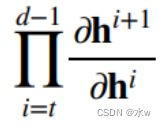
最后的值的一些元素就来自于其中没有被变成0的那一些列的乘法。
这里的问题就是说，如果d-t很大，值将会很大。-------这就是梯度爆炸。
那么，梯度爆炸的问题就是：超出值域变 infinity
如果我们的学习率调的稍微大一点点， 就会带来大的参数值，因为我们每一步都走的比较远，对权重的更新就会变得比较大。权重一大，就会带来梯度就会更大。那么，更大的梯度会带来更大的参数值，一直迭代，真个梯度就炸掉了。
如果我们的学习率调的非常小，每次对w的增加比较小，那训练就没有进展。
所以学习率比较难调，我们肯需要在训练过程中不断调整学习率。
◼ 梯度消失
对于激活函数，当激活函数的输入稍微大一点时，它的导数
就可能会变的很小，就变为接近0。就意味着可能会有d-t个小数的乘积，连续n个接近0的数相乘，最后的梯度就接近0，那么最终的梯度就会很小。--------梯度就消失了。
那么，梯度消失的问题就是：梯度值变成0，对16位浮点数尤为严重
- 训练无进展（不管如何选择学习率）；
- 对底层尤为严重：仅仅网络顶部（数据入口）训练好，底部训练不好。这就意味着不管让神经网络多深，底部的那些层跑不动，这就与一个很浅的神经网络是没有本质区别的。
◼ 总结
1.2 如何使得训练更稳定
◼ 常见的方法
我们的一个核心问题是：如何使得训练更稳定？就是说让梯度不要太大，也不太小。
目标：梯度值在合理的范围之内。那么几个常见的核心思想的方法：
- 乘法变加法：ResNet、LSTM；
- 归一化：例如变为标准正态分布；
- 梯度剪裁；
- 合理的权重初始化和激活函数；
合理的权重初始值和激活函数的选取可以提升数值稳定性。
那么我们如何合理的权重初始化和激活函数？
◼ Xavier初始：常用权重初始化的方法
我们可以让每层的输出和梯度都看做随机变量，如果我让它们的均值和方差都保持一致，这样会比较好。
假设对所有正向的i和t都是均值为0，方差为a；对所有反向的i和t都是均值为0，方差为b，
那么如何做合理的权重初始化？
在训练开始的时候更容易有数组不稳定，因为随机初始化的话，有可能在最优解的附近，也有可能在很有的地方，很有可能不会很好。而原理最优解的地方的损失函数表面可能会很复杂，会很抖，一抖就会导致算出来的梯度就会特别的大，导致w就会变得大。
一般来说，在最优解的附近会比较平一些，梯度就比较小。我们之前一直使用均值为0，方差为0.01的正态分布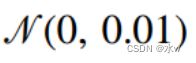
来随机初始我们的权重， 这有可能对一个小网络是没有问题的，但是对于一个大的深度神经网络切实不能保证。
那么，要满足我们之前的所有假设，输出和梯度的均值和方差都在一个常数的话，我们应该怎么办？
回到MLP的例子，我们做一些假设：
假设权重是一些独立同分布，那么每一个元素的均值就是0，方差就是
。那么，这当前层的的输入hi^t-1，就也是独立于我当前层的权重。假设没有激活函数，那
，
做了这些假设之后，两个独立同分布可以写开，我们的计算就变成了下面这样：
对于正向方差，
对于反向均值和方差， 跟正向情况类似，
均值都是为0的，那么想要让两个方差一样，就需要满足两个条件，
但是这两个条件很难同时满足，因为其中的第t层输入的维度nt-1和第t层输出的维度nt是我们不能控制的，除非第t层输入维度刚好等于输出维度。
那么，怎么做呢？不能满足同时， 那我们可以做一点权衡，取折中。-------Xavier初始
意味着给定我这个神经网络的当前层的输入和输出层的大小，那么我就能确定当前权重的大小。
我们之前假设是没有激活函数，那么为了简单起见，现在我们假设线性的激活函数，使得均值/期望=0，那我这个激活函数一定是过原点的。
计算方差时，我要想使得方差不变，那么就只能使得
。
对于反向均值和方差， 跟正向情况类似，
那么意味着，这个激活函数必须是f(x)=x，检查一下我们的激活函数。
发现对于tanh和relu来讲，在零点附近确实是近似到一个f(x)=x，问题不大，也就是说在零点附近满足我们之前的假设要求。
但是对于sigmoid来讲，有问题，不过原点，不满足我们之前的假设要求，需要调整。调整之后的sigmoid可以从图中看到也是经过原点的，基本上f(x)=x。