2023牛客寒假算法基础集训营1
题解 | #2023牛客寒假算法基础集训营1#_牛客博客 (nowcoder.net)
//本人能力有限,以下只附上本人get到的题,其他参考以上链接或其他
A World Final? World Cup! (I)
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
众所周知,2022年是四年一度的世界杯年,那么当然要整点足球题。本题需要你模拟一次点球大战。
假设对战双方为A和B,则点球大战中双方会按照ABABABABAB方式来罚点球,即两队交替罚点球、各罚五次、A队先罚。点球有罚进和罚不进两种结果,罚中的一方加一分。
其判断胜负的规则为得分多者获胜,而若在罚完某一球后(无论是哪队罚的),当前双方比分已经使得无论之后的罚球结果如何都不会影响比赛的结果,则此时比赛结束。特别地,若直到10球踢完都没有分出胜负则再继续加踢更多的点球。
现在,给出接下来双方10个点球的结果,你需要判断点球大战会在踢完几球时结束,或指出10球内没有分出胜负。
输入描述:
输入第一行包含一个整数T(1≤T≤1024),表示样例组数。 每组测试用例包括一个长度为10的字符串S,第i个字符表示第i个点球的结果,0表示罚不进、1表示罚进,保证不会出现其他字符。
输出描述:
对每组测试用例,输出一个整数,表示点球大战会在第几回合结束,若10轮之内没有分出胜负,输出−1。
示例1
输入
3 1111111111 1111111110 0101011010
输出
-1 10 6
说明
对于第二组样例,踢完前9球时双方比分5:4,此时最后一球若不进则比分是5:4且A赢、若进则比分是5:5进入加踢,因此9球时不能判断最终结果,踢完10球才确定B输。
对于第三组样例,踢完六球时比分为0:3,此时可以确定B一定会赢。
//下面是本人错误代码
//先阐述本人理解,关键点在于题目中我描红的部分, 要想提前结束比赛,只能在第6个球及其以后的球结束后才能实现,也就是答案除特殊情况外,只能是6-10。
我们以第6个球结束为例,只有产生0:3或者3:0的结果才能结束比赛,因为后面即使对方全进,自己一个不进,那么比分3:2或2:3,还是赢,也就是结局已定,继续比赛没有意义,所以我们提前结束。
然后本人的考虑点就从输出结果去判定,要想输出这个结果需要满足什么条件。
#include
using namespace std;
int main(){
int n,i,a,b;string s;
cin>>n;
getchar();
while(n--){
a=0;b=0;
cin>>s;
for(i=0;i //下面这个博主的代码易理解
题解 | #A World Final? World Cup! (I)#2023牛客寒假算法基础集训营1_牛客博客 (nowcoder.net)
这是参考该博主后的正确代码,主要是跳出循环那两个判断,首先,k用来记位置,k为0说明两个打平,然后输出-1,然后a,b分别记录A和B得分,当每一个回合结束,a,b差的绝对值为>=3的时候即可结束,这点非常容易理解,最后这个判断非常好,a1,b1分别记录此时A和B是第几个,正如原博主所述:计算如果一方赢下接下来的所有比赛能不能赶上甚至超过对方,如果可以,继续执行循环;不行的话直接结束比赛。我们以10101111xx为例,无论最后两个x是什么,比赛可以在第8这个位置结束了,因为现在是4:2,而后面可能是4:3,4:2,5:3,5:2,比赛结果毫无悬念,此时a=4,b=2,b1=4,4>2+5-4,所以记录位置,然后退出。或者我们这样思考,写成a-b>5-b1,5-b1可以理解为全进状态下,b最多还能进几个球,如果这个结果大于或等于前面a-b,那么就产生输赢的不确定性。
其实没那么复杂,大家举几个例子推一下,然后就能get了。
#include
using namespace std;
int main(){
int t,i,a,b,a1,b1,k;
cin>>t;
string s;
while(t--){
cin>>s;
a=0,b=0,a1=0,b1=0,k=0;
for(i=0;i<=9;i++){
if(i%2==0){
if(s[i]=='1')a++;
a1++;
}
else{
if(s[i]=='1')b++;
b1++;
}
if(abs(a-b)>=3&&i%2==1){k=i+1;break;}
if(a>b+5-b1||b>a+5-a1){k=i+1;break;}
}
if(k==0)cout<<"-1\n";
else
cout< C 现在是,学术时间 (I)
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
北京IT大学(BIT)计算机学院为了在下一轮学科评估中让计算机学科获得A+的评定结果,进行了如引进强大的老师、加强课程之类、提高授课质量等多方面的努力。而为了提高学科评估中,学术成果一项的得分,计算机学院的院长打算通过重新分配论文的方式使得学院里所有教授的H指数值之和尽可能大。
具体来说,H指数用于粗略的评估一位教授的学术水平。一位教授可以发表多篇论文,每篇论文有一个引用量。定义一位教授的H指数为使得"该教授发表的所有论文中,有至少H篇论文的引用量大于等于H"这一命题成立的最大的H。
现在,院长发现学院里的每位老师当前的发表文章数都为0,且恰好每人都有一篇写好的论文未发表,由于院长很懂学术界,他也可以准确的预知到每篇文章发表后的引用量。院长决定以最优的方式重新分配这些论文,他可以任意指定一篇论文由哪位教授发表。规定每篇论文只能被一位教授发表,一位教授可以发表多篇论文。
假设重新分配并发表后第i位教授的H指数为hi,院长希望最大化Σi=1nhi\Sigma,即所有教授的H指数之和最大。请你帮院长计算出这一最大的值为多少。
输入描述:
输入第一行为一个正整数T(1≤T≤105),表示样例组数。 每组样例包括两行。 第一行是一个正整数n(1≤n≤105),表示北京IT大学计算机学院的教授数量;第二行包括n个非负整数,第i个数字ai(0≤ai≤109)表示第i位教授写好但未发表的文章在发表后会获得的引用量。 保证每组数据所有用例的n之和Σn≤5×105\Sigma。
输出描述:
对于每组样例,输出一个整数,表示Σi=1nhi\Sigma最大的值为多少。
示例1
输入
2 3 6 5 4 2 10 0
输出
3 1
说明
对于样例一,一种可能的方案是把三篇论文(引用量分别为6,5,4)都让第一个教授发表,这样第一个教授有三篇引用量大于等于三而没有四篇引用量大于等于四,因此有h1=3,h2=0,h3=0,可以证明此时有Σi=1nhi\Sigma_{i=1}^n最大,其值为3。
注:题目复制过来会重复两遍且符号乱码,原题请看链接。
//这题做出来的时候我是比较惊讶的,感觉太简单,但其实就是这么个道理,除了引用量为0的不统计之外,其他的无论你怎么分,和平均每人发一份的结果是一样的,也就是自己发自己的就行,不需要别人代劳。
#include
using namespace std;
int main(){
int t,n,x,a;
cin>>t;
while(t--){
a=0;
cin>>n;
while(n--){
cin>>x;
if(x)a++;
}
cout<
H 本题主要考察了DFS
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
shino是一名喜欢拼图的女高中生,他最喜欢玩的拼图是黄金拼图(指把爱丽丝和九条可怜拼在一起),不过这和本题并没有什么关系。 点我看原番 点我看名场面
某天,shino发现了一款叫做《拼图啊》(PTA)的全新拼图游戏,shino希望你能编写程序帮她开发这个游戏的外挂。
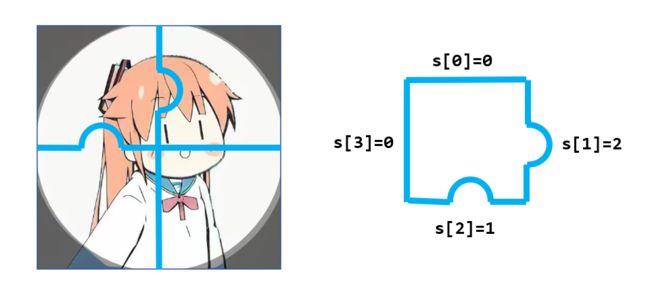
PTA的拼图由n∗n个大小为1∗1的拼图块组成,每个拼图块都是在正方形的1∗1拼图块基础上生成的,生成方法为:对于每一条边,可以选择不变、向里削出一个半圆形的缺口、向外补上一个半圆形的凸出三种操作之一。因此,一个拼图块可以由一个长度为4的字符串描述,四个字符分别表示上、右、下、左四条边进行的操作,上述三种操作依次记为0,1,2。
例如,下图的左图为一个2∗2的拼图。而右图为左图中左上角的一块1∗1拼图的字符串描述,由于其上、右、下、左进行的操作分别为不变、凸出、缺口、不变,因此这块拼图对应的字符串为0210。
每块拼图还有一个制作成本p,制作成本正比于面积,而拼图中削去的缺口和补上的凸出面积又相同,因此对于一块削去了x个半圆、补上了y个半圆的1∗1拼图,其制作成本p=10−x+y。如上图右图中拼图的成本为p=10−1+1=10。
现在,PTA会从所有拼图中随机隐藏一块,并打乱剩下的n2−1块拼图,告诉了你它们的形状对应的字符串表示(由于拼图上绘制了可供辨识的图案,因此给出的拼图形状都是各拼图块正面朝上、未经旋转的正确形状)。
PTA需要你完成这一拼图游戏,还原拼图原来的样子。你需要回答隐藏起来的那块拼图的制作成本来证明你成功完成了拼图。
输入描述:
输入第一行是一个整数T(1≤T≤100),表示测试用例组数。 对于每组测试用例: 第一行为一个正整数n(2≤n≤20),表示拼图的大小。 接下来n2−1行,每行一个长度为4的字符串,表示一块拼图正面朝上、未经旋转的形状。保证字符串中只含0,1,2三种字符。 输入数据保证n^2-1块拼图是从一个合法的n∗n拼图中按如题面所述的过程获得的。
输出描述:
对每组样例输出一个整数,表示你在拼出拼图后所计算出的缺失拼图块的制作成本。
示例1
输入
1 2 0001 0000 0210
输出
11
说明
样例即为题目中图片所给的例子,具体来说,输入的三个字符串分别对应图中右上角、右下角、左上角的拼图块。 通过编程将拼图还原,可以发现缺的是左下角的那一块,其形状为2000,因此制作成本为p=10−0+1=11。
//根本不需要用到dfs,(本人对dfs不太敏感,get不倒位), 题目描述中告诉我们,1是凹进去,用x计数,2是凸出来,用y计数,并用10-x+y表示每块的制作成本,而完整的成本每块就是10,那么总成本就是40,我们用x统计总的削去的,y统计总的补上的,那么就是30-x+y,那么剩下的就是10+x-y了。
#include
using namespace std;
int main(){
int t,n,i,x,y;
string s;
cin>>t;
while(t--){
x=0,y=0;
cin>>n;
n=n*n-1;
while(n--){
cin>>s;
for(i=0;i<4;i++){
if(s[i]=='1')x++;
if(s[i]=='2')y++;
}
}
cout<<10+x-y<
L 本题主要考察了运气
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
《P--j--- S-k--》是一款S-g-发行的C132−keyC_{13}^{2}-keyC132−key音乐游戏,游戏中除了主打的-家虚拟歌姬角色外,还有大量人设饱满的原创角色。而知名算法竞赛选手J----ly就是该游戏的玩家。现在,你想猜出J----ly在该游戏中最喜欢的原创角色是谁。
一些可以参考的资料(对做题并没有用):点我 点我 点我 点我
该游戏中共有202020名原创角色,分别属于555个团体,每个团体恰好444个人。为了猜出J----ly最喜欢的角色,你可以向他提以下两类问题(J----ly会如实回答):
1、ta属于第i(1≤i≤5)i(1\leq i\leq 5)i(1≤i≤5)个团体吗?
2、ta是第i(1≤i≤5)i(1\leq i\leq 5)i(1≤i≤5)个团体的第j(1≤j≤4)j(1\leq j\leq 4)j(1≤j≤4)个人吗?
你需要不断向J----ly提问,直到自己100%确定的知道J----ly最喜欢的角色是谁才停止提问。
现在,你想知道,在选择最优的提问策略使提问数尽可能少的情况下,你的期望提问次数是多少次?本题要求输出该期望次数。
特别地,好心的出题人为了让这题有100%的通过率,把这题出成了选择题的形式,选项含义见输出描述部分。
下面给出一种可能的提问示例:
问题一:ta属于第333个团体吗?回答:不属于。
问题二:ta属于第111个团体吗?回答:不属于。
问题三:ta是第222个团体第222个人吗?回答:不是。
问题四:ta是第444个团体第333个人吗?回答:是。
此时,你通过四个问题,能100%确定J----ly最喜欢的角色是第444个团体的第333个角色,提问次数为444。
输入描述:
本题没有输入,直接输出你的答案。
输出描述:
如题面所述,本题很好心,是个选择题,共有100个选项(最多99发罚时就可以保证通过此题辣),选项编号为111至100100100,第iii个选项为3.45+0.05∗i3.45+0.05*i3.45+0.05∗i,如第111个选项为3.503.503.50,第101010个选项为3.953.953.95。
你需要选择出与答案最接近的选项的编号(一个1至100的正整数)。
示例1
输入
本题无输入
输出
50
正如题目所言,就是看运气,和题目描述没有丝毫关系,并且还看不太懂,和输出结果也没关系,而是输出描述的最后一句,我也是看到别人提交了70多次才反应过来,就是最笨的办法从1到100挨个评测,你 要是运气好直接输32一次通关,运气不好,那就99次。
#include
using namespace std;
int main(){
cout<<"32";
return 0;
} D 现在是,学术时间 (II)
据说是简单题,不过我题目都没看;
K 本题主要考察了dp
题解 | #K 本题主要考察了dp #2023牛客寒假算法基础集训营1_牛客网 (nowcoder.com)
//比起真的用dp去解决的,这个代码简单不少,但有待理解。
M 本题主要考察了找规律
以为是找规律的时候,去看了下题目,没搞出来,解析用的是dp(动态规划)。