决策树算法之分类回归树 CART(Classification and Regression Trees)【2】
上一篇文章主要介绍了分类树,下面我们再一起来看一下回归树,我们知道,分类决策树的叶子节点即为分类的结果;同理,回归树的叶子节点便是连续的预测值。那么,同样是回归算法,线性回归和决策树回归有什么区别呢?区别在于,前者拟合的是一条直线,而后者却可以拟合非线性的数据,如下图中的数据就是用线性回归来拟合的:
当数据呈现非线性分布时,例如下面的数据,假设它统计了流行歌手的喜好程度和年龄的关系,该系数值在 10 岁之前很低,接着在 10 到 20 岁时达到最高,但随着年龄的增加,该兴趣度会逐渐下降,如图所示:
上面的数据如果用线性回归来拟合,是这样的:
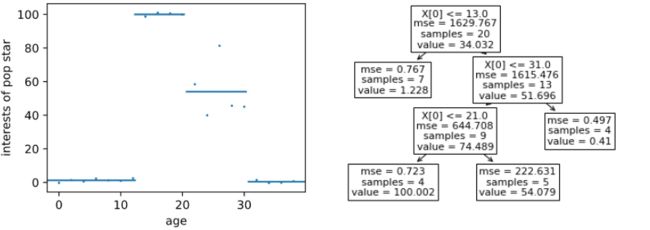
很明显,这样做会得到较大的 Bias,那么该数据就不应该使用线性回归这种简单的模型来表征,此时就需要用到非线性模型了,而回归树就是其中的一种。下边左图便是使用回归树对该数据进行拟合的结果,而右边是这棵树具体的样子:当 age 小于等于 13 时,结果为 1.228;age 大于 31 时,结果是 0.41;age 在 (13, 21] 的区域,结果为 100,剩下区域的结果为 54。
下面我们具体看一下这棵回归树是如何构建的
构建回归树
首先,我们在整个样本空间中选择一个阈值,该阈值可以将样本分为两部分,接下来分别对这两部分求出它们的均值,以均值作为预测值,计算所有数据的真实值到预测值之间的 SSR(Sum of Squared Residuals),SSR 本质上和 MSE(Mean Squared Error)的概念是一致的,都是衡量整体预测值和真实值之间的差异的,该差异越小越好。
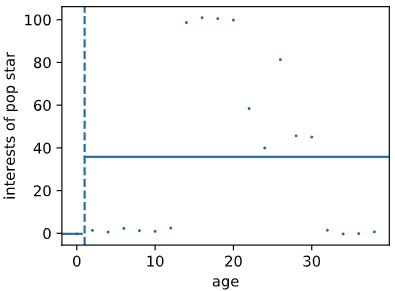
以本数据为例,刚开始我们选择的阈值 threshold 为 1,则下图中的样本被阈值(虚线)分为两部分,然后分别对左右两边的数据求平均,结果如图中两条水平实线所示,以水平线作为每个区域的预测值,接着我们对每个点,求它们离均值之间的差的平方(误差的平方),并把它们加起来,得到的结果就是 SSR。
上图中的 SSR 为
S S R = ( 0 − 0 ) 2 + ( 0 − 35.8 ) 2 + . . . + ( 0 − 35.8 ) 2 = 31358 SSR = (0-0)^2 + (0-35.8)^2 + ... + (0-35.8)^2 = 31358 SSR=(0−0)2+(0−35.8)2+...+(0−35.8)2=31358
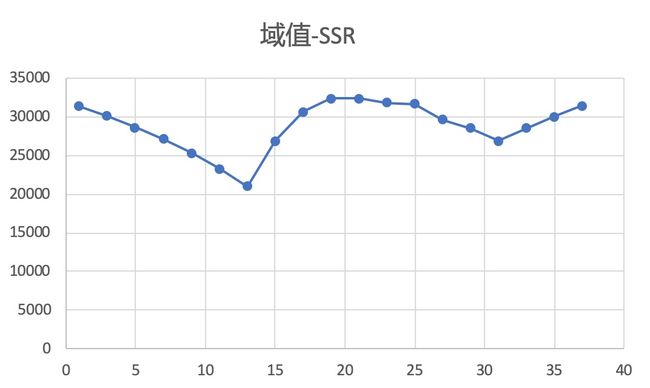
每算完一个 SSR,都要改变阈值,用同样的方法在新的分类下算一个新的 SSR,如此循环下去,直到遍历完所有可能的域值,此时我们就可以作出一个「域值-SSR」的关系图,如下:
以上过程的目的是为了找一个阈值,可以使得 SSR 达到最小,而可以使 SSR 最小的域值就是我们的树根。反过来理解一下,即我们需要在特征空间(定义域)找到一个值,该值把样本分为两类,分别对应了 2 个不同的预测结果,此预测结果和样本真实值(值域)之间的差异要越小越好,在本例中,该值为 13,示意图如下:
和分类树一样,只要确定了树根的构建算法,后面构造其他节点实际上和构造树根是一模一样的,以上图为例,即分别以树的左右两边的子样本空间为整个样本空间,继续构造子样本空间的“树根”,实际上这就是递归,同时在递归的过程中,随着树的节点不断分裂,我们得到的残差(SSR)会越来越小。
需要注意的是,决策树如果不设限制,它的节点可以无限分裂下去,直到叶子节点中只包含 1 个元素为止,此时整棵树的残差达到最小值 0,这样做会让我们的模型在训练时得到很低的 Bias,但可想而知的是它的泛化能力很弱,即 Variance 很高,于是便过拟合了,这也是决策树容易过拟合的原因。
为了防止过拟合,通常有 2 个参数可以设置,一个是树的高度,另一个是叶子节点中最小样本的个数,本文中的模型对这两个参数的设置分别是 3 和 4;在真实环境中,叶子节点的样本数一般会设在 20 以上。
多维度特征的回归树
上面例子是使用单特征(年龄)来构建回归树,真实项目往往会有多个特征,此时我们该如何做呢?我们在原来的数据集中增加两个特征:性别和月支出,如下
| 年龄 | 性别 | 月支出 | 流行歌手喜好度 |
|---|---|---|---|
| 3 | male | 300 | 0 |
| 7 | female | 300 | 5 |
| 13 | female | 500 | 90 |
| 17 | male | 500 | 85 |
| 18 | female | 500 | 99 |
| 25 | male | 4000 | 75 |
| 30 | female | 5000 | 40 |
| 35 | male | 7000 | 0 |
现在我们知道了,构造决策树的要点在于树根的构造,多个特征的话,我们需要分别对每个特征,找出可以使 SSR 最低的阈值,根据前面学到的知识,对年龄来说,可使 SSR 最低的域值是 「age<=7」,此时 S S R a g e = 7137 SSR_{age}=7137 SSRage=7137;
同理,对月支出来说,可使 SSR 最低的域值是 「expense<=300」,此时 S S R e x p e n s e = 7143 SSR_{expense}=7143 SSRexpense=7143。
而性别这个特征比较特别,它只有一个阈值,其 S S R g e n d e r = 12287 SSR_{gender}=12287 SSRgender=12287。
以上三个数字,有兴趣的同学可以根据上面的表格自己算一下,最终我们选择 SSR 最低的特征及其阈值作为根节点,即「age<=7」。
知道根节点如何产生后,后面节点的生成就好办了,于是多维特征的回归树我们也构建出来了。
总结
本文主要介绍回归决策树的生成算法,及回归树中比较重要的参数为:树的深度和叶子节点中最小的样本数,这两个参数可以防止过拟合问题。
最后我们一起学习了从多个特征维度来产生回归树,它和单维度特征的区别在于,每产生一个节点前,都需要计算每个特征的 S S R m i n SSR_{min} SSRmin 及其对应的阈值,最后取其中最小的 S S R m i n SSR_{min} SSRmin 对应的特征和阈值作为该节点。
参考资料:Regression Trees, Clearly Explained
相关文章:
- 决策树算法之分类回归树 CART(Classification and Regression Trees)【1】