python实现GA求解基于多层编码的柔性作业车间调度问题

参考《matlab智能优化算法30个案例分析》

导入库

import numpy as np
import copy
import matplotlib.pyplot as plt
import matplotlib

数据（可选机器+加工时间）

machine_mat = np.array([[(3,10),(2,),(3,9),(4,),(5,),(2,)],
                        [(1,),(3,),(4,7),(1,9),(2,7),(4,7)],
                        [(2,),(5,8),(6,8),(3,7),(3,10),(6,9)],
                        [(4,7),(6,7),(1,),(2,8),(6,9),(1,)],
                        [(6,8),(1,),(2,10),(5,),(1,),(5,8)],
                        [(5,),(4,10),(5,),(6,),(4,8),(3,)]],dtype=object)

process_mat = np.array([[(3,5),(6,),(1,4),(7,),(6,),(2,)],
                        [(10,),(8,),(5,7),(4,3),(10,12),(4,7)],
                        [(9,),(1,4),(5,6),(4,6),(7,9),(6,9)],
                        [(5,4),(5,6),(5,),(3,5),(8,8),(1,)],
                        [(3,3),(3,),(9,11),(1,),(5,),(5,8)],
                        [(10,),(3,3),(1,),(3,),(4,7),(3,)]],dtype=object)

相关参数

job_nb = 6 # 作业数
op_nb = 6 # 操作数
machine_nb = 10 # 机器数
maxgen = 200 # 最大迭代次数
pop_size = 50 # 种群规模
cross_rate = 0.8 # 交叉概率
mutate_rate = 0.6 # 变异概率
total_op_nb = job_nb * op_nb # 工序总数

GA

编码

此处编码中机器部分是可选机器集的索引编码。如工件3的工序1可选机器（3，9），机器编码为1，代表工件3的工序1在机器9上加工。工件和工序均从0开始计数

# 编码示例
[4. 2. 4. 5. 5. 2. 4. 2. 1. 0. 1. 2. 5. 5. 1. 1. 4. 5. 1. 0. 0. 3. 5. 2.
 0. 4. 2. 0. 3. 4. 3. 3. 1. 0. 3. 3. 0. 1. 0. 0. 1. 0. 1. 1. 0. 1. 0. 0.
 0. 0. 1. 0. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 0. 0. 0. 0. 0. 0.]

解码

将染色体还原成三位数表示的工件加工顺序，如302表示工件3的第2道工序，工件和工序均从1开始计数

# 解码示例
[501. 301. 502. 601. 602. 302. 503. 303. 201. 101. 202. 304. 603. 604.
 203. 204. 504. 605. 205. 102. 103. 401. 606. 305. 104. 505. 306. 105.
 402. 506. 403. 404. 206. 106. 405. 406.]

适应度

[[ 0.  0.  6. 16. 18.  4. 16.  9. 18. 25. 24. 15. 25. 31. 32. 36. 25. 36.
  41. 44. 54.  9. 44. 63. 63. 54. 72. 68. 33. 59. 47. 72. 68. 73. 83. 84.]
 [ 6.  4. 16. 18. 25.  9. 25. 15. 24. 30. 32. 20. 31. 32. 36. 41. 33. 44.
  44. 54. 63. 16. 47. 72. 68. 59. 73. 71. 36. 66. 51. 75. 71. 83. 84. 87.]]

选择

交叉

使用order crossover(OX)交叉算子
示例如下：
（1）父代母代

[5. 0. 0. 5. 3. 5. 4. 3. 3. 0. 4. 5. 5. 0. 0. 3. 3. 0. 4. 2. 3. 2. 5. 4.
 2. 2. 4. 1. 2. 2. 4. 1. 1. 1. 1. 1. 0. 1. 0. 1. 0. 0. 0. 1. 1. 0. 0. 0.
 0. 1. 1. 0. 0. 0. 1. 0. 0. 0. 0. 1. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]

[5. 2. 3. 4. 0. 1. 1. 2. 5. 1. 3. 4. 1. 2. 0. 4. 2. 3. 3. 1. 4. 3. 3. 5.
 0. 5. 4. 2. 4. 2. 1. 0. 0. 5. 5. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 1.
 1. 1. 0. 1. 0. 0. 1. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 1. 0. 0.]

（2）初始子代

[5. 0. 0. 5. 3. 5. 4. 3. 3. 0. 4. 5. 5. 0. 0. 3. 3. 0. 4. 2. 3. 2. 5. 4.
 2. 2. 4. 2. 4. 2. 1. 0. 0. 5. 5. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 1.
 1. 1. 0. 1. 0. 0. 1. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 1. 0. 0.]

（2）子代相比父代缺少的工序和多余工序的位置

[2.0, 1.0, 1.0, 1.0, 1.0, 1.0]
[25, 31, 32, 33, 34, 35]

（3）缺失工序替代多余工序

[5. 0. 0. 5. 3. 5. 4. 3. 3. 0. 4. 5. 5. 0. 0. 3. 3. 0. 4. 2. 3. 2. 5. 4.
 2. 2. 4. 2. 4. 2. 1. 1. 1. 1. 1. 1. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 1.
 1. 1. 0. 1. 0. 0. 1. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 1. 0. 0.]

变异

class GA(object):
    def __init__(self,chrom_size,cross_rate,mutate_rate,pop_size,job_nb,op_nb):
        self.chrom_size = chrom_size # 染色体长度
        self.cross_rate = cross_rate # 交叉概率
        self.mutate_rate = mutate_rate # 变异概率
        self.pop_size = pop_size # 种群大小
        self.pop = np.zeros((pop_size,2 * chrom_size)) # 初始种群编码
        self.job_nb = job_nb # 作业数
        self.op_nb = op_nb # 每个作业的操作数

# 编码
    def encode(self):
        number = [self.op_nb] * self.job_nb  # 每个作业的操作数
        for j in range(self.pop_size):
            numbertemp = number.copy()  # 一定要用copy!否则number也会变化
            for i in range(self.chrom_size):
                val = np.random.randint(self.job_nb)  # 随机选择作业val分配
                while numbertemp[val] == 0:  # 如果作业val的操作已经安排完，则重新选择作业分配
                    val = np.random.randint(self.job_nb)
                self.pop[j, i] = val  # 编码中记录上作业val的序号
                numbertemp[val] = numbertemp[val] - 1  # 作业val的操作数减1
                temp = machine_mat[self.op_nb - numbertemp[val] - 1, val]  # 找到作业val当前操作对应的机器
                size_temp = len(temp)
                self.pop[j, i + self.chrom_size] = np.random.randint(size_temp)
        return self.pop

# 解码
    def decode(self,pop_new):
        seq = []
        for i in range(self.pop_size):
            chrom = pop_new[i]
            chrom_op = chrom[:self.chrom_size]  # 获取操作编码
            temp = np.zeros(self.job_nb)  # 记录作业出现次数即操作编号
            p = np.zeros(self.chrom_size)  # 三位数，301表示作业3的第一个操作
            for i in range(self.chrom_size):
                job = int(chrom_op[i])  # 获取操作编码中的作业编号
                temp[job] = temp[job] + 1  # 作业job的操作编号加一
                p[i] = (job + 1) * 100 + temp[job]  # 单个操作编码成三位数
            seq.append(p)
        return np.stack(seq)

# 完工时间（适应度函数）
    def caltime(self,seq, machine_nb, process_mat, machine_mat,pop_new):
        makespan = []
        machine_number = []
        for i in range(self.pop_size):
            chrom = pop_new[i]
            chrom_ma = chrom[self.chrom_size:]  # 机器编码
            TM = np.zeros(machine_nb)  # 机器当前时间
            TP = np.zeros(job_nb)  # 作业当前时间
            m_list = np.zeros(self.chrom_size)
            Pval = np.zeros((2, self.chrom_size))  # 记录每个工序的开始时间和结束时间
            for k in range(self.chrom_size):
                job, op = divmod(int(seq[i][k]), 100)  # 获取作业和操作编号(job,op)
                index = int(chrom_ma[k])  # op对应的机器编码
                ma = machine_mat[op-1,job-1][index]  # 该操作选择的加工机器ma
                m_list[k] = ma
                pt = process_mat[op-1, job-1][index]  # 该操作的选择机器上的加工时间pt
                TMval = TM[ma-1]  # 机器ma完成当前op的时间点
                TPval = TP[job-1]  # 作业job上一道工序完成时间点
                if TMval > TPval:  # 判断机器先可用还是上一道操作先完成
                    val = TMval
                else:
                    val = TPval
                Pval[0, k] = int(val)  # 开始时间点
                Pval[1, k] = int(val) + pt  # 完工时间点
                TM[ma-1] = Pval[1, k]  # 更新机器ma的时间
                TP[job-1] = Pval[1, k]  # 更新作业job的时间
            makespan.append(Pval)
            machine_number.append(m_list)
        return np.stack(makespan),np.stack(machine_number)

# 选择
    def select(self,makespan,pop_new):
        fitness = np.max(makespan[:,1],axis=1)
        max_fitness = np.max(fitness)
        for i in range(len(fitness)):
            fitness[i] = max_fitness - fitness[i] # 调度方案最大完工时间越小，适应度越大
        # 选择保留个体的索引
        index = np.random.choice(np.arange(self.pop_size),size=self.pop_size,replace=True,p=fitness/fitness.sum()) 
        return pop_new[index]

# 交叉
    def cross(self,cross_rate,father,pop_new):
        if np.random.rand() < cross_rate:
            mother_index = np.random.randint(self.pop_size)
            mother = pop_new[int(mother_index)] # 随机选择另一个个体进行交叉
            #print('mother:{}'.format(mother))
            pos = int(np.random.default_rng(12345).integers(0, self.chrom_size, 1)) # 交叉位置
            global child
            child = np.concatenate((father[:pos], mother[pos:])) # 新个体
            #print("before:{}".format(child))
            child_sub, father_sub = copy.deepcopy(child), copy.deepcopy(father) # 用于调整工序
            for i in range(0, total_op_nb): # father_sub和child_sub分别记录了子代相比父代多余和缺少的操作
                try:
                    # index函数找不到索引会报错，因此需要使用try except
                    inx = list(father_sub).index(child_sub[i]) 
                    if inx < total_op_nb:
                        father_sub[inx] = -1
                        child_sub[i] = -1
                except ValueError as e:
                    pass
            fa_record = []  # 记录缺失的值
            ch_record = []  # 记录多余值的位置
            for i in range(total_op_nb):
                if father_sub[i] != -1:
                    fa_record.append(father_sub[i])
                if child_sub[i] != -1:
                    ch_record.append(i)
            for count in range(len(fa_record)):
                child[int(ch_record[count])] = fa_record[count] # 将child中多余的操作更改为缺失的操作
        return child

# 变异
    def mutate(self, parent,mutate_rate):
        for point in range(self.chrom_size):
            if np.random.rand() < mutate_rate:
                swap_point = np.random.randint(0, self.chrom_size) # 随机变异点
                swapA, swapB = parent[point], parent[swap_point]
                parent[point], parent[swap_point] = swapB, swapA # 对换作业和机器顺序
                swapA_ma, swapB_ma = parent[point + self.chrom_size], parent[swap_point + self.chrom_size]
                parent[point + self.chrom_size], parent[swap_point + self.chrom_size] = swapB_ma, swapA_ma
        return parent

合法个体

交叉变异后存在机器编码不合理的染色体，需要进行修正

import random

class legal(object):
    def __init__(self,chrom_size,job_nb):
        self.chrom_size = chrom_size
        self.job_nb = job_nb

    def random_index(self, rate): # 按照概率返回随机数
        start = 0
        index = 0
        max_time = max(rate)
        rate = list(map(lambda x:max_time + 1 -x,rate))
        randnum = random.randint(1, sum(rate))
        for index, scope in enumerate(rate):
            start += scope
            if randnum <= start:
                break
        return index

    def legal_solution(self, solution): # 交叉变异后的染色体中机器编码部分可能存在索引超出范围
        count = np.zeros(self.job_nb, dtype=int)
        for i in range(self.chrom_size):
            job_val = int(solution[i])
            op_val = count[job_val]
            count[job_val] += 1
            size = len(machine_mat[op_val, job_val])
            if size == 1:
                ma = 0
            else: # 按照加工时间大小选择机器
                ma = self.random_index(list(process_mat[op_val,job_val]))
                # if size < solution[i + self.chrom_size] + 1:
                # ma = np.random.randint(size)
                # solution[i + self.chrom_size] = ma
            solution[i + self.chrom_size] = ma # 修改机器编码
        return solution

绘图

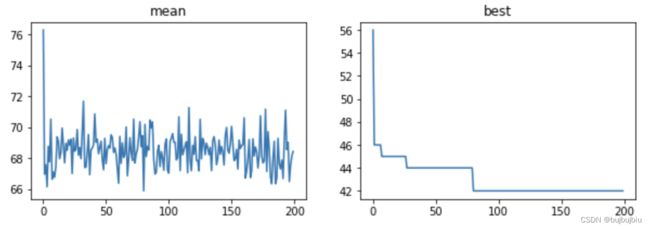
def plot(mean_ct,best_ct):
    plt.figure(figsize=(10,3))
    plt.subplot(121)
    plt.title('mean')
    plt.plot(mean_ct)
    plt.subplot(122)
    plt.title('best')
    plt.plot(best_ct)
    plt.show()

主函数

GA_JSP = GA(total_op_nb,cross_rate,mutate_rate,pop_size,job_nb,op_nb)
init_pop = GA_JSP.encode()
pop_new = init_pop
legal = legal(chrom_size=total_op_nb,job_nb=job_nb)
best_ct = 999999
mean_list = []
min_list = []
for gen in range(maxgen):
    de_pop = GA_JSP.decode(pop_new)
    makespan,machine = GA_JSP.caltime(de_pop,machine_nb,process_mat,machine_mat,pop_new)
    fitness = np.max(makespan[:,1],axis=1)
    if best_ct > np.min(fitness):
        best_ct = np.min(fitness)
        best_index = np.argmin(fitness)
        best_se = pop_new[best_index]
        best_pt = makespan[best_index]
        best_ma = machine[best_index]
    mean_list.append(np.mean(fitness))
    min_list.append(best_ct)
    select_pop = GA_JSP.select(makespan,pop_new)
    pop_copy = select_pop
    for i in range(GA_JSP.pop_size):
        new = GA_JSP.cross(cross_rate,pop_copy[i],pop_copy)
        new = GA_JSP.mutate(new,mutate_rate)
        new = legal.legal_solution(new)
        select_pop[i] = new
    pop_new = select_pop
plot(mean_list,min_list)
print(best_ct,best_index)
print('best se:{}'.format(best_se))
print('best pt:{}'.format(best_pt))
print('best ma:{}'.format(best_ma))

结果

经过200次迭代后找到的最优解如下，完工时间为42（书中最优解为47）

42.0 84
best se:[3. 1. 5. 5. 2. 0. 0. 3. 1. 3. 2. 0. 2. 5. 4. 1. 5. 0. 2. 3. 5. 4. 1. 3.
 4. 1. 2. 0. 1. 0. 2. 4. 5. 4. 3. 4. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.
 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 1. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0. 0.]
best pt:[[ 0.  0.  6.  8.  0.  1.  4.  7.  6. 14. 12. 14. 17. 12.  0. 14. 21. 23.
  22. 23. 22.  6. 18. 27. 18. 27. 27. 28. 30. 31. 41. 25. 27. 33. 28. 38.]
 [ 7.  6.  8. 12.  1.  4. 14. 10. 14. 18. 17. 23. 22. 21.  6. 15. 22. 28.
  27. 26. 27. 18. 24. 28. 25. 30. 36. 31. 33. 41. 42. 33. 30. 38. 31. 42.]]
best ma:[4. 2. 2. 4. 3. 3. 1. 9. 3. 3. 4. 2. 6. 9. 5. 5. 1. 4. 1. 2. 5. 7. 7. 5.
 3. 1. 2. 8. 4. 5. 5. 9. 3. 1. 6. 4.]

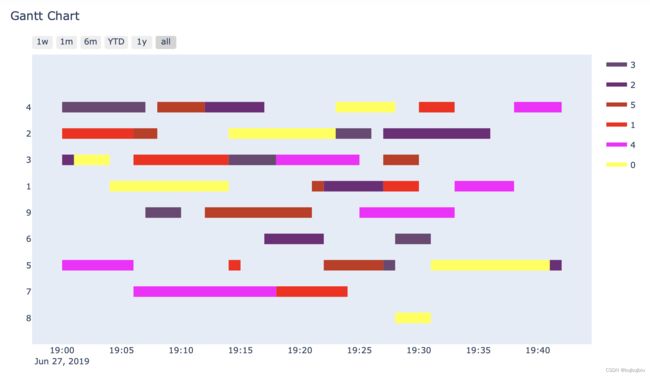
甘特图

create_gantt用法见python绘制作业车间甘特图（plotly库之create_gantt和timeline）

task = list(best_ma.astype(int))
start = list(best_pt[0].astype(int))
finish = list(best_pt[1].astype(int))
resource = list(best_se[:36].astype(int))

import pandas as pd

Resource = pd.Series(resource)
Task = pd.Series(task)
Start = pd.Series(start)
Finish = pd.Series(finish)

df = pd.DataFrame(list(zip(Task,Start,Finish,Resource)))
df.columns = ['Task','Start','Finish','Resource']

datetime = pd.Timestamp('20190627 19:00:00')
for i in range(len(df)):
    df['Start'].loc[i] = datetime + pd.Timedelta(minutes = df['Start'].loc[i])
    df['Finish'].loc[i] = datetime + pd.Timedelta(minutes = df['Finish'].loc[i])

df['Resource'] = df['Resource'].astype(str)

from plotly.express import timeline
from plotly.figure_factory import create_gantt

colors = ('rgb(46, 137, 205)',
          'rgb(114, 44, 121)',
          'rgb(198, 47, 105)',
          'rgb(58, 149, 136)',
          'rgb(107, 127, 135)',
          'rgb(46, 180, 50)')

fig = create_gantt(df,colors=['rgb(200,50,25)',(1,0,1),'#6c4774','rgb(114, 44, 121)','rgb(255,0,0)',(1,1,0.2)],
                   index_col = 'Resource',reverse_colors=True,show_colorbar=True,group_tasks = True)
fig.show()