【小波神经网络】基于小波神经网络的短时能量分析
1.软件版本
matlab2013b
2.本算法理论知识
随着计算机网络的迅速发展,目前的网络规模极为庞大和复杂,因此发生各种问题的可能性也越来越大,使管理网络的难度也增大。传统的网络管理是在告警之后,解决潜在的问题,即为一种响应式的行为,这时候网络服务很可能己经受到影响。如果在网络Qos管理和流量工程中,能够根据实际采集的网络流量观测值序列,建立该流量参数的正常行为,然后平稳化该序列,建立网络流量预测模型,对网络流量进行预测,并检测在将来超越阈值的可能性和发生时间。这样,在网络过载发生之前,可以预先采取防范措施,来保证网络的正常服务。所以研究较好的网络流量预测模型,并分析其性能,以及研究网络流量预测的实际应用,就显得尤为重要。
小波变换是近十几年信信号处理领域研究的一个热点,许多学者将小波在理论上的研究成果应用到诸如图像压缩、特征提取、信号滤波和数据融合等方面,而且小波变换的领域还在不断地发展当中。小波之所以在信号处理领域具有很大的优势,在于小波变换可以获得信号的多分辨率描述,这种描述符合人类观察世界的一般规律,同时,小波变换具有丰富的小波基以适应具有不同特性的信号。小波神经网络的基本结构如下所示:
基于小波的人工神经网络,即小波神经网络(WNN)是对生物神经进行仿真研究的结果,是基于生物学中的神经网络的基本原理,按照控制工程的思路和数学描述的方法建立起来的数学模型。WNN能够模拟人脑的结构与功能机制,实现某方面的功能,能自我感知,自主适应,有很强的学习和逼近功能;能比较准确地揭示非线性复杂动力系统的内在关系和演化机理。所以WNN可以用来分析和预测网络流量行为和演化趋势。
在实际应用中,选择小波主要从小波的对称性、正则性、支撑长度、消失矩等性质方面考虑。对称性主要用于图像处理中,对称性好的小波在进行二维图像处理中可以避免相移,简化计算;消失矩阶数大的小波变换能量更集中,在压缩中用处很大;正则性则主要用来刻画函数的光滑程度,一般正则性好的小波函数光滑性也越好,能够获得更好的重构信号;支撑长度一般与消失矩和正则性相关,支撑长度越长,消失矩和正则性也越高,但支集太长会发生边界问题,支集太短则不利于信号能量的集中。
小波函数具有不同的族系,常见的有:haar小波、Meyer小波、dbN系列小波、symN系列小波、coifN系列小波。不同的小波函数具有不同的特性,对同一信号的处理效果也不同。Haar小波是小波分析发展过程中用的最早的小波,也是最简单的小波,一般只用来理解小波分析的原理,不用于分析实际问题;Meyer小波不具有紧支性,所以在进行离散小波变换时不存在快速算法,但由Meyer小波构造的滤波器具有很高的消失矩;dbN系列小波、symN系列小波、coifN系列小波都是由DaubechieS提出来的具有紧支性的正交小波系,三种小波系相比,SymN小波类似于dbN小波,但它具有更好的对称性,而coifN小波具有更长的支撑长度和更大的消失矩,对称性也比较好。
为了达到对短时交通流数据的预测要求,为实时交通控制、诱导作准备,在对原始数据进行小波分解时既要最大限度地保留原始数据信息,使其可以为将来挖掘数据信息提供较大的灵活度,又要能够有效地辨识原始数据中的随机误差,将交通信号与噪声信号分离。
从小波分解与重构的角度来说,如果分解深度过小,近似信号会包含过多的干扰信号,导致难以确定流量变化的趋势;如果分解深度过大,滤波器频带过低,反映变化趋势的信息就会随着分解次数的增加被作为干扰信号过滤掉。因此,小波分解层数N对小波分析的效果有着重要影响。对于经过小波分解得到的信号概貌或细节成分,由香农采样定理可知,采样频率必须大于信号频率的两倍才能够获得信号中的有效信息,去除噪声。本文借鉴利用小波变换方法进行数据集成的思想,来确定小波的分解层数。
3.部分源码
clc;
clear;
close all;
%总流量数据,有效流量数据,垃圾信息流量以及病毒流量数据
[data01,data02,data03,data04,data05,data06,data07] = data_load2();
%% 总流量数据
input(:,1)=data01(:,1);
input(:,2)=data02(:,1);
input(:,3)=data03(:,1);
input(:,4)=data04(:,1);
input(:,5)=data05(:,1);
input(:,6)=data06(:,1);
output =data07(:,1);
[ynn,error]=wavelet_func(input,output,input,output);
%结果分析
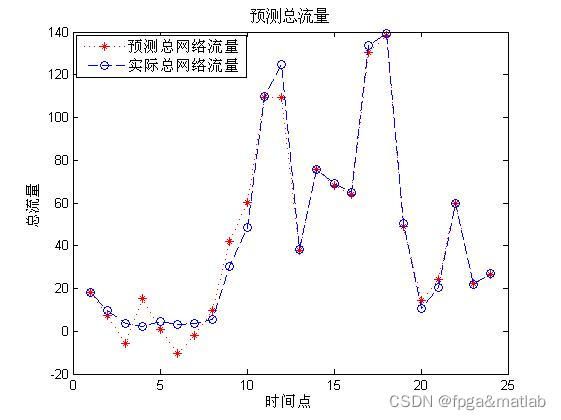
figure;
plot(ynn,'r*:')%画图
hold on
plot(output,'bo--')%画图
title('预测总流量','fontsize',12)
legend('预测总网络流量','实际总网络流量')
xlabel('时间点')
ylabel('总流量')
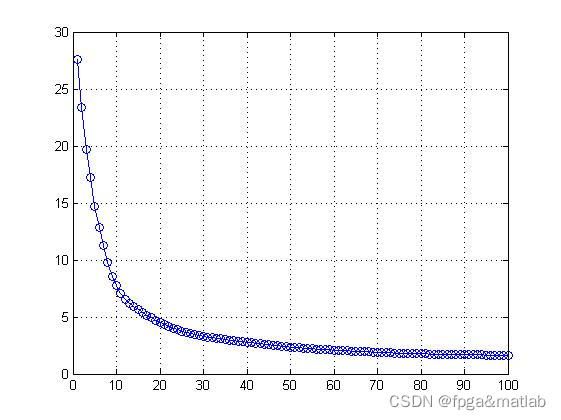
figure;
plot(error,'b-o');grid on;
figure;
plot(ynn'-output,'b-o');
%% 有效流量数据
input2(:,1)=data01(:,2);
input2(:,2)=data02(:,2);
input2(:,3)=data03(:,2);
input2(:,4)=data04(:,2);
input2(:,5)=data05(:,2);
input2(:,6)=data06(:,2);
output2 =data07(:,2);
[ynn2,error2]=wavelet_func(input2,output2,input2,output2);
%结果分析
figure;
plot(ynn2,'r*:')%画图
hold on
plot(output2,'bo--')%画图
title('预测有效流量','fontsize',12)
legend('预测有效流量','实际有效流量')
xlabel('时间点')
ylabel('有效流量')
figure;
plot(error2,'b-o');grid on;
figure;
plot(ynn2'-output2,'b-o');
%% 垃圾信息流量
input3(:,1)=data01(:,3);
input3(:,2)=data02(:,3);
input3(:,3)=data03(:,3);
input3(:,4)=data04(:,3);
input3(:,5)=data05(:,3);
input3(:,6)=data06(:,3);
output3 =data07(:,3);
[ynn3,error3]=wavelet_func(input3,output3,input3,output3);
%结果分析
figure;
plot(ynn3,'r*:')%画图
hold on
plot(output3,'bo--')%画图
title('预测垃圾信息流量','fontsize',12)
legend('预测垃圾信息流量','实际垃圾信息流量')
xlabel('时间点')
ylabel('垃圾信息流量')
figure;
plot(error3,'b-o');grid on;
figure;
plot(ynn3'-output3,'b-o');
%% 病毒流量数据
input4(:,1)=data01(:,4);
input4(:,2)=data02(:,4);
input4(:,3)=data03(:,4);
input4(:,4)=data04(:,4);
input4(:,5)=data05(:,4);
input4(:,6)=data06(:,4);
output4 =data07(:,4);
[ynn4,error4]=wavelet_func(input4,output4,input4,output4);
%结果分析
figure;
plot(ynn4,'r*:')%画图
hold on
plot(output4,'bo--')%画图
title('预测病毒流量流量','fontsize',12)
legend('预测病毒流量流量','实际病毒流量流量')
xlabel('时间点')
ylabel('病毒流量流量')
figure;
plot(error4,'b-o');grid on;
figure;
plot(ynn4'-output4,'b-o');
%%
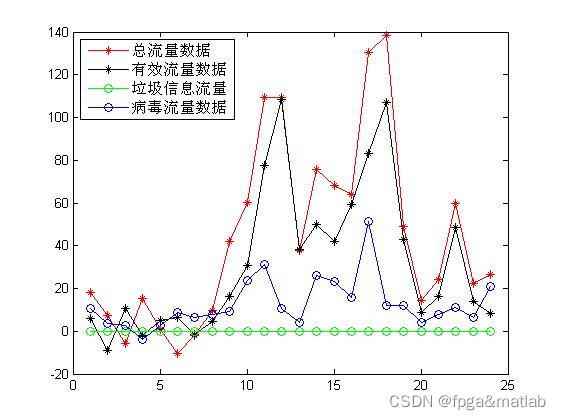
figure
plot(ynn,'r-*');hold on;
plot(ynn2,'k-*');hold on;
plot(ynn3,'g-o');hold on;
plot(ynn4,'b-o');hold off;
legend('总流量数据','有效流量数据','垃圾信息流量','病毒流量数据')
4.仿真结论
5.参考文献
[1]金旗,裴昌幸,朱畅华.ARJMA模型法分析网络流量.西安电子科技大学学报(自然科学版).2003.
[2]王立,李增智.业务管理网结构和概念模型的研究与实现.西安交通大学学报.2003.
[3]邹柏贤,刘强.基于ARMA模型的网络流量预测.计算机研究与发展.2002.A17-01