union-find并查集
#Union-Find并查集#
简介
并查集是用于解决动态连通性类问题的一种数据结构
- 什么是动态连通性(图的连通性)问题
涉及两个函数
- find(p,q)
- union(p,q)
- find(p,q)
- find用于判断图的两个节点是否连通
union用于将图的两个节点连接
Union-Find的实现
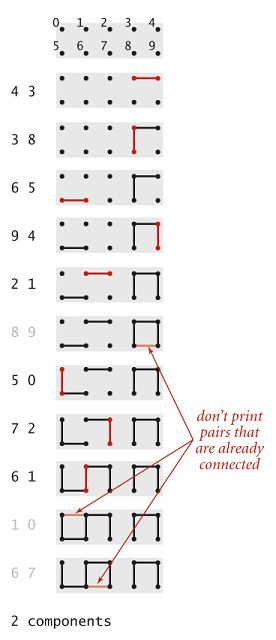
- 将图以数组形式储存,初始状态数组元素的值等于下标
连通的节点被称为一个组
Quick-Find实现
- find(p,q):直接判断数组内容,若p==q,则连通
- union(p,q):遍历数组,将值和array[q]相等的元素的值改为array[p]
- Quick-Find实现中,find十分高效,达到了O(1)的复杂度,但Union由于需要遍历数组,复杂度为O(N),若进行M次union操作,复杂度为O(MN),对于规模较大的问题,会产生性能问题
- find(p,q):直接判断数组内容,若p==q,则连通
def find(a,b):
if arr[a] == arr[b]:
print("YES")
else:
print("NO")
def union(a,b):
for i in range(arrsize):
if i == b:
continue
if(arr[i] == arr[a]):
arr[i] = arr[b]
arr[a] = arr[b]
Quick-Union实现
上面的Quick-find实现在规模增大时,会面临性能问题,其主要来源是union操作需要遍历数组,为了改善性能,需要避免执行union操作时遍历数组,Quick-Union实现达到了这一目的- Quick-Union实现中,所有节点被视为一个森林,初始状态下,每个节点都是自己所在树的根节点,执行union操作时,只需要将待连接的元素所在树的根节点连接到另一待连接元素所在树的根节点即可,执行find操作时,只要判断两个元素是否处于同一颗树上,若两元素位于同一颗树上,则两节点连通,反之不连通
- 但当执行union的对象为一组有序数对,即Quick-Union的最坏情况,树的高度将等于元素的数量,执行find操作时,如对象是树最下层的两个元素,获取每个元素的根节点都需要遍历树,则find的最坏时间复杂度为O(N^2)
- Quick-Union实现中,所有节点被视为一个森林,初始状态下,每个节点都是自己所在树的根节点,执行union操作时,只需要将待连接的元素所在树的根节点连接到另一待连接元素所在树的根节点即可,执行find操作时,只要判断两个元素是否处于同一颗树上,若两元素位于同一颗树上,则两节点连通,反之不连通
def root(a):
i = a
while(arr[i] != i):
i = arr[i]
return i
def find(a,b):
if (root(a) == root(b)):
print("YES")
else:
print("NO")
def union(a,b):
arr[root(a)] = root(b)
加权的Quick-Union实现
Quick-Union实现中,最坏情况的时间复杂度为O(N^2),最坏情况即树的高度最高,等于元素数量总和,要进一步改善Quick-Union的性能,需要限制树的最大高度
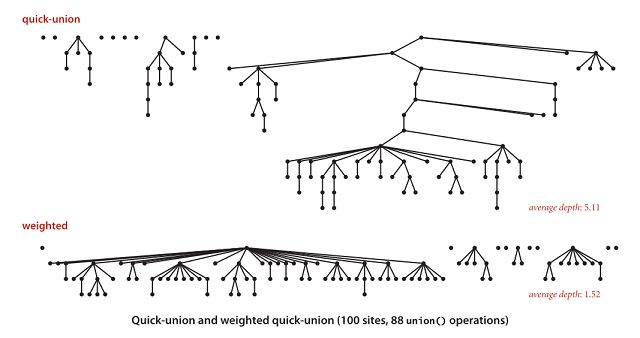
- 加权的Quick-Union实现中,union操作进行少许改变,不再规定两个待连接元素的隶属关系,而改为由两元素所在树的大小来进行判断,注意这儿是说树的大小,即树中元素数量,而非树的高度,当然是用树的高度进行判断也可以达到类似效果
- 可以证明,森林中大小为k的树的高度最多为lgk,因此最坏情况下,树的最大高度为lgN
- 加权Quick-Union实现在处理N个节点M次连接时,时间复杂度为O(MlgN)
- 加权的Quick-Union实现中,union操作进行少许改变,不再规定两个待连接元素的隶属关系,而改为由两元素所在树的大小来进行判断,注意这儿是说树的大小,即树中元素数量,而非树的高度,当然是用树的高度进行判断也可以达到类似效果
def root(a):
i = a
while(arr[i] != i):
i = arr[i]
return i
def find(a,b):
if (root(a) == root(b)):
print("YES")
else:
print("NO")
def union(a,b):
if sz[root(a)] < sz[root(b)]:
sz[root(b)] += sz[root(a)]
arr[root(a)] = root(b)
else:
sz[root(a)] += sz[root(b)]
arr[root(b)] = root(a)
带路径压缩的加权Quick-Union
- 目的是将所有节点直接连接到根节点上,进一步优化时间,实现很简单,在执行find时,每次遇到的节点都连接到其祖父节点上,这样可以进一步减小树的高度,优化时间复杂度
def root(a):
i = a
while(arr[i] != i):
i = arr[i]
return i
def find(a,b):
if (root(a) == root(b)):
arr[a] = arr[root(a)]
print("YES")
else:
print("NO")
def union(a,b):
if sz[root(a)] < sz[root(b)]:
sz[root(b)] += sz[root(a)]
arr[root(a)] = root(b)
else:
sz[root(a)] += sz[root(b)]
arr[root(b)] = root(a)

应用
Social network connectivity. Given a social network containing N members and a log file containing M timestamps at which times pairs of members formed friendships, design an algorithm to determine the earliest time at which all members are connected (i.e., every member is a friend of a friend of a friend ... of a friend). Assume that the log file is sorted by timestamp and that friendship is an equivalence relation. The running time of your algorithm should be MlogN or better and use extra space proportional to N.
宝典P231:假如已知n个人和m对好友关系(存于数组r),若两个人是直接或间接的好友,则认为他们属于同一个朋友圈,请写程序求出这n个人里一共有多少个朋友圈,并分析代码的时间、空间复杂度
- 同一类型的并查集应用,题1的时间戳,题2的好友关系数组r用于执行union操作,使用加权的并查集算法可以获得O(MlgN)的时间复杂度,使用带路径压缩的并查集算法可以获取O(N)的时间复杂度,第一题即第二题的延伸,当所有好友都连通的时候,即符合第一题条件
- python实现
friends = []
size = []
def root(a):
i = a
while(friends[i] != i):
i = friends[i]
return i
def find(a, b):
if(root(a) == root(b)):
friends[a] = friends[friends[a]]
return True
return False
def union(a, b):
i = root(a)
j = root(b)
if(size[i] < size[j]):
size[j] += size[i]
friends[i] = j
else:
size[i] += size[j]
friends[j] = i
def cntset():
setcnt = 0
for i in range(peoplecnt):
if(friends[i] == i):
setcnt += 1
return setcnt
peoplecnt = int(raw_input("Input Number of people:"))
for i in range(peoplecnt):
friends.append(i)
size.append(1)
while True:
a = int(raw_input("Input a:"))
b = int(raw_input("Input b:"))
if(a == -1 | b == -1):
break;
else:
union(a,b)
print(cntset())
Union-find with specific canonical element. Add a method find() to the union-find data type so that find(i) returns the largest element in the connected component containing i. The operations, union(), connected(), and find() should all take logarithmic time or better.
For example, if one of the connected components is {1,2,6,9}, then the find() method should return 9 for each of the four elements in the connected components.
- 增加一个新的数组max,森林中每棵树的根节点对于的元素中储存这棵树中最大的元素,每次执行union操作时,检查max并更新即可
Successor with delete. Given a set of N integers $S={0,1,...,N−1} $and a sequence of requests of the following form:
Remove $x$ from $S$
Find the successor of$ x$: the smallest $y$ in $S$ such that $y≥x$.
design a data type so that all operations (except construction) should take logarithmic time or better.
- S是一个有序的序列,这是采用并查集解决这个问题的基础,从S中删除一个元素S[i],由于S有序,将S[i]和S[i+1]连接,这样就有了一个组。组中最大的元素是序列中尚未被删除的一个元素,即successor of x,仅当删除的是S的最后一个元素时不存在符合要求的元素。配合上题的寻找每个组中最大元素的方法,即可求解
- python的一个小坑,如果不是基础类型,所有=都是引用,数组复制使用 b = a * 1或b = [i for i in a]
- max element和successor的python实现
arr = [0,1,2,3,4,5,6,7,8,9]
sz = [1,1,1,1,1,1,1,1,1,1]
maxe = [i for i in arr]
def root(a):
i = a
while(arr[i] != i):
i = arr[i]
return i
def find(a,b):
if (root(a) == root(b)):
arr[a] = arr[root(a)]
print("YES")
else:
print("NO")
def union(a,b):
i = root(a)
j = root(b)
if sz[i] < sz[j]:
sz[j] += sz[i]
maxe[j] = max(maxe[j], maxe[i])
arr[i] = j
else:
sz[i] += sz[j]
maxe[i] = max(maxe[j], maxe[i])
arr[j] = i
print("Array size 10, index from 0~9")
while 1:
x = int(raw_input("input index to delete"))
if x == 9:
print("9 is max in the sequence, no successor")
else:
union(x, x+1)
print("successor of " + str(x) + " is " + str(maxe[root(x)]))
Written with StackEdit.