生存分析的一些整理笔记

生存分析是研究生存时间的分布规律，以及生存时间和相关因素之间关系的一种统计分析方法
一、生存分析
1、生存分析的三个研究内容：

• 生存描述-描述不同时间的总体生存率，计算中位生存时间，绘制生存函数曲线，一般用Kaplan-Meier方法和寿命表法；
• 生存曲线比较-比较不同处理组的生存率，一般用logrank检验；
• 生存相关因素的分析：回归模型；由于logrank检验仅能分析一个因素，因此两个或者两个以上因素的分析需要使用Cox比例风险模型；

2、生存分析使用的方法：

• Kaplan-Meier plots to visualize survival curves（根据生存时间分布，估计生存率以及中位生存时间，以生存曲线方式展示，从而分析生存特征，一般用Kaplan-Meier法，还有寿命法）
• Log-rank test to compare the survival curves of two or more groups（通过比较两组或者多组之间的的生存曲线，一般是生存率及其标准误，从而研究之间的差异，一般用log rank检验）
• Cox proportional hazards regression to describe the effect of variables on survival（用Cox风险比例模型来分析变量对生存的影响，可以两个及两个以上的因素，很常用）
  所以一般做生存分析，可以用KM（Kaplan-Meier）方法估计生存率，做生存曲线，然后可以根据分组检验一下多组间生存曲线是否有显著的差异，最后用Cox风险比例模型来研究下某个因素对生存的影响

3、基本术语：

• Event（事件）：在癌症研究中，事件可以是Relapse，Progression以及Death
• Survival time（生存时间）：一般指某个事件的开始到终止这段事件，如癌症研究中的疾病确诊到缓解或者死亡，其中有几个比较重要的肿瘤临床试验终点：
  – OS（overall survival）：指从开始到任意原因死亡的时间，我们一般见到的5年生存率、10年生存率都是基于OS的

总生存期（Overall survival，OS）指的是从病人确认患有疾病开始至因任何原因引起死亡的时间。该指标常常被认为是肿瘤临床试验中最佳的疗效终点。确认病人因病或其他因素引起死亡的日期通常几乎没有困难，并且死亡的时间有其独立的因果关系。如果在生存期上有小幅度的提高，可以认为是有意义的临床受益证据。作为一个终点，生存期应每天进行评价，可通过在住院就诊时或随访时，通过与患者直接接触或者通过电话与患者交谈来确认并进行相关记录，了解病人患病期间的生活质量和用药后各种症状的变化，了解并分析引起病人的死因。

– progression-free survival（PFS，无进展生存期）：指从开始到肿瘤发生任意进展或者发生死亡的时间；PFS相比OS包含了恶化这个概念，可用于评估一些治疗的临床效益

所谓无病进展生存期（Progression-Free Survival，PFS）通常定义为病人经过治疗，随机选择某个时间直到肿瘤复发或因各种原因出现死亡，病人总的生存时间。PFS的优点在于它能反映肿瘤的生长（这个现象可能反映了肿瘤相关疾病或死亡的因果联系），可以于生存获益证实前被评价，不会受到后续治疗的潜在的易混淆的指标或症状影响。而且PFS的结果比生存期结果出现得更早，治疗过程中，病人一旦出现了症状，肿瘤复发了，过了无病进展生存期就要采取其他积极治疗手段，从而进一步改善患者的症状，延长生存时间。PFS作为支持药品上市许可的终点指标角色随不同肿瘤而变化。在一些情况下，PFS延长可能是一个支持药品常规批准的可接受的临床获益替代终点指标，在其它情况下，它可能作为加快通过的反映临床获益的替代指标。需重点考虑的是治疗效应大小、治疗中的毒性方面、临床获益以及可利用治疗的毒性。

– time to progress（TTP，疾病进展时间）：从开始到肿瘤发生任意进展或者进展前死亡的时间；TTP相比PFS只包含了肿瘤的恶化，不包含死亡
– disease-free survival（DFS，无病生存期）：指从开始到肿瘤复发或者任何原因死亡的时间；常用于根治性手术治疗或放疗后的辅助治疗，如乳腺癌术后内分泌疗法等：
– event free survival（EFS，无事件生存期）：指从开始到发生任何事件的时间，这里的事件包括肿瘤进展，死亡，治疗方案的改变，致死副作用等（主要用于病程较长的恶性肿瘤、或该实验方案危险性高等情况下）
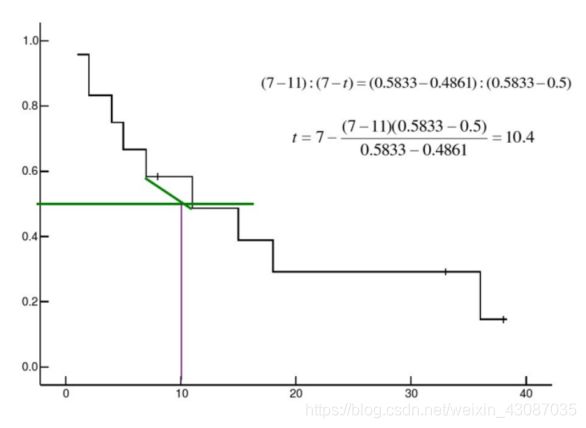
– 中位生存期（Median Survival Time，MST）又称半数生存期，即当累积生存率为50%时所对应的生存时间，表示有且只有50%的生病个体可以活过这个时间。通俗地讲，就是指病人经过某种药物或治疗手段治疗时，只剩下一半（50%）的病人的生存时间。如果有9个病人（奇数），按生存期从短到长排列，第5个病人的生存时间就是中位生存时间；如果有10个病人（偶数），按生存期从短到长排列，第5、6个病人的生存时间就是中位生存时间。

• Censoring（删失）：这经常会在临床资料中看到，生存分析中也有其对应的参数，一般指不是由死亡引起的的数据丢失，可能是失访，可能是非正常原因退出，可能是时间终止而事件未发等等，一般在展示时以‘+’号显示
  – left censored（左删失）：只知道实际生存时间小于观察到的生存时间
  – right censored（右删失）：只知道实际生存时间大于观察到的生存时间
  – interval censored（区间删失）：只知道实际生存时间在某个时间区间范围内
• 失效事件（Failure Event）：常被简称为事件，研究者规定的终点结局，医学研究中可以是患者死亡，也可以是疾病的发生、某种治疗的反应、疾病的复发等。与之对应的起始事件可以是疾病的确诊、某种治疗的开始等。
• 生存时间（Survival Time）：常用t表示，从规定的起始事件开始到失效事件出现所持续的时间。对于失访者，是失访前最后一次随访的时间。
• 删失/截尾（Censoring）：由于某些原因在随访中并没有观测到失效事件而不知道确切的生存时间，此部分数据即删失数据。常见原因有失访、患者退出试验、事件发生是由于非研究性疾病（如研究病人发生脑卒中后的生存时间，结果病人因为车祸死亡）、研究结束时研究对象仍未发生失效事件。删失数据的生存时间为起始事件到截尾点所经历的时间。
• 生存函数（Survival Function）与风险函数（Hazard Function）：生存函数也称为积累生存函数/概率（Cumulative Survival Function）或生存率，符号S(t)，表示观察对象生存时间越过时间点t的概率，t=0时生存函数取值为1，随时间延长生存函数逐渐减小。以生存时间为横轴、生存函数为纵轴连成的曲线即为生存曲线。风险函数表示生存时间达到t后瞬时发生失效事件的概率，用h(t)表示，h(t)=f(t)/S(t)。其中f(t)为概率密度函数（Probability Density Function），f(t)是F(t)的导数。F(t)为积累分布函数（Cumulative Distribution Function），F(t)=1-S(t)，表示生存时间未超过时间点t的概率。累积风险函数H(t)=-logS(t)。本人数学很差，概率密度和积累分布的关系类似于速度与位移的关系。
• 中位生存时间（Median Survival Time）/平均生存时间（Mean Survival Time）：中位生存时间又称半数生存期，表示恰好一半个体未发生失效事件的时间，生存曲线上纵轴50%对应的时间。平均生存时间则表示生存曲线下的面积。

我们前面了解到生存分析需要计算生存率，而生存率（survival rate）则可以看作条件生存概率（conditional probability of survival）的累积，比如三年生存率则是第1-3年每年存活概率的乘积.

生存率又叫生存概率或者生存函数，表示一个病人的生存时间长于时间t的概率，用s(t)表示，s(t)=P(T≥t)，生存率曲线是一条下降的曲线；

4、生存分析的方法
一般可以分为三类：
1.参数法：知道生存时间的分布模型，然后根据数据来估计模型参数，最后以分布模型来计算生存率,参数法是求出一个函数来表示是s(t)和t的关系
2.非参数法：不需要生存时间分布，根据样本统计量来估计生存率，常见方法Kaplan-Meier法（乘积极限法）、寿命法,参数法是求出几个时间点的生存率，然后再用直线连接起来，画出的生存曲线是呈阶梯型的；
3.半参数法：也不需要生存时间的分布，但最终是通过模型来评估影响生存率的因素，最为常见的是Cox回归模型
而生存曲线（survival curve）则是将每个时间点的生存率连接在一起的曲线，一般随访时间为X轴，生存率为Y轴；曲线平滑则说明高生存率，反之则低生存率；中位生存率（median survival time）越长，则说明预后较好

中位生存时间：举个例子

简单看下Kaplan-Meier方法是怎么计算的：
S(ti)=S(ti−1)(1−di/ni)
1.S(ti−1)指在ti−1年还存活的概率
2.ni指在在ti年之前还存活的人数
3.di指在事件发生的人数
4.t0=0，S(0)=1
如果想更加通俗的了解生存率/生存曲线/乘积极限法等概念，可以看画说统计 | 生存分析之Kaplan-Meier曲线都告诉我们什么，比教科书版的解释通俗易懂多啦

二、Cox比例风险模型

从分析的因素上看，有单因素分析和多因素分析。正如“连续资料的单因素分析常用t检验、方差分析，对应的多因素分析是多重线性回归”、“分类资料的单因素分析方法卡方分析，对应的多因素分析有logistic回归”一样，生存分析的常用单因素（或少数因素）的分析有Life
Tables法、Kaplan-Meier法，对应的多因素模型则常用Cox回归模型（Cox风险比例模型）。从采取的分析方法上看，生存分析有非参数法（如Wilcoxon法、Log-rank法）、参数法（如Weibull回归、lognormal回归等）和半参数分析（Cox回归）。

Cox回归要求满足比例风险假定(proportional-hazards assumption)的前提条件。所谓比例风险假定，就是假定风险比(HR，Hazard Ratio)不随时间t变化而变化。

1、Cox模型基本知识：

h（t,X）代表当各协变量固定时的风险函数；
h(t)=lim(在时间t生存的病人死于区间（t,△t）的概率/△t)=死于区间（t,△t）的病人数/（在t时刻尚存活的病人数*△t）,h(t)叫做风险函数或者风险率；
h0(t)是基础风险函数，是全部协变量或者标准状态下的风险函数，一般是未知的；所以Cox模型又叫半参数模型；
此处注意风险函数同概率密度函数的区别：概率密度函数f(t)=lim(一个病人在区间(t,t+△t)内死亡的概率/△t)，f(t)中的分子是累积概率，而h(t)中的分子是条件概率；因此h(t)可称为生存到时间t的病人在时间t的瞬时死亡率或条件死亡概率；
当某个协变量的回归系数大于0时，该协变量是危险因素，使生存时间越短，反之则是保护因素，使生存时间越长；
RR=h(t,X)/h0(t);

模型结构与参数释义可参见颜虹等主编的《医学统计学》，如下。对此不感兴趣而只关心操作和结果解读的，可直接越过。

2、Cox模型参数估计与假设检验：
参数估计：最大似然法
假设检验：似然比检验，得分检验，Wald检验；

3、因素筛选与最优模型的建立：
变量筛选方法：向前引入法，向后剔除法，逐步引入-剔除法
因素作用大小排序：标准化回归系数的绝对值

4、Cox模型的注意事项
因素对生存时间的作用不随时间变化；因素分析时对于连续变量要考察其分布是否偏态；

未完待续…