AtLoc: Attention Guided Camera Localization 相机重定位 论文笔记
牛津大学计算机学院 2019.10
注意力是个好东西。从Atloc和AtLoc+的实验结果可以看出,自注意力机制对定位精度有大幅提升,时序约束只有略微的提升,但是时序约束增加了输入数据量延长了处理时间,还对传感器提出了更高的要求,相比之下注意力性价比高得多
在现有的基于深度学习的相机重定位的方法中,基于单目数据的方法还不够鲁棒。在一些程度上可以通过序列图像或者几何约束来剔除动态物体。本文通过实验证实了基于注意力的网络可以在单目数据上获得SOTA的性能。
由于手工特征的鲁棒性不够,传统基于手工特征描述子的相机重定位方法在室外的性能下降非常明显。
基于深度学习的方法代表之作是PoseNet,在单张图片上生成特征最后输出全局位姿。其变种的模型使用了不同的特征提取网络,或者几何约束等。但是在动态目标和动态照明的环境下鲁棒性很差,在户外数据集下尤其明显。
为了提升鲁棒性,后来的技术考虑了使用多张图像作为输入,并假定网络可以学会拒绝帧之间的不一致的特征。例如VidLoc 以及MapNet(相机位姿回归的SOTA)
本文提出了一种替代的方案实现了鲁棒的相机重定位,使用单目图像作为输入,学习专注于时间上一致且信息丰富的图像部分,例如建筑物,而忽略了动态部分例如车辆和行人。该模型为AtLoc(注意力导向的相机重定位方法),AtLoc不要求序列的输入以及几何约束作为额外信息。
实验证明AtLoc能够在一般数据集上获得SOTA的性能,甚至超越了基于双目图片的方法。在室内以及室外数据集都可以高效运行。AtLoc不需要额外的手工几何损失函数即可进行端到端的训练。
基于深度学习的相机重定位
略
注意力机制
本文工作基于自注意力机制。自注意力机制被广泛用于需要捕获长距离依赖性的模型中。设计之初是用于机器翻译,并取得了SOAT的性能。后来用于自回归模型,作为图像迁移器生成图像。另一种用法是形式化为non-local 操作,以捕获视频序列中的时空依赖性。生成对抗网络(GAN)引入了类似的non-local 体系结构,用于提取全局的远程依赖关系。(Parisotto et al.2018) 将基于注意力的递归神经网络用于SLAM系统中的后端优化。尽管自注意机制在NLP以及CV领域获得了如此巨大的成功以及广泛的应用,自注意力机制从未出现在相机位姿回归中。
论文工作将Non-local 风格的自我注意机制集成到了相机定位模型中,以展示 对鲁棒关键特征的对应以及提升模型性能的有效性。
首先通过特征提取器得到特征图,然后注意力模块在特征图上计算得到Attention map,最后位姿回归器将新的特征图映射为相机位姿。
1. 视觉编码器
负责提取特征。论文选择了ResNet34作为backbone,用IamgeNet上预训练的权重初始化。调整网络最后FCN的输出维度,并去掉用于分类的softmax层。
2. 注意力模块
与之前的尝试通过引入时间信息(Clark等人,2017)或几何约束(Brahmbhatt等人,2018)不同,论文将自注意机制纳入模型框架。注意力模块负责找出特征图中静态的、有意义的特征点,它能够自我调节,而无需任何手工设计的几何形状信息或其他先验信息。
-
特征图: X = f e n c o d e r ( I ) X=f_{encoder}(I) X=fencoder(I),
-
计算内积相似度: S ( X i , X j ) = θ ( X i ) T ϕ ( X j ) S(X_i,X_j)=\theta(X_i)^T\phi(X_j) S(Xi,Xj)=θ(Xi)Tϕ(Xj),其中 θ ( X i ) = W θ X i \theta(X_i)=W_{\theta}X_i θ(Xi)=WθXi 、 ϕ ( X j ) = W ϕ X j \phi(X_j)=W_{\phi}X_j ϕ(Xj)=WϕXj分别将位置i、j处的特征线性地映射到两个特征空间中。
-
计算归一化因子: C ( X i ) = ∑ ∀ j S ( X i , X j ) C(X_i)=\sum_{\forall_j}S(X_i,X_j) C(Xi)=∑∀jS(Xi,Xj)
-
注意力向量: Y i = 1 C ( X i ) ∑ ∀ j S ( X i , X j ) g ( X j ) Y_i=\frac{1}{C(X_i)}\sum_{\forall_j}S(X_i,X_j)g(X_j) Yi=C(Xi)1∑∀jS(Xi,Xj)g(Xj),其中 g ( X i ) = W g X j g(X_i)=W_gX_j g(Xi)=WgXj为另一个线性变换
注意力向量表示了模型在位于位置i处的特征 X i X_i Xi上 focus 的程度。
以上过程可以总结为: Y = S o f t m a x ( X T W θ T W ϕ X ) W g X Y=Softmax(X^TW_{\theta}^TW_{\phi}X)W_gX Y=Softmax(XTWθTWϕX)WgX
-
最后模型采用了残差连接的思想,在注意力输出时加入了输入数据 X X X:
A t t ( X ) = α ( Y ) + X Att(X) = \alpha(Y)+X Att(X)=α(Y)+X
其中 α ( Y ) = W α Y \alpha(Y)=W_{\alpha}Y α(Y)=WαY,该线性映射输出具有可学习权重的缩放后的自注意向量。
模型通过全连接层在空间(C / n)中生成学习的权重矩阵Wθ,Wφ,Wg和Wα,其中C是输入特征X的通道数,n是该特征到Attention map的下采样率。根据大量实验,作者发现n = 8在不同数据集上的效果最佳。
3. 相机位姿回归器
本质是一个多层感知机:
[ p , q ] = M L P s ( A t t ( X ) ) [p,q]=MLPs(Att(X)) [p,q]=MLPs(Att(X))
p是相机坐标,q是单位四元数
回归的损失函数:
L o s s ( I ) = ∣ ∣ p − p ^ ∣ ∣ 1 e − β + β + ∣ ∣ l o g q − log q ^ ∣ ∣ 1 e − γ + γ Loss(I)=||p-\hat{p}||_1e^{-\beta}+\beta+||log^q-\log^{\hat{q}}||_1e^{-\gamma}+\gamma Loss(I)=∣∣p−p^∣∣1e−β+β+∣∣logq−logq^∣∣1e−γ+γ
- 其中 β \beta β和 γ \gamma γ是位置损失和四元数损失的权重, l o g q log^q logq是 四元数的对数形式:
l o g q = { v ∣ ∣ v ∣ ∣ c o s − 1 u , i f ∣ ∣ v ∣ ∣ ≠ 0 0 , o t h e r w i s e log^q=\begin{cases} \frac{v}{||v||}cos^{-1}u,&if ||v||\not=0\\ 0,& otherwise \end{cases} logq={∣∣v∣∣vcos−1u,0,if∣∣v∣∣=0otherwise
u,v分别表示单位四元数的实部和虚部
四元数很好用但是有一个问题:四元数不是唯一的。 在实践中,两个q、q‘可以表示相同的旋转,因为单个旋转可以映射到两个半球。 为了确保每个旋转仅具有唯一的值,本文将所有四元数限制为相同的半球。
时序约束
这里借鉴了几何感知学习的思想,作者通过图像对之间的时序约束将AtLoc扩展到了AtLoc+,因为直观上,时序约束可以强制模型学习全局一致的特征,从而提高总体定位精度。
考虑了时序约束的损失函数为:
L o s s ( I t o t a l ) = L o s s ( I i ) + α ∑ i ≠ j L o s s ( I i j ) Loss(I_{total})=Loss(I_i)+\alpha\sum_{i\not=j}Loss(I_{ij}) Loss(Itotal)=Loss(Ii)+αi=j∑Loss(Iij)
i,j为图像的index, I i j ( p i − p j , q i − q j ) I_{ij}(p_i−p_j,q_i−q_j) Iij(pi−pj,qi−qj)表示图像 i j 之间的相对位姿。
Baseline:
- 单目方法:PoseNet,Bayesian PoseNet,PoseNet Spatial-LSTM,Hourglass,PoseNet17
- 时序方法: VidLoc,MapNet
户外数据集上:PoseNet+,Stereo VO,MapNet,
实验结果:
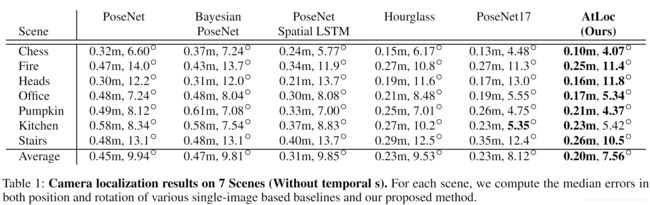
与单目方法的比较:大幅领先
时序变种模型与当前时序方法的比较:仍然领先
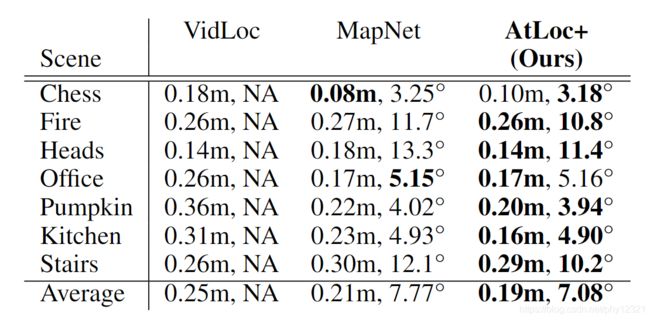
实验结果分析
通过将注意力可视化,可见AtLoc在注意力机制下更加关注具有几何意义的区域(例如关键点和直线),而不是没有特征的区域,并且随着时间的推移显示出更好的一致性
速度
MapNet:9.4ms
PoseL-STM:9.2ms
AtLoc :6.3ms
