蓝桥杯刷题-第一章 递归与递推
蓝桥杯刷题-第一章 递归与递推
-
- 1、递归与递推
-
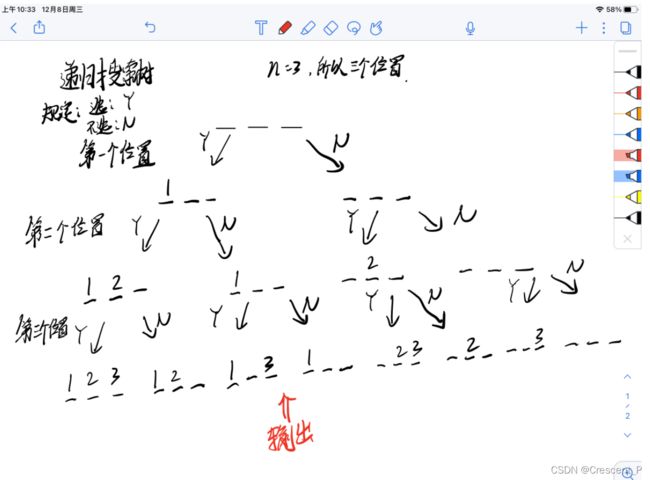
- 递归实现指数型枚举
- 递归实现排列型枚举
- 递归实现组合型枚举
- 简单的斐波那契数列
- 费解的开关
- 翻硬币
- 飞行员兄弟
- 带分数
BaseOn : https://www.acwing.com
1、递归与递推
递归实现指数型枚举
java
import java.util.*;
public class Main{
static Scanner in = new Scanner(System.in); // 输入
// 看题目范围 n是1到15,我们稍微把数组开大一点点、防止数组越界。
static int max = 20,n;
// 判断每一位是否被用过
static boolean[] st = new boolean[max];
public static void main(String[] args){
n = in.nextInt();
dfs(0);
}
// dfs(深度优先搜索)
private static void dfs(int u){
// 搜索到最后一位
if(u == n){
// 打印输出
for(int i = 0;i < n;i++){
if(st[i]) System.out.printf("%d ",i+1);
}
System.out.println();
return;
}
// 要第u位
st[u] = true;
dfs(u+1);
// 不要第u位
st[u] = false;
dfs(u+1);
}
}
C/C++
#include 递归实现排列型枚举
Java
import java.util.*;
import java.io.*;
public class Main {
static Scanner in = new Scanner(System.in);
static int max = 10, n;
static int[] path = new int[max]; // 存储路径
static boolean[] st = new boolean[max]; // 记录每个数字是否被使用了
static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args)throws Exception{
n = in.nextInt();
dfs(0);
out.flush();
}
private static void dfs(int u) throws Exception{
if(u == n){
for(int i = 0;i < n;i++) out.write(path[i] + " "); // 快速写出
out.write("\n"); // 换行
return;
}
for(int i = 0;i < n;i++){
if(!st[i]){
st[i] = true;
path[u] = i+1;
dfs(u+1);
st[i] = false;
path[u] = 0;
}
}
}
}
C/C++
#include 递归实现组合型枚举
Java
import java.util.*;
public class Main{
static Scanner in = new Scanner(System.in);
static int max = 30,n,m;
static int[] path = new int[max];
public static void main(String[] args){
n = in.nextInt();
m = in.nextInt();
dfs(0);
return;
}
public static void dfs(int u){
if(u == m){
for(int i = 0;i < m;i++) System.out.printf("%d ",path[i]);
System.out.println();
return;
}
for(int i = 1;i <= n;i++){
if(u == 0) path[u] = i;
else {
if(path[u-1] < i) path[u] = i;
else continue;
}
dfs(u+1);
}
}
}
C/C++
#include 简单的斐波那契数列
java
import java.util.*;
public class Main{
static Scanner in = new Scanner(System.in);
static int n,a = 0,b = 1;
public static void main(String[] args){
n = in.nextInt();
for(int i = 0;i < n;i++){
System.out.printf("%d ",a);
int temp = a + b;
a = b;
b = temp;
}
}
}
C/C++
#include 费解的开关
想写出这个题目,首先得分析出几个点:
- 每个灯泡只能被摁一次,因为摁两次不会有任何改变,并且还多了步数
- 摁的顺序是无所谓的,先摁哪个再摁哪个是没关系的。
依靠上面两个结论,我们来看这一题:
- 我们可以先只看第一行,第一行我们可以随意摁,但是每个灯泡只能被操作一次。
- 第一行被操作过了,轮到第二行,此时第一行如果还有灭的,只能通过第二行来将其熄灭。逻辑就是这样,下面的每一行的灯泡是否操作,都是看上一行灯灯泡的状态。
因此:
- 我们枚举第一行的所有状态
- 怎么枚举,第一行一共5个灯泡、每个灯泡开或关有两种状态、那么就是2^5=32种状态
- 之后根据当前第一行的状态去操作后续的行
- 到最后一行、看是否有开的,如果有,说明不能全灭
C/C++
#include java
import java.util.*;
public class Main{
static Scanner in = new Scanner(System.in);
static int max = 5;
static char[][] g = new char[max][max];
static char[][] backup = new char[max][max];
static int[] dx = {1,0,-1,0,0},dy = {0,1,0,-1,0};
public static void main(String[] args){
int T = in.nextInt();
// T个测试样例
while(T-- > 0){
// 读入图
int res = 10;
for(int i = 0;i < 5;i++) g[i] = in.next().toCharArray();
// 要对图进行一次备份
for(int i = 0;i < 5;i++){
for(int j = 0;j < 5;j++) backup[i][j] = g[i][j];
}
// 第一行有5个格子,每个格子开或关有2种可能,一共2^5=32种,我们这里采用二进制来表示
for(int op = 0;op < 32;op++){
int step = 0;
// 先操作第一行
for(int i = 0;i < 5;i++){
// 当前位是1就进行一次操作
if((op >> i & 1) == 1){
turn(0,i);
step++;
}
}
// 通过上一行操作下一行
for(int i = 0;i < 4;i++){
for(int j = 0;j < 5;j++){
// 当前是灭的,那么下一行对应的就要开
if(g[i][j] == '0'){
turn(i+1,j);
step++;
}
}
}
// 判断最后一行有没有灭的
boolean dark = false;
for(int i = 0;i < 5;i++){
if(g[4][i] == '0'){
dark = true;
break;
}
}
// 全灭的话
if(!dark) res = Math.min(res,step);
// 对图进行还原
for(int i = 0;i < 5;i++){
for(int j = 0;j < 5;j++) g[i][j] = backup[i][j];
}
}
// 超过步数
if(res > 6) res = -1;
// 此时已经遍历了32种情况
System.out.println(res);
}
}
public static void turn(int x,int y){
for(int i = 0;i < 5;i++){
int nx = x + dx[i],ny = y + dy[i];
if(nx < 0 || nx >= 5 || ny < 0 || ny >= 5) continue; // 出界不需要考虑
if(g[nx][ny] == '0') g[nx][ny] = '1';
else g[nx][ny] = '0';
}
}
}
翻硬币
按照之前的思考:
- 每个硬币只会主动被翻一次(因为旁边的翻动不是主动翻动)
- 翻动的顺序没有关系
对于此题:
我们可以就从左到右枚举,当前对应位不一样,就翻转一下即可。
c/c++
#include Java
import java.util.*;
import java.io.*;
public class Main{
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static int N = 110;
static char[] begin = new char[N],end = new char[N];
public static void main(String[] args)throws Exception{
int ans = 0;
// 读入
String a = in.readLine();
String b = in.readLine();
begin = a.toCharArray();
end = b.toCharArray();
for(int i = 0;i < begin.length-1;i++){
if(begin[i] != end[i]){
if(begin[i+1] == '*') begin[i+1] = 'o';
else begin[i+1] = '*';
ans++;
}
}
in.close();
System.out.println(ans);
}
}
飞行员兄弟
C/C++
#include Java
import java.util.*;
public class Main{
static int N = 4;
static char[][] g = new char[N][N],backup = new char[N][N];
static Scanner in = new Scanner(System.in);
static List<int[]> ans = new ArrayList<>();
public static void main(String[] args){
// 把图给读进来
for(int i = 0;i < 4;i++) g[i] = in.next().toCharArray();
// 一共16个开关,全部枚举,2^16
for(int op = 0;op < (1 << 16);op++){
List<int[]> temp = new ArrayList<>();
// 备份图
for(int i = 0;i < 4;i++){
for(int j = 0;j < 4;j++){
backup[i][j] = g[i][j];
}
}
// 遍历每一个点
for(int i = 0;i < 4;i++){
for(int j = 0;j < 4;j++){
// 为1就是要操作
if(((op >> get(i,j)) & 1) == 1){
turn_all(i,j);
temp.add(new int[]{i,j});
}
}
}
// 此时遍历完了,看是否全打开了
boolean has_closed = false;
for(int i = 0;i < 4;i++){
for(int j = 0;j < 4;j++){
if(g[i][j] == '+') has_closed = true;
}
}
// 没有关闭的
if(!has_closed){
if(ans.isEmpty() || ans.size() > temp.size() ) ans = temp;
}
// 复原
for(int i = 0;i < 4;i++){
for(int j = 0;j < 4;j++){
g[i][j] = backup[i][j];
}
}
}
System.out.println(ans.size());
for(int[] res : ans){
System.out.printf("%d %d\n",res[0]+1,res[1]+1);
}
}
public static int get(int x,int y){
return 4 * x + y;
}
public static void turn_all(int x,int y){
for(int i = 0;i < 4;i++){
turn_one(x,i);
turn_one(i,y);
}
turn_one(x,y);
}
public static void turn_one(int x,int y){
if(g[x][y] == '-') g[x][y] = '+';
else g[x][y] = '-';
}
}
带分数
思路一:
- 将带分数形式化为 : n = a + b / c
- 其中a、b、c 就是1~9的组合
- 再简化 就是 n * c = a * c + b
- 这样我们只要枚举所有的a、b、c
- 能够让上面的等式成立即可
- 如何枚举所有所有的a、b、c呢?
- 通过之前的递归实现排列型枚举、也是全排列即可
C/C++
#include JAVA
import java.util.*;
public class Main{
static int N = 10;
static int[] path = new int[N]; // 用于储存全排列
static boolean[] st = new boolean[N];
static Scanner in = new Scanner(System.in);
static int n,ans = 0;
public static void main(String[] args){
n = in.nextInt();
dfs(1);
System.out.println(ans);
}
private static void dfs(int u){
// 此时path以及存好了全排列
if(u == N){
for(int i = 1;i <= 7;i++){
for(int j = i+1;j <= 8;j++){
int a = cala(1,i);
int b = cala(i+1,j);
int c = cala(j+1,9);
if(n*c == a*c + b) ans++;
}
}
}
for(int i = 1;i < N ;i++){
if(!st[i]){
path[u] = i;
st[i] = true;
dfs(u+1);
st[i] = false;
}
}
}
public static int cala(int l,int r){
int sum = 0;
for(int i = l;i <= r;i++){
sum *= 10;
sum += path[i];
}
return sum;
}
}
思路二:
- 根据上面可知 n * c = a * c + b
- 等式中三个位置数,知道其中两个即可
- 那么我们枚举a和c,就可以得到b
- 判断b是否符合要求、如果符合要求即可
c/c++
#include Java
import java.util.*;
public class Main{
static int N = 10;
static boolean[] st = new boolean[N]; // 每一位只能使用一次
static Scanner in = new Scanner(System.in);
static int n,ans = 0;
public static void main(String[] args){
n = in.nextInt();
// 从1开始搜索,此时a为0
dfs_a(1,0);
System.out.println(ans);
}
private static void dfs_a(int u,int a){
// 第十位
if(u == N) return;
// 剪枝,a不可能大于n
if(a > n) return;
// 递归遍历c
if(a > 0) dfs_c(u,a,0);
for(int i = 1;i < N;i++){
if(!st[i]){
st[i] = true;
// 递归a
dfs_a(u+1,a*10+i);
st[i] = false;
}
}
}
private static void dfs_c(int u,int a,int c){
if(u == N) return;
// 判断此时的ac是否满足条件
if(check(a,c)) ans++;
for(int i = 1;i < N;i++){
if(!st[i]){
st[i] = true;
// 递归c
dfs_c(u+1,a,c*10+i);
st[i] = false;
}
}
}
// 判断是否满足条件
private static boolean check(int a,int c){
int b = n * c - a * c;
// a b c 都是正数
if(b <= 0 || a <= 0 || c <= 0) return false;
// 判断是否有重复使用的数
boolean[] backup = new boolean[N];
// 使用备份来判断
for(int i = 1;i < N;i++) backup[i] = st[i];
while(b > 0){
int x = b %10;
b /= 10;
if(x == 0 || backup[x]) return false;
backup[x] = true;
}
// 判断1~9是否每一位都使用过
for(int i = 1;i < N;i++){
if(!backup[i]) return false;
}
return true;
}
}