46.整理华子面经+笔试+排序算法
算法题
对于一个给定的数字N,找出从1到N中能被N整除的数?
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()){
int i = scanner.nextInt();
Set solve = solve(i);
for (Integer integer : solve) {
System.out.println(integer);
}
}
}
public static Set solve(int n){
Set res=new HashSet<>();
for (int i = 1; i <=Math.pow(n,0.5) ; i++) {
//同时找到能整除的i和n/i
if(n%i==0){
res.add(i);
res.add(n/i);
}
}
return res;
} 数组中的最长山脉
public int longestMountain(int[] arr) {
int n = arr.length;
int ans = 0;
int left = 0;
while (left + 2 < n) {
int right = left + 1;
if (arr[left] < arr[left + 1]) {
while (right + 1 < n && arr[right] < arr[right + 1]) {
++right;
}
if (right < n - 1 && arr[right] > arr[right + 1]) {
while (right + 1 < n && arr[right] > arr[right + 1]) {
++right;
}
ans = Math.max(ans, right - left + 1);
}
}
left = right;
}
return ans;
}面试题
满二叉树?完全二叉树?二叉查找树?红黑树?
- 满二叉树:一个二叉树,每个层的节点数都达到了最大值,它的节点总数是2的n次方-1,其中n为层数
- 完全二叉树:如果一个二叉树的深度为h,除了第h层之外,其余各层的节点数都达到了最大的个数,且h层的所有节点都聚集在左边
- 二叉查找树:每个节点的左子树都比当前节点值小,每个节点的右子树都比当前节点数大
- 红黑树:自平衡的二叉搜索树
wait和sleep的区别?
sleep是Thread的静态方法,在调用之后,让调用线程进入睡眠状态,让出执行机会给其他的线程,等到休眠时间结束以后,线程进入就绪状态和其他线程一起竞争cpu,整个过程不释放锁,到达指定时间后被唤醒
wait是Object的方法,对象调用wait后,进入锁对象的等待池,同时释放当前锁,使得其他线程能够访问,需要搭配notify来唤醒
死锁?
互斥,请求与等待,不可剥夺,环路等待
死锁的预防:
- 一次性分配所有资源->破坏请求条件
- 只要有一个资源得不到分配,也不给这个进程分配其他资源->破坏保持条件
- 当某个进程获得了资源,但得不到其他资源,释放已占有资源->破坏不可剥夺条件
- 资源有序分配->给每类资源赋予一个编号,每个进程按照编号递增的顺序请求资源,释放则相反->破坏环路等待
死锁的检测:
通过检测有向图是否存在环来检测,从一个节点触发进行dfs,对访问过的节点进行标记,如果访问到了已经标记的节点,说明有死锁情况的发生
可以通过jps -l列出java进程号,再通过jstack 进程号定位具体的信息
解除死锁的方式:
- 撤销进程法:撤销限于死锁的所有进程或者逐个撤销死锁的进程直到死锁不存在
- 资源剥夺法:从限于死锁的进程中逐个强迫放弃占用的资源,直到死锁消失,从另外的进程那里强行剥夺足够数量的资源分配给死锁进程,解除死锁的状态
- 鸵鸟算法:不管
ThreadLocal详解
ThreadLocal主要做的是数据隔离,数据只属于当前线程,变量的数据对于别的线程而言是隔离的,多线程环境下可以防止自己的变量被其他线程篡改
应用场景:
Spring的事务主要是通过AOP和ThreadLocal来保证的,ThreadLocal保存的是每个线程自己的连接
可以作为一个当前线程全局的变量来使用,一个线程经常要通过若干方法调用,而一些信息基本是一致的比如用户身份信息
底层原理:
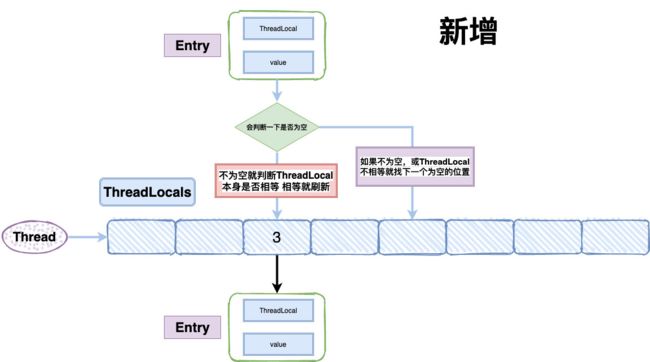
其底层是一个叫ThreadLocalMap的k-v键值对,在Thread类中,可以看到有这样的变量,每个Thread都维护了自己的ThreadLocals变量,当线程创建ThreadLocal的时候,数据实际上存储在Thread的这个变量里,从而实现了线程之间的隔离
public class Thread implements Runnable {
……
/* ThreadLocal values pertaining to this thread. This map is maintained
* by the ThreadLocal class. */
ThreadLocal.ThreadLocalMap threadLocals = null;
/*
* InheritableThreadLocal values pertaining to this thread. This map is
* maintained by the InheritableThreadLocal class.
*/
ThreadLocal.ThreadLocalMap inheritableThreadLocals = null;
……
对于ThreadLocalMap,其底部维护了一个Entry数组,Entry被设计为弱引用,由于数组的存在,一个线程可以使用多个ThreadLocal来存放不同类型的对象,这些对象都放在Thread的ThreadLocalMap的数组里
static class ThreadLocalMap {
private static final int INITIAL_CAPACITY = 16;
private ThreadLocal.ThreadLocalMap.Entry[] table;
static class Entry extends WeakReference> {
/** The value associated with this ThreadLocal. */
Object value;
Entry(ThreadLocal k, Object v) {
super(k);
value = v;
}
}
……
} 它解决hash冲突的方式是在插入过程中,如果遇到空的位置,就初始化一个Enrty放在对象位置上,否则如果遇到此位置有值且key相等,进行替换,如果key不相等,就寻找下一个位置,直到空位置为止,get的时候方法也与之类似
这个ThreadLocal的对象是存放在哪的?
在Java中,栈的内存属于单个线程,是线程私有的,堆内存是对所有线程可见的,ThreadLocal实际上也是被创建在堆上的,只是通过一些技巧将可见性修改成了线程可见,也因此,如果想使用父子线程共享的ThreadLocal可以使用InheritableThreadLocal这个变量,传递的逻辑其实就是在初始化的时候,把父线程的ThreadLocal的该变量赋值到子线程
ThreadLocal的问题:
内存泄漏问题,不管当前内存是否足够,弱引用都会被垃圾回收,当ThreadLocal没有外部引用的时候,发生GC回收,如果ThreadLocal的线程一直持续运行(比如线程池),那么这个Entry中的value就可能一直得不到回收,形成null-value的entry,如果不设计成弱引用,会造成整个entry都回收不掉
解决方法就是显示的调用remove方法
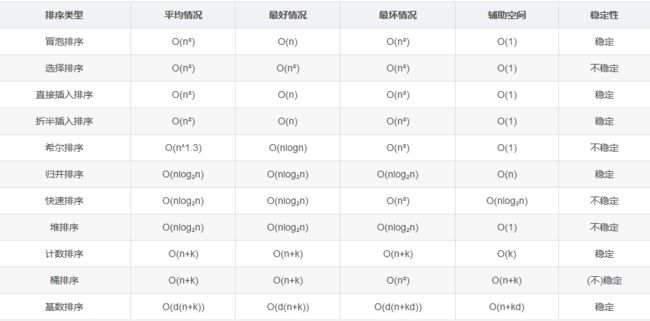
排序算法?
快速排序算法和归并算法的区别?
他们都是分而治之的算法思想的实现
归并排序无差别的将数组一分为2,然后不停的合并两个有序的数组
快速排序在分这件事上做文章但是没有合并的过程
术语说明:
-
稳定和不稳定:如果两个数相等,a本来在b之前,排序之后a到了b的后面,说明不稳定
-
k:桶的个数,n数据规模
算法的分类:
- 快速排序,归并排序,堆排序和冒泡排序都属于比较排序,每个数都需要通过与其他数比较,才能确定自己的位置
- 计数排序,基数排序,桶排序属于非比较排序,其时间复杂度比较低,单一般需要占用空间来确定位置,对数据的规模要求
冒泡排序:它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换
public static int[] bubbleSort(int[] array) {
if (array.length == 0)
return array;
for (int i = 0; i < array.length; i++) {
boolean isSorted = false;
for (int j = 0; j < array.length - 1 - i; j++) {
if (array[j + 1] < array[j]) {
isSorted = true;
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
}
}
if(!isSorted)break;
}
return array;
}选择排序:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾
public static int[] selectionSort(int[] array) {
if (array.length == 0)
return array;
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i; j < array.length; j++) {
if (array[j] < array[minIndex]) //找到最小的数
minIndex = j; //将最小数的索引保存
}
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
return array;
}插入排序:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
public static int[] insertionSort(int[] array) {
if(array.length==0)return array;
int current;
for (int i = 0; i < array.length-1; i++) {
current=array[i+1];
int preIndex=i;
while (preIndex>=0&¤t希尔排序:特殊的插入排序,对数据按照增量进行了分组处理,当增量减少到1的时候,整个array正好被分成了一组,也就是完成了排序
public static int[] ShellSort(int[] array) {
int len = array.length;
int temp, gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
return array;
}归并排序:使用分治的思想,先使得每个子序列有序,再使得整体有序
public void merge(int[] nums, int left, int right) {
int mid = left + ((right - left) >> 1);
if (left < right) {
merge(nums, left, mid);
merge(nums, mid + 1, right);
mergeSort(nums, left, mid, right);
}
}
public void mergeSort(int[] nums, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int index = 0;
int index1 = left, index2 = mid + 1;
while (index1 <= mid && index2 <= right) {
if (nums[index1] <= nums[index2]) {
temp[index++] = nums[index1++];
} else {
temp[index++] = nums[index2++];
}
}
//把左边剩余的数移入数组
while (index1 <= mid) {
temp[index++] = nums[index1++];
}
//把右边剩余的数移入数组
while (index2 <= right) {
temp[index++] = nums[index2++];
}
//把新数组中的数覆盖nums数组
System.arraycopy(temp, 0, nums, left, right - left + 1);
}快速排序:选择一个基准,遍历数组,将比基准小的放在左边,大的放右边,结束后,基准位于中间的位置
//写法一
private static void quickSort(int[] arr){
if(arr==null||arr.length==0)return;
int begin=0;
int end=arr.length-1;
quickSortHelper(arr,begin,end);
}
private static void quickSortHelper(int[] arr, int begin, int end) {
if(end<=begin)return;//递归终止条件
int i=begin;
int j=end;
int index=arr[begin];//这样的写法index不能是随机数,只能是第一个
while (i=index){
j--;
}
arr[i]=arr[j];
//再移动i
while (i=right)return;
int p=partition(arr,left,right);
//对划分区域后的子区域进行继续划分
sortHelper(arr,left,p-1);
sortHelper(arr,p+1,right);
}
//返回划分区域后的中间指针
private int partition(int[] arr, int left, int right) {
//随机操作(+1操作)[0,right-left-1]->(+left操作)[0,right-left]->[left,right];
int index = random.nextInt(right - left + 1) +left;
swap(arr,index,left);
int cur=left+1;//此指针用于遍历
int lastOfFirst=left;//此指针指向两个区域分割的位置
int pivot=arr[left];//每次以第一个元素为分界
//[left+1,part]的元素小于pivot,一开始定义为空区间
//(part,cur)的元素大于pivot,以开水定义为空区间
while (cur 堆排序:每个节点的值都大于其左孩子和右孩子节点的值,称之为大根堆,否则称之为小根堆,并且堆是一个完全二叉树,如果映射成数组,父节点索引表示为(i-1)/2,左孩子索引为2*i+1,右孩子索引为2*i+2
//堆排序
public static void heapSort(int[] arr) {
//构造大根堆
heapInsert(arr);
int size = arr.length;
while (size > 1) {
//固定最大值
swap(arr, 0, size - 1);
size--;
//构造大根堆
heapify(arr, 0, size);
}
}
//构造大根堆(通过新插入的数上升)
public static void heapInsert(int[] arr) {
for (int i = 0; i < arr.length; i++) {
//当前插入的索引
int currentIndex = i;
//父结点索引
int fatherIndex = (currentIndex - 1) / 2;
//如果当前插入的值大于其父结点的值,则交换值,并且将索引指向父结点
//然后继续和上面的父结点值比较,直到不大于父结点,则退出循环
while (arr[currentIndex] > arr[fatherIndex]) {
//交换当前结点与父结点的值
swap(arr, currentIndex, fatherIndex);
//将当前索引指向父索引
currentIndex = fatherIndex;
//重新计算当前索引的父索引
fatherIndex = (currentIndex - 1) / 2;
}
}
}
//将剩余的数构造成大根堆(通过顶端的数下降)
public static void heapify(int[] arr, int index, int size) {
int left = 2 * index + 1;
int right = 2 * index + 2;
while (left < size) {
int largestIndex;
//判断孩子中较大的值的索引(要确保右孩子在size范围之内)
if (arr[left] < arr[right] && right < size) {
largestIndex = right;
} else {
largestIndex = left;
}
//比较父结点的值与孩子中较大的值,并确定最大值的索引
if (arr[index] > arr[largestIndex]) {
largestIndex = index;
}
//如果父结点索引是最大值的索引,那已经是大根堆了,则退出循环
if (index == largestIndex) {
break;
}
//父结点不是最大值,与孩子中较大的值交换
swap(arr, largestIndex, index);
//将索引指向孩子中较大的值的索引
index = largestIndex;
//重新计算交换之后的孩子的索引
left = 2 * index + 1;
right = 2 * index + 2;
}
}
//交换数组中两个元素的值
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}计数排序:将输入的数据转化为键存储在额外开辟的数组空间中,计数排序要求输入的数据必须是有确定范围的整数,当输入元素时n个0到k之间的整数时,运行时间为O(n+k)
public static int[] CountingSort(int[] array) {
if (array.length == 0) return array;
int bias, min = array[0], max = array[0];
//统计最大最小数
for (int i = 1; i < array.length; i++) {
if (array[i] > max)
max = array[i];
if (array[i] < min)
min = array[i];
}
bias = - min;//为了能让桶的零索引对应最小值
int[] bucket = new int[max - min + 1];//新建桶
Arrays.fill(bucket, 0);
for (int i = 0; i < array.length; i++) {
bucket[array[i] + bias]++;
}
int index = 0, i = 0;
//排序数组
while (index < array.length) {
if (bucket[i] != 0) {
array[index] = i - bias;
bucket[i]--;
index++;
} else
i++;
}
return array;
}桶排序:计数排序的升级版本,利用了函数的映射关系,高效与否在于映射函数的确定,将数据分布到有限数量的桶中,每个桶再分别排序
public static ArrayList BucketSort(ArrayList array, int bucketSize) {
if (array == null || array.size() < 2)
return array;
int max = array.get(0), min = array.get(0);
// 找到最大值最小值
for (int i = 0; i < array.size(); i++) {
if (array.get(i) > max)
max = array.get(i);
if (array.get(i) < min)
min = array.get(i);
}
int bucketCount = (max - min) / bucketSize + 1;//计算桶的数量
ArrayList> bucketArr = new ArrayList<>(bucketCount);
ArrayList resultArr = new ArrayList<>();//最后要返回的数组
//初始化
for (int i = 0; i < bucketCount; i++) {
bucketArr.add(new ArrayList());
}
//向每个桶中添加元素
for (int i = 0; i < array.size(); i++) {
bucketArr.get((array.get(i) - min) / bucketSize).add(array.get(i));
}
//对每个桶的数据进行排序操作
for (int i = 0; i < bucketCount; i++) {
if (bucketSize == 1) { //在bucketsize为1的时候,递归的终止条件
resultArr.addAll(bucketArr.get(i));
} else {
if (bucketCount == 1)
bucketSize--;
//递归的采用桶排序
ArrayList temp = BucketSort(bucketArr.get(i), bucketSize);
resultArr.addAll(temp);
}
}
return resultArr;
} 基数排序:对数字的每一位开始排序,从最低的个位开始,推到高位
/**
* 基数排序
* @param array
* @return
*/
public static int[] RadixSort(int[] array) {
if (array == null || array.length < 2)
return array;
// 1.先算出最大数的位数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
max = Math.max(max, array[i]);
}
int maxDigit = 0;
while (max != 0) {
max /= 10;
maxDigit++;
}
int mod = 10, div = 1;
ArrayList> bucketList = new ArrayList>();
for (int i = 0; i < 10; i++)
bucketList.add(new ArrayList());
for (int i = 0; i < maxDigit; i++, mod *= 10, div *= 10) {
for (int j = 0; j < array.length; j++) {
int num = (array[j] % mod) / div;
bucketList.get(num).add(array[j]);
}
int index = 0;
for (int j = 0; j < bucketList.size(); j++) {
for (int k = 0; k < bucketList.get(j).size(); k++)
array[index++] = bucketList.get(j).get(k);
bucketList.get(j).clear();
}
}
return array;
}