训练二元分类器及三种评估方法

分类器

MINIST

使用MNIST数据集，这是一组由美国高中生和人口调查局员工手写的70000个数字的图片

Scikit-Learn提供了许多助手功能来帮助你下载流行的数据集。MNIST也是其中之一。下面是获取MNIST数据集的代码

from sklearn.datasets import fetch_openml
minst = fetch_openml('mnist_784',version=1)
minst.keys()

dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])

Scikit-Learn加载的数据集通常具有类似的字典结构，包括：

• DESCR键，描述数据集。
• data键，包含一个数组，每个实例为一行，每个特征为一列。
• target键，包含一个带有标记的数组。

X,y = minst["data"],minst["target"]
print(X.shape,y.shape)

(70000, 784) (70000,)

看数据情况，共有7万张图片，每张图片有784个特征。
图片是28×28像素，每个特征代表了一个像素点的强度，从0（白色）到255（黑色）。
随手抓取一个实例的特征向量X[0]，将其重新形成一个28×28数组，然后使用Matplotlib的imshow（）函数将其显示出来。图形显示与y[0]一样

import matplotlib as mpl
import matplotlib.pyplot as plt

some_digit = X[0]
some_digit_image = some_digit.reshape(28,28)

plt.imshow(some_digit_image,cmap='binary')#plt.imshow()函数负责对图像进行处理，并显示其格式，但是不能显示。其后跟着plt.show（）才能显示出来。
plt.title('%s'%y[0]) # y[0]为字符串
plt.axis('off')
plt.show()

创建测试集和训练集。但MNIST数据集已经分成训练集（前6万张图片）和测试集（最后1万张图片）了

import numpy as np
y = y.astype(np.uint8)

X_train,X_test,y_train,y_test = X[:60000],X[60000:],y[:60000],y[60000:]

先将训练集数据混洗（就是打乱实例的排列顺序），这样能保证交叉验证时所有的折叠都差不多

训练二元分类器

先尝试识别一个数字，比如5,则为“数字5检测器”,其分类结果为5和非5。为此分类任务创建目标向量

y_train_5 = (y_train == 5) # 为5的都为真，其他都为假
y_test_5 = (y_test == 5)

先创建一个分类器并在整个训练集上进行训练，选择随机梯度下降（SGD）分类器，使用Scikit-Learn的SGDClassifier类即可。

from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42) #SGDClassifier在训练时是完全随机的，为得到可复现的结果，需要设置参数random_state
sgd_clf.fit(X_train,y_train_5)

用分类器监测数字5的图片，查看分类结果

sgd_clf.predict([some_digit]) # 返回True,表示分类器猜这个数字为5，y[0]就是5，预测准确

评估分类器

使用交叉验证测量准确率

Scikit-Learn提供cross_val_score（）这一类交叉验证的函数，我是跟着书本码的笔记，书本写了一个自行实现交叉验证的代码如下:
每个折叠由StratifiedKFold执行分层抽样产生，其所包含的各个类的比例符合整体比例。每个迭代会创建一个分类器的副本，用训练集对这个副本进行训练，然后用测试集进行预测。最后计算正确预测的次数，输出正确预测的比率。

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

skfolds = StratifiedKFold(n_splits=3,random_state=42,shuffle=True) #StratifiedKFold 将训练集做有放回分层抽样，分为新的训练集和验证集，随机分三次，取出索引

for train_index,test_index in skfolds.split(X_train,y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = y_train_5[train_index]
    
    X_test_fold = X_train[test_index]
    y_test_fold = y_train_5[test_index]
    
    clone_clf.fit(X_train_folds,y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct/len(y_pred))  # 0.9669,0.91625,0.96785

用cross_val_score（）函数来评估SGDClassifier模型，采用K-折交叉验证法（3个折叠）。记住，K-折交叉验证的意思是将训练集分解成K个折叠（在本例中，为3折），然后每次留其中1个折叠进行预测，剩余的折叠用来训练

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf,X_train,y_train_5,cv=3,scoring='accuracy')

array([0.95035, 0.96035, 0.9604 ])

所有折叠交叉验证的准确率（正确预测的比率）超过93%？看起来挺神奇的，是吗？不过在你开始激动之前，我们来看一个蠢笨的分类器，它将每张图都分类成“非5”

from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
    def fit(self,X,y=None):
        return self
    def predict(self,X):
        return np.zeros((len(X),1),dtype=bool)
    
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf,X_train,y_train_5,cv=3,scoring='accuracy') # array([0.91125, 0.90855, 0.90915])

sum(np.where(y_train_5,1,0))/60000 #0.09035,只有大约10%的数字为5，训练集为有偏数据集

准确率超过90%！这是因为只有大约10%的图片是数字5，所以如果你猜一张图不是5，90%的概率你都是正确的，这说明准确率通常无法成为分类器的首要性能指标，特别是当你处理有偏数据集时（即某些类比其他类更为频繁）

混淆矩阵

评估分类器性能的更好方法是混淆矩阵，其总体思路就是统计A类别实例被分成为B类别的次数

要计算混淆矩阵，需要先有一组预测才能将其与实际目标进行比较。当然，可以通过测试集来进行预测，但是现在先不要动它（测试集最好留到项目的最后，准备启动分类器时再使用）。作为替代，可以使用cross_val_predict（）函数.与cross_val_score（）函数一样，cross_val_predict（）函数同样执行K-折交叉验证，但返回的不是评估分数，而是每个折叠的预测

计算混淆矩阵

from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf,X_train,y_train_5,cv=3)

现在使用confusion_matrix（）函数来获取混淆矩阵了。只需要给出目标类别（y_train_5）和预测类别（y_train_pred）即可

from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5,y_train_pred)

array([[53892,   687],
       [ 1891,  3530]], dtype=int64)

混淆矩阵中的行表示实际类别，列表示预测类别。本例中第一行表示所有“非5”（负类）的图片中：53892张被正确地分为“非5”类别（真负类），687张被错误地分类成了“5”（假正类）；第二行表示所有“5”（正类）的图片中：1891张被错误地分为“非5”类别（假负类），3530张被正确地分在了“5”这一类别（真正类）

计算精度和灵敏度

计算模型的精确度和灵敏度（召回率）
精确度指模型被正确地预测为正的数量占被模型预测为正的数量的比例
灵敏度，也称召回率。指模型被正确地预测为正的数量占实际为正的数量的比例

from sklearn.metrics import precision_score,recall_score
print("精确度:",precision_score(y_train_5,y_train_pred)) # 3530/（3530+687）,表示当sgd_clf分类器说一个数值是5时，只有84%的概览是正确的
print("灵敏度:",recall_score(y_train_5,y_train_pred)) # 3530/(3530+1891),表示当sgd_clf分类器只能识别出65%的数字5

模型进行分类预测的过程会倾向于把样本分类到我们所感兴趣的目标，也就是若灵敏度很高，但精确度很低，这样虽然能够把非5找出来，但是非5也会被包含在其中。
因此，在这两个指标上延伸出一个新的变量，叫F1_Score，它是精确度和灵敏度的调和平均数

from sklearn.metrics import f1_score
print("调和平均数:",f1_score(y_train_5,y_train_pred))#调和平均数: 0.7325171197343846

F1分数对那些具有相近的精度和召回率的分类器更为有利。这不一定能一直符合你的期望：在某些情况下，你更关心的是精度，而另一些情况下，你可能真正关心的是召回率。例如，假设你训练一个分类器来检测儿童可以放心观看的视频，那么你可能更青睐那种拦截了很多好视频（低召回率），但是保留下来的视频都是安全（高精度）的分类器，而不是召回率虽高，但是在产品中可能会出现一些非常糟糕的视频的分类器（这种情况下，你甚至可能会添加一个人工流水线来检查分类器选出来的视频）。反过来说，如果你训练一个分类器通过图像监控来检测小偷：你大概可以接受精度只有30%，但召回率能达到99%（当然，安保人员会收到一些错误的警报，但是几乎所有的窃贼都在劫难逃）。

精度/召回率权衡

要理解这个权衡过程，我们来看看SGDClassifier如何进行分类决策。对于每个实例，它会基于决策函数计算出一个分值，如果该值大于阈值，则将该实例判为正类，否则便将其判为负类。图3-3显示了从左边最低分到右边最高分的几个数字。假设决策阈值位于中间箭头位置（两个5之间）：在阈值的右侧可以找到4个真正类（真的5）和一个假正类（实际上是6）。因此，在该阈值下，精度为80%（4/5）。但是在6个真正的5中，分类器仅检测到了4个，所以召回率为67%（4/6）。现在，如果提高阈值（将其挪动到右边箭头的位置），假正类（数字6）变成了真负类，因此精度得到提升（本例中提升到100%），但是一个真正类变成一个假负类，召回率降低至50%。反之，降低阈值则会在增加召回率的同时降低精度。

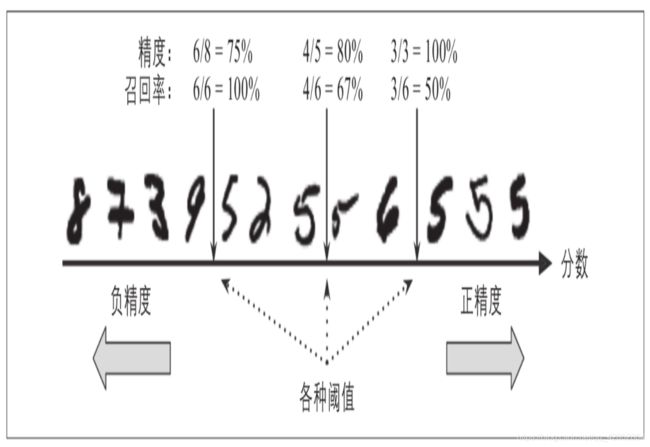
Scikit-Learn不允许直接设置阈值，但是可以访问它用于预测的决策分数。不是调用分类器的predict（）方法，而是调用decision_function（）方法，这种方法返回每个实例的分数，然后就可以根据这些分数，使用任意阈值进行预测了

y_scores = sgd_clf.decision_function([some_digit])
y_scores  # array([2164.22030239])

# 提高阈值可以降低召回率。当阈值小于y_scores时，分类器可以检测到该图，当阈值高于y_scores时，就错过了这张图。
threshold = 3000
y_some_digit_pred = (y_scores > threshold)
print(y_some_digit_pred) # [False]

如何决定使用什么阈值呢？首先，使用cross_val_predict（）函数获取训练集中所有实例的分数，但是这次需要它返回的是决策分数而不是预测结果：

y_scores = cross_val_predict(sgd_clf,X_train,y_train_5,cv=3,method="decision_function")

通过y_scores这些分数，使用precision_recall_curve()函数来计算所有可能的阈值的精度和召回率

from sklearn.metrics import precision_recall_curve
precisions,recalls,thresholds = precision_recall_curve(y_train_5,y_scores)

最后，使用Matplotlib绘制精度和召回率相对于阈值的函数图。从图中根据需要选择合适的阈值

import matplotlib.pyplot as plt

def plot_precision_recall_vs_threshold(precisions,recalls,thresholds):
    plt.plot(thresholds,precisions[:-1],'b--',label='Precision')
    plt.plot(thresholds,recalls[:-1],'g-',label='Recall')

plot_precision_recall_vs_threshold(precisions,recalls,thresholds)
plt.legend()
plt.grid()
plt.show()

# 假设要求精度达到90%，则最小阈值为:
threshold_90_precision = thresholds[np.argmax(precisions>=0.9)]
print(threshold_90_precision) #3370.0194991439594

# 要求90%的精确度下计算现在的召回率
y_train_pred_90 = (y_scores >= threshold_90_precision)
print("精确度:",precision_score(y_train_5,y_train_pred_90)) #精确度: 0.9000345901072293
print("灵敏度:",recall_score(y_train_5,y_train_pred_90)) # 灵敏度: 0.4799852425751706

ROC曲线

还有一种经常与二元分类器一起使用的工具，叫作受试者工作特征曲线（简称ROC）。ROC曲线绘制的是灵敏度TPR（召回率）和FPR（1-特异度）的关系。特异度指模型被正确地预测为负的数量占被模型预测为负的数量的比例。
要绘制ROC曲线，首先需要使用roc_curve（）函数计算多种阈值的召回率和1-特异度：

from sklearn.metrics import roc_curve
fpr,tpr,thresholds = roc_curve(y_train_5,y_scores)

def plot_roc_curve(fpr,tpr,label=None):
    # 绘制了所有可能阈值的假正率与真正率的关系
    plt.plot(fpr,tpr,linewidth=2,label=label)
    plt.plot([0,1],[0,1],'k--')
    plt.grid()
    
plot_roc_curve(fpr,tpr)
plt.show()

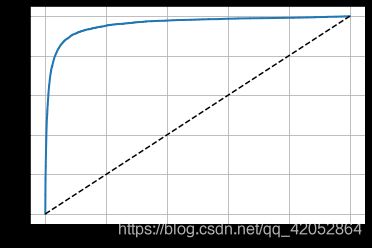
召回率（TPR）越高，分类器产生的假正类率（FPR）就越高。虚线表示纯随机分类器的ROC曲线、一个优秀的分类器应该离这条线越远越好（向左上角）。
有一种比较分类器的方法是测量曲线下面积（AUC）。完美的分类器的ROC AUC等于1，而纯随机分类器的ROC AUC等于0.5。Scikit-Learn提供计算ROC AUC的函数：

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5,y_scores) # 0.9604938554008616