RetinaNet：Focal Loss for Dense Object Detection

RetinaNet：Focal Loss for Dense Object Detection

一阶段目标检测算法在训练时面临类别不平衡的问题。对一张图片，仅仅只包含几个物体，但是检测器通常会有 $10^4-10^5$个候选框。类别不平衡导致训练效率很低，因为easy negative样本会给训练提供无用的学习信号。而且类别不平衡也容易退化模型。通常的解决方法是使用hard negative mining 在训练期间挖掘困难样本。

hard negative ，困难样本，指在对负样本分类时，loss比较大的那些样本或者容易将负样本看成正样本的那些样本。 hard negative mining就是多找一些困难样本加入负样本集，进行训练，这样会比easy negative组成的负样本集效果更好。

Focal Loss

Focal loss的设计是为了解决一阶段目标检测算法前景和背景类别不平衡的问题。

对于二分类问题，假设$y\in \left\{\pm 1\right\}$表示gt类别标签，$p\in \left[0,1\right]$表示当$y=1$时模型预测的类别概率值，那么 交叉熵函数（cross entropy）定义如下：
$$CE\left(p,y\right)=\{\begin{array}{cc}-log\left(p\right)& ify=1\\ -log\left(1-p\right)& otherwise\end{array}$$

假设定义$p_t$如下，那么CE函数重写为$CE\left(p,y\right)=CE\left(p_t\right)=-log\left(p_t\right)$
$$p_t=\{\begin{array}{cc}p& ify=1\\ 1-p& otherwise\end{array}$$

通常情况下，解决类别不平衡的方法是通过对类别$1$引入权重因子$\alpha \in \left[0,1\right]$，对类别$-1$引入$1-\alpha$。那么CE函数的一个简单扩展可定义为$CE\left(p_t\right)=-{\alpha }_{t}log\left(p_t\right)$。

简单分类的负例是loss的最大组成，并且主导着梯度。当参数$\alpha$平衡正例/负例的重要性时，它并不能区分easy样本和hard样本。论文中重塑了loss函数，降低easy样本的权重，并且在训练时关注hard negatives.

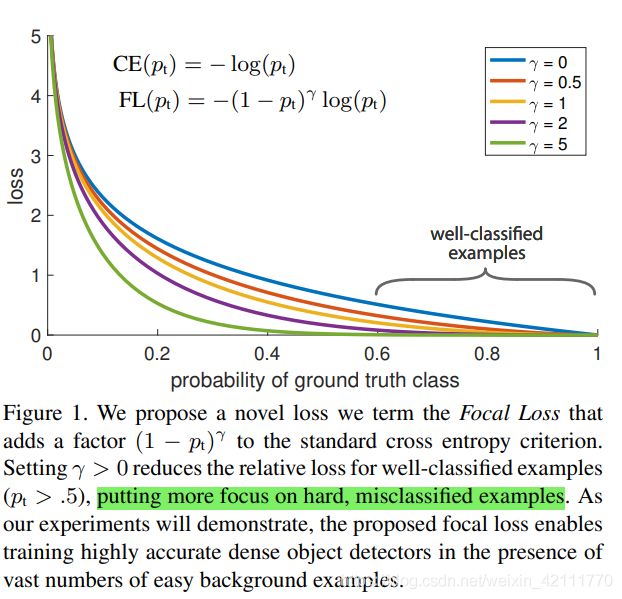
在CE loss 前添加一个调制因子${\left(1-p_t\right)}^{\gamma }$，其中可调参数$\gamma \ge 0$。focal loss定义如下：

$$FL\left(p_t\right)=-{\left(1-p_t\right)}^{\gamma }log\left(p_t\right)$$

下图可视化了focal loss在可调参数取值$\gamma \in \left[0,5\right]$时的函数曲线。当一个样本被误分且$p_t$取值较小时，调制参数${\left(1-p_t\right)}^{\gamma }$接近于1，loss不受影响。随着$p_t$越接近于1，${\left(1-p_t\right)}^{\gamma }$接近于0，对于分类正确的样本，loss值的权重被降低。参数$\gamma$平滑地调整easy样本的加权速率。当参数$\gamma =0$，FL等价于CE，随着$\gamma$的增加，调制参数的影响也随之增加。在论文中的实验，它们发现当$\gamma =2$时，表现最好。

调制因子减少easy样本的loss贡献并且扩展样本接收低loss的范围。例如，设定$\gamma =2$，当一个样本被正确分类，且它的概率取值$P_t=0.9$时，$CE\left(p_t=0.9\right)=-log\left(0.9\right)$，$FL\left(p_t=0.9\right)=-{\left(1-0.9\right)}^{2}log\left(0.9\right)=1/100CE\left(p_t=0.9\right)$，调制因子的存在使得此样本的FL值是CE函数值的$1/100$倍。当$P_t\approx 0.968$时，将会有1000倍的差异。当$p_t\le 0.5时$，样本被错误分类时，$FL\left(p_t\le 0.5\right)\le -{\left(1-0.5\right)}^{2}log\left(p_t\right)=\frac{1}{4}CE\left(p_t\le 0.5\right)$，loss最多下降四倍，这增加了纠正错误分类样本的重要性。

添加$\alpha$参数平衡focal loss，实验验证带有$\alpha$参数的focal loss能够比没有参数$\alpha$的focal loss提高模型性能。
$$FL\left(p_t\right)=-{\alpha }_t{\left(1-p_t\right)}^{\gamma }log\left(p_t\right)$$

Focal loss*

focal loss* 是另一种focal loss的实例演示。首先，定义变量$x_t$为$x_t=yx$，然后设定$p_t=\sigma \left(x_t\right)$。当$x_t>0$时，$p_t>0.5$，样本被正确分类。下一步，以$x_t$的形式，定义focal loss的另一种形式。
$$\begin{array}{cc}{p}_t^{\ast }& =\sigma \left(\gamma x_t+\beta \right)\\ F{L}^{\ast }& =-log\left(p_t^{\ast }\right)/\gamma \end{array}$$

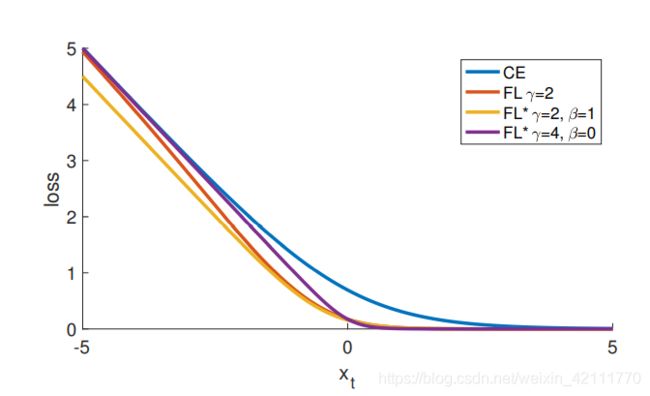
FL有两个参数，$\gamma$和$\beta$，控制loss曲线的坡度和偏倚。下图是FL选择不同参数和CE，FL的曲线图。从图中可以看出，FL和FL*减少分配给分类良好样本的loss值。

Derivatives

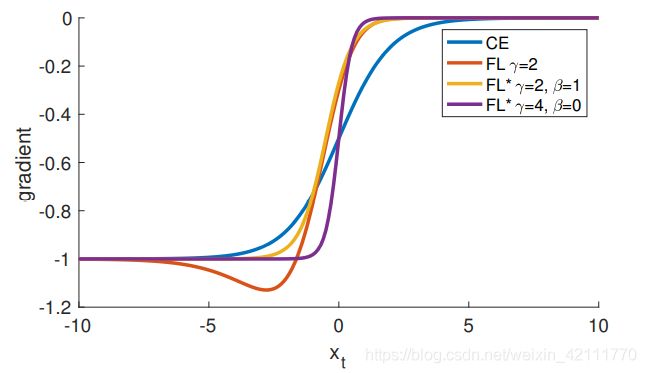
下面是CE，FL和FL的导数，下图是CE，FL和FL导数的图像展示。对所有的loss函数来说，对有高置信度的预测来说，导数值趋近于-1或者0。与CE不同的是，当$x_t>0$时，FL和FL*的导数值绝对值较小。
$$\begin{array}{c}\frac{dCE}{dx}=y\left(p_t-1\right)\\ \frac{dFL}{dx}=y{\left(1-p_t\right)}^{\gamma }\left(\gamma p_{t}log\left(p_t\right)+p_t-1\right)\\ \frac{dF{L}^{\ast }}{dx}=y\left(p_t^{\ast }-1\right)\end{array}$$

# This method is only for debugging
def py_sigmoid_focal_loss(pred,
                          target,
                          weight=None,
                          gamma=2.0,
                          alpha=0.25,
                          reduction='mean',
                          avg_factor=None):
    """PyTorch version of `Focal Loss `_.
    Args:
        pred (torch.Tensor): The prediction with shape (N, C), C is the
            number of classes
        target (torch.Tensor): The learning label of the prediction.
        weight (torch.Tensor, optional): Sample-wise loss weight.
        gamma (float, optional): The gamma for calculating the modulating
            factor. Defaults to 2.0.
        alpha (float, optional): A balanced form for Focal Loss.
            Defaults to 0.25.
        reduction (str, optional): The method used to reduce the loss into
            a scalar. Defaults to 'mean'.
        avg_factor (int, optional): Average factor that is used to average
            the loss. Defaults to None.
    """
    pred_sigmoid = pred.sigmoid()
    target = target.type_as(pred)
    pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)
    focal_weight = (alpha * target + (1 - alpha) *
                    (1 - target)) * pt.pow(gamma)
    loss = F.binary_cross_entropy_with_logits(
        pred, target, reduction='none') * focal_weight
    if weight is not None:
        if weight.shape != loss.shape:
            if weight.size(0) == loss.size(0):
                # For most cases, weight is of shape (num_priors, ),
                #  which means it does not have the second axis num_class
                weight = weight.view(-1, 1)
            else:
                # Sometimes, weight per anchor per class is also needed. e.g.
                #  in FSAF. But it may be flattened of shape
                #  (num_priors x num_class, ), while loss is still of shape
                #  (num_priors, num_class).
                assert weight.numel() == loss.numel()
                weight = weight.view(loss.size(0), -1)
        assert weight.ndim == loss.ndim
    loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
    return loss

Analysis of the Focal Loss

为了能够更好地理解focal loss，论文中分析了收敛loss模型的经验分布。默认backbone为ResNet101，$\gamma =2$，输入图像为600像素的模型。首先用模型预测大量的随机图片，然后挑选$10^7$个预测概率为负例的bbox和$10^5$和预测为正例的bbox。接下来，分开正例和负例，计算这些样本的FL值，然后normalize loss值以便总和为1。最后一句依据normalized loss从低到高进行排序，并分别为正例和负例画出它们在不同$\gamma$下的累计分布函数。

观察下图正例的累计分布函数，对于不同的$\gamma$值，它们的CDF很相近。然而负例的CDF 曲线受$\gamma$影响很大。当$\gamma =0$时，正例和负例的CDF是相似的。随着$\gamma$值增加，更多的关注集中在hard negative 样本上。当$\gamma =2$时，loss的绝大部分来自于一小部分样本。可以看出，FL能够有效地降低easy negative的影响，将更多的注意力放在hard negative 样本上。

累计分布函数（cumulative Distribution Function，CDF）是概率密度函数的积分，能完整描述一个实随机变量$X$的概率分布。$F_X\left(x\right)=P\left(X\le x\right)$

RetinaNet Detector

RetinaNet是一个简单的统一的网络，由backbone网络和两个特定任务子网络组成。backbone选用Resnet和FPN架构，构建$P_3$到$P_7$的特征图金字塔，其中$P_l$中的$l$表示$2^l$个像素低于输入图像。金字塔每层的特征都有256个通道。
$P_3$到$P_7$的特征是从相应的Resnet阶段计算得来（$C_3$到$C_5$）,$P_6$由$C_5$后接一个$3\times 3$卷积核，步长为$2$的卷积层得到，$P_6$同样后接一个同样的卷积，并计算ReLU函数得到$P_7$。$P_6$使用卷积步长代替下采样，$P_7$是为了提高大目标的检测。这些微调在保证准确率的同时提升速度。

Anchor

特征金字塔$P_3$到$P_7$，anchor的面积依次是$\left\{32^2，64^2，128^2，256^2，512^2\right\}$。anchor的aspect ratio为$\left\{1:2,1:1,2:1\right\}$，anchor的scale大小为$\left\{2^0,2^{1/3},2^{2/3}\right\}$，每一特征层共有$A=9$个anchors。

anchors依据IoU值进行正负例判定。当一个anchor的$IoU\ge 0.5$时，这个anchor则被设为gt目标框；当一个anchor的$0\le IoU<0.4$，这个anchor则被认为是背景框；当一个anchor的$0.4\le IoU<0.5$，在训练时，忽略这个anchor。

Classification Subnet

分类子网络是与FPN每一层特征图相连接的一个小的全卷积网络FCN，它预测特征图上每一个空间位置上$A$个anchor分别在$K$目标物体上的概率。分类子网络的参数对FPN不同层次特征图是共享的。以FPN上任意一个具有$C$通道的特定特征图为输入，经过$4$个卷积大小为$3\times 3$，通道为$C$，激活函数为ReLU的卷积层后，进入具有$KA$个filters的$3\times 3$卷积层。

Box Regression Subnet

回归子网络和分类子网络结构类似，只是输出方式有所不同。分类子网络和回归子网络平行存在，参数各异，不共享。

Experiments

初始化：对于backbone，ResNet-50/Resnet101需在数据集ImageNet1k上进行预训练。对于RetinaNet自网络上除了最后一层的所有新卷积层，初始偏置量为$b=0$，初始权重为$\sigma =0.01$的高斯。对于分类子网络中的最后一层卷积，初始偏置量$b=-log\left(\left(1-\pi \right)/\pi \right)$。

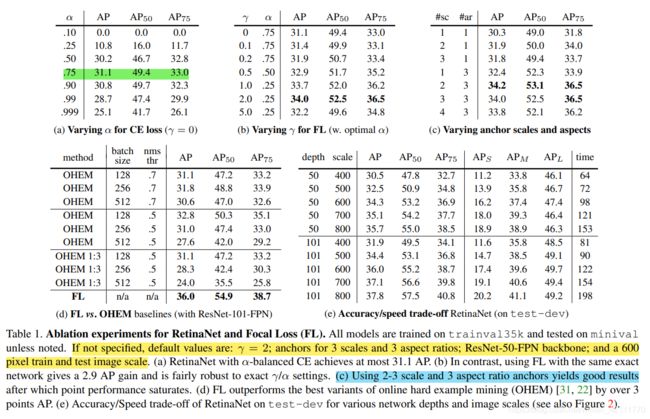
上图是对RetinaNet和focal loss的 ablation实验。如果没有特殊制定，默认$\gamma =2,\alpha =0.25$，anchor默认3个scale和3个aspect ratios。

inference阶段，为了提升速度，对于FPN每一层，设置检测置信度为0.05， 阈值选择后，至多选取前1k分数较高的预测框进行解码，然后合并FPN所有层的候选框，再进行NMS操作，NMS阈值为0.05，生成最后的检测结果。

参考

1. Focal Loss for Dense Object Detection