【论文笔记】FlowNet:有监督的光流估计(optical flow estimation)网络
本文是论文《FlowNet: Learning Optical Flow with Convolutional Networks》的阅读笔记。
一、概述
文章提出了一个名为FlowNet的网络,用有监督的方法根据输入的图像对来解决光流估计(optical flow estimation)问题。FlowNet有两种结构,一种是通用结构,另一种包括一个在不同图像位置的关联特征向量的层。又由于现有的数据集的数据量不足够训练CNN,所以又生成了一个合成的Flying Chairs数据集。
光流估计不仅需要每个像素精确的位置,还需要找到两张输入图之间的关联。这就要求不仅要学习到图像的特征表达,还需要学习到怎样将两张图像中不同的位置相匹配。
尽管可以用数据增强来扩充数据量,但是现有的光流数据集还是太小了,并且从视频素材中获取光流的ground truth是十分困难的。因此作者生成了一个合成的Flying Chairs数据集。FlowNet每秒大约可以处理10个图像对,达到了实时处理模型中的顶尖水平。下图是FlowNet的网络示意图,有点类似于UNet。
二、网络结构
FlowNet的输入是一个图像对,以及对应的光流ground truth。在FlowNet中信息先在收缩路径进行空间压缩,然后在扩张路径得到改善。文章在传统的CNN网络基础上加入了一个关联层(correlation layer)使网络具有匹配的能力,它用来学习和提取不同尺度的强特征,并找到它们之间的关联。
1. 收缩路径
收缩路径的设计有两种方案,一种是将所有输入图像在通道上堆叠(拼接),然后将它们输入到普通的网络中,这种方案被称作FlowNetSimple。另一种方案是将输入图像分别输入到两个独立但结构相同的处理流中,并在后面将两个流处理的结果进行合并。这种方式分别得到图像的特征,再将其合并。采用这种方案的网络被称为FlowNetCorr。
在FlowNetCorr中采用了关联层来促进网络的匹配过程。给定两个多通道的特征图 f 1 , f 2 f_1,f_2 f1,f2,其宽、高、通道数分别为 w , h , c w,h,c w,h,c。关联层用来比较每个 f 1 f_1 f1和 f 2 f_2 f2中的patch。第一个特征图中以位置 x 1 x_1 x1 为中心的patch和第二个特征图中以 x 2 x_2 x2 为中心的patch之间的关联性定义为:
c ( x 1 , x 2 ) = ∑ o ∈ [ − k , k ] × [ − k , k ] ⟨ f 1 ( x 1 + o ) , f 2 ( x 2 + o ) ⟩ c\left(\mathbf{x}_{1}, \mathbf{x}_{2}\right)=\sum_{\mathbf{o} \in[-k, k] \times[-k, k]}\left\langle\mathbf{f}_{1}\left(\mathbf{x}_{1}+\mathbf{o}\right), \mathbf{f}_{2}\left(\mathbf{x}_{2}+\mathbf{o}\right)\right\rangle c(x1,x2)=o∈[−k,k]×[−k,k]∑⟨f1(x1+o),f2(x2+o)⟩
每个patch是大小为 K : = 2 k + 1 K:=2k+1 K:=2k+1的正方形,上述公式和卷积操作类似,不同的是它没有参数。由于以上公式的计算量比较大,所以对最大位移做了限制,并且在两张特征图中引入了步长。给定最大位移 d d d,只需要对以位置 x 1 x_1 x1为中心,大小为 D : = 2 d + 1 D:=2d+1 D:=2d+1范围的邻居计算关联性 c ( x 1 , x 2 ) c(x_1,x_2) c(x1,x2)。使用步长 s 1 s_1 s1和 s 2 s_2 s2来对 x 1 x_1 x1进行全局量化,并在以 x 1 x_1 x1为中心的邻域内对 x 2 x_2 x2进行量化。
收缩路径具有九个卷积层,并且每个卷积层后面跟着ReLU激活函数,其中6个卷积层的步长为2。没有全连接层,这样网络可以接受任意大小的输入图像。第一个卷积层的卷积核大小为 7 × 7 7\times7 7×7,第2,3个为 5 × 5 5\times5 5×5,后面的卷积核为 3 × 3 3\times3 3×3。收缩路径的具体结构如下图所示。
2. 扩张路径
pooling操作在CNN中是必要的,它可以让网络聚合较大区域的信息,但是pooling会导致分辨率降低。所以就需要对池化后的比较粗糙的表示(representation)进行改善。在FlowNet中是通过扩张路径来实现的。
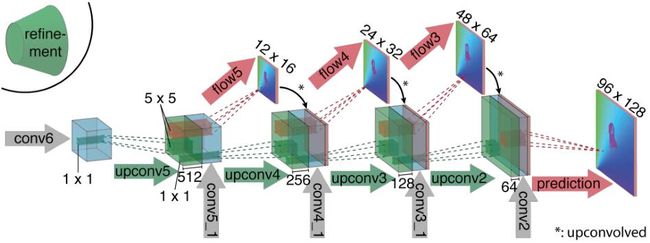
扩张路径主要由多个“上卷积(upconvolutional)”层组成,每个上卷积层包括一个unpooling(作为pooling操作的反操作,用来扩张特征图)和卷积操作。通过这种方式,既保留了来自粗糙特征图的高水平信息,又改善了低层特征图的局部信息。重复该过程四次,但最后的输出还是比原始大小小四倍。又由于更多的分辨率改善并不能提升效果,所以就直接使用双线性上采样来恢复到原始输入大小。扩张路径的结构如下图所示。
作者还使用了变分的方法来代替以上双线性上采样的方法,即先用20次迭代将流场恢复到原始大小,然后在全图像分辨率下再运行5次迭代,并计算图像边界,通过 α = exp ( − λ b ( x , y ) κ ) \alpha=\exp \left(-\lambda b(x, y)^{\kappa}\right) α=exp(−λb(x,y)κ)替换平滑系数来重新检查检测到的边界,其中 b ( x , y ) b(x,y) b(x,y)表示在各自的尺度和像素间重采样的薄边界强度。这种方式计算量更大,但是可以获得光滑的亚像素级的精确流场。下面会用一个“+v”的后缀来表示使用这种变分方法得到的结果。下图是采用变分法和FlowNetS的实验结果对比,前者会更好一点。
三、实验
1. 数据集
使用的已有数据集有Middlebury数据集、KITTI数据集和MPI Sintel数据集(分为Clean和Final两种),并通过仿射变换生成了一个新的合成数据集Flying Chairs。下图是每个数据集的情况。
并且使用了数据增强来增加训练集大小,具体的使用了仿射变换(平移,旋转,缩放,添加高斯噪声,改变亮度、对比度、gamma值和颜色)。下图是数据增强前后的对比图。
2. 训练设置
FlowNetC中的关联层中选用参数 k = 0 , d = 20 , s 1 = 1 , s 2 = 2 k=0,d=20,s_1=1,s_2=2 k=0,d=20,s1=1,s2=2。使用端点误差(endpoint error,EPE)作为训练的损失函数,它表示预测的流向量和ground truth之间每个像素平均的欧几里得距离。
选用Adam作为优化器,参数为 β 1 = 0.9 , β 2 = 0.999 \beta_1=0.9,\beta_2=0.999 β1=0.9,β2=0.999,mini-batch size为8个图像对,学习率为 1 e − 4 1e^{-4} 1e−4,在前300k轮迭代后没经过100k次迭代学习率衰减为上次的一半。在FlowNetC中,学习率设为 1 e − 6 1e^{-6} 1e−6,以防止梯度爆炸,并在10k次迭代后让学习率缓慢接近 1 e − 4 1e^{-4} 1e−4。
在正式使用模型时,需要在目标数据集上进行微调,即以学习率 1 e − 6 1e^{-6} 1e−6学习几千次。后面将用“-ft”的后缀表示使用了微调的模型。
3. 实验结果
下图是各个方法在不同数据集上的实验结果对比图。FlowNetC似乎对大的位移预测有问题。
下图是实验可视化的结果。