数据挖掘——工业蒸汽量预测

一、赛题描述

经脱敏后的锅炉传感器采集的数据（采集频率是分钟级别），根据锅炉的工况，预测产生的蒸汽量。赛题链接：
工业蒸汽量预测-天池大赛-阿里云天池

二、数据说明

数据分成训练数据（train.txt）和测试数据（test.txt），其中字段”V0”-“V37”，这38个字段是作为特征变量，”target”作为目标变量。选手利用训练数据训练出模型，预测测试数据的目标变量，排名结果依据预测结果的MSE（mean square error）。

三、导入相关库

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from scipy.stats import kstest
from scipy import stats
from sklearn.decomposition import PCA

• 知识点1
  matplotlib.pyplot库和seaborn库一般联合使用，可以创建多个子画布

四、读取文件

# 训练集、测试集文件位置
train_data_file = './data/zhengqi_train.txt'
test_data_file = './data/zhengqi_test.txt'
# 读取训练集和测试集合
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')

• 知识点2
  pandas库的read_csv函数都可以读取csv、txt、excel文件等。
  read_csv函数的参数详解见资料：
  Pandas：外部文件数据导入/读取

五、数据处理

5.1. 缺失值处理

print(train_data.info())
print(train_data.columns)
print(test_data.info())
print(test_data.columns)
# 通过以上结果，可以看出，没有缺失值

• 知识点3
  DataFrame.info()可以显示是否有缺失值情况以及各个变量的类型,具体参数如下：
  DataFrame.info(verbose=None, buf=None, max_cols=None, memory_usage=None, null_counts=None)
  verbose：是否要打印完整的摘要。当变量非常多的时候，可以令verbose=False显示简要摘要
  null_counts：是否显示非空计数，即可以显示各个变量的缺失值

5.2. 异常值处理

将训练集和测试集的X合并，探索总体分布情况，进而划定异常值标准。

data_all_X = pd.concat([train_data.drop(['target'], axis=1), test_data], axis=0)
plt.figure(figsize=(18,10))
plt.boxplot(x=data_all_X.values, labels=data_all_X.columns)
plt.show()

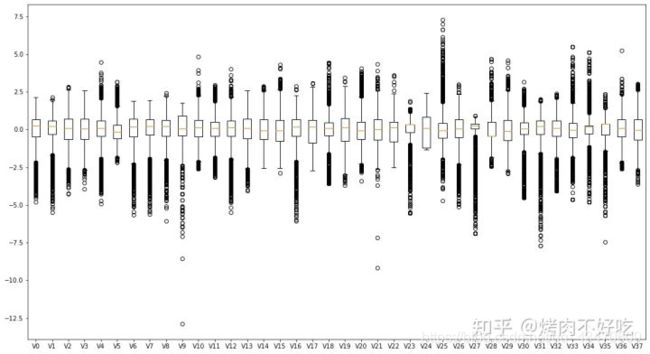
从上面的箱型图可以看出，“V9”、“V21”、“V35”、“V36”四个变量存在比较明显的异常值。

# 训练集和测试集的异常值，用除去异常值后的最大值/最小值进行填补
V9_min = data_all_X[data_all_X['V9']>-7.5]['V9'].min()
V21_min = data_all_X[data_all_X['V21']>-5]['V21'].min()
V35_min = data_all_X[data_all_X['V35']>-7]['V35'].min()
V36_max = data_all_X[data_all_X['V36']<5]['V36'].max()
print(V9_min, V21_min, V35_min, V36_max)

def change_v9(x):
    if x <= -7.5:
        return -7.071
    else:
        return x


def change_v21(x):
    if x <= -5:
        return -3.6889999999999996
    else:
        return x


def change_v35(x):
    if x <= -7:
        return -5.695
    else:
        return x


def change_v36(x):
    if x >= 5:
        return 3.372
    else:
        return x


train_data['V9'] = train_data['V9'].apply(lambda x: change_v9(x))
train_data['V21'] = train_data['V21'].apply(lambda x:change_v21(x))
train_data['V35'] = train_data['V35'].apply(lambda x:change_v35(x))
train_data['V36'] = train_data['V36'].apply(lambda x:change_v36(x))

test_data['V9'] = test_data['V9'].apply(lambda x: change_v9(x))
test_data['V21'] = test_data['V21'].apply(lambda x:change_v21(x))
test_data['V35'] = test_data['V35'].apply(lambda x:change_v35(x))
test_data['V36'] = test_data['V36'].apply(lambda x:change_v36(x))

训练集和测试集和的异常值处理完成

5.3.归一化处理

# 对训练集和测试集都进行归一化处理
min_max_scaler = MinMaxScaler()
columns = list(test_data)
scaler = min_max_scaler.fit(train_data.drop(['target'],axis=1)) # 用训练集的数据作为标准尺
train_data_scaler = pd.DataFrame(scaler.transform(train_data.drop(['target'],axis=1)))
test_data_scaler = pd.DataFrame(scaler.transform(test_data))

train_data_scaler.columns = columns
test_data_scaler.columns = columns
train_data_scaler['target'] = train_data['target']

• 知识点4
  class sklearn.preprocessing.MinMaxScaler()函数，其fit(X)、fit_transform(X)、transform(X)等属性函数，其X必须是array-like of shape类型。
  MinMaxScaler()的具体参数详解见链接：
  sklearn.preprocessing.MinMaxScaler - scikit-learn 0.24.1

六、特征工程

6.1 训练集和测试集中变量的分布一致性分析

dist_cols = 6
dist_rows = 7

plt.figure(figsize=(4*dist_cols, 4*dist_rows))
i = 1
for col in test_data_scaler.columns:
    ax = plt.subplot(dist_rows, dist_cols, i)
    ax = sns.kdeplot(train_data_scaler[col], color='Red', shade=True)
    ax = sns.kdeplot(test_data_scaler[col], color='Blue', shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel('Frequency')
    ax = ax.legend(['train','test'])
    i = i + 1
plt.show()

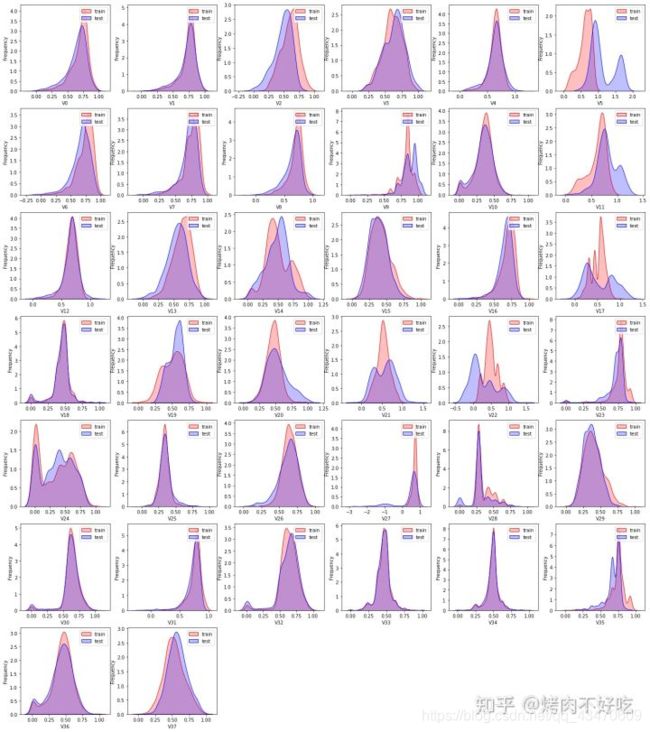
【matplotlib.pyplot库与seaborn库的结合使用。用ax=plt.subplot()创建子画布，然后ax=sns.kde()进行绘图】
通过上面的KDE图，可以看出V5、V11、V17、V22这四个变量，在训练集和测试集上的分布及其不一致，对模型的泛化能力有影响，所以在训练集和测试集中将这四个变量进行删除。

dropList = ['V5','V11','V17','V22']
train_data_scaler2 = train_data_scaler.drop(dropList, axis=1) #注意，DataFrame.drop()函数，删除列时，参数axis=1不可省略，且列需要用列表进行表示。
test_data_scaler2 = test_data_scaler.drop(dropList, axis=1)

6.2 特征相关性分析

6.2.1 特征与target之间的pearson线性相关系数

• 知识点6
  Pearson系数指变量间的线性相关系数，其数据类型需要是数值型与数值型之间的关系，并且使用该系数还需验证数据服从于正态分布。
  Pearson、Spearman等相关系数的介绍详细见资料：
  利用dataframe的corr()计算相关系数
  通过上面的KDE分布图，可以看出大部分特征的分布都不属于正态分布，因此计算pearson系数前，需要先进行正态分布转换；

（1）对训练集进行正态分布判断

corr_data = train_data_scaler2.copy()
columns_list = list(corr_data)
for column in columns_list:
    print(column, kstest(corr_data[column], 'norm'))

• 知识点7
  KS检验、T检验、卡方检验的资料链接：
  假设检验–KS检验、t检验、卡方检验

从各个特征的P值来看，都不符合正态分布，所以需要进行正态分布变换后，再计算pearson相关系数。
（2）正态分布变换

columns = list(corr_data)
fcols = 6
frows = len(columns)

plt.figure(figsize=(4*fcols, 4*frows))
i = 0

corrPearson_dict = {}
for var in columns:
    if var != 'target':
        dat = corr_data[[var, 'target']]
        i = i + 1
        plt.subplot(frows, fcols, i)
        sns.distplot(dat[var], fit=stats.norm)
        plt.title(var + ' Original')
        plt.xlabel('')
        plt.ylabel('')
    
        i += 1
        plt.subplot(frows, fcols, i)
        _ = stats.probplot(dat[var], plot=plt) # 默认是检测正态分布
        plt.title('skew= ' + '{:.4f}'.format(stats.skew(dat[var])))  # stats.skew()函数计算偏度
        plt.xlabel('')
        plt.ylabel('')
    
        i += 1
        plt.subplot(frows, fcols, i)
        plt.plot(dat[var], dat['target'], '.', alpha=-0.5)
        plt.title('corr= ' + '{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))  # 注意np.corrcoef()函数返回的是一个相关系数矩阵
    
        i += 1
        plt.subplot(frows, fcols, i)
        trans_var, lambda_var = stats.boxcox(dat[var]+1)  # ＋1是为了防止出现负数, 这里返回的trans_var是ndarray
#     print(trans_var.reshape(-1,1))
#     print(pd.DataFrame(trans_var))
        trans_var = pd.DataFrame(MinMaxScaler().fit_transform(trans_var.reshape(-1,1)))[0]  # 变换的原因是MinMaxScaler().fit_transform要求输入是二维数组
        sns.distplot(trans_var, fit=stats.norm)
        plt.title(var + ' Transformed')
        plt.xlabel('')
        plt.ylabel('')
    
        i += 1
        plt.subplot(frows, fcols, i)
#     print(trans_var)
        _ = stats.probplot(trans_var, plot=plt)
        plt.title('skew= ' + '{:.4f}'.format(stats.skew(trans_var)))
        plt.xlabel('')
        plt.ylabel('')
    
        i += 1
        plt.subplot(frows, fcols, i)
        plt.plot(trans_var, dat['target'], '.', alpha=-0.5)
        corrPearson = np.corrcoef(trans_var, dat['target'])[0][1]
        plt.title('corr= ' + '{:.2f}'.format(corrPearson))
        
        corrPearson_dict[var] = corrPearson

• 知识点8
  box_cox()变换来明显地改善数据的正态性、对称性和方差相等性。资料见：
  BoxCox以及反变换的简介和Python实现
• 知识点9
  Q-Q图：适用于检验分布。具体内容见资料：
  QQ图 分位图理解 python实现

sorted(corrPearson_dict.items(), key=lambda x:x[1], reverse=True)  # 线性相关性排序

• 知识点10
  stats.skew()偏度的意义与计算。资料见：
  偏度与峰度的正态性分布判断
• 知识点11
  sorted()函数知识点，对所有可迭代对象进行排序操作。详细参数解释见资料：
  python sorted()函数

6.2.2 特征及target间的spearman相关性热力图

为了快速，不需要进行正太变换的数据，直接使用源数据进行计算即可。

# 计算训练集的特征变量及与target变量之间的线性相关系数并绘制热力图
train_corr = train_data_scaler2[['V0','V1','V8','V27','V31','V2','V4','V12','V3','V16','V20','V10','V6','V36','V7','target']].corr(method='spearman')
ax = plt.subplots(figsize=(10,8))
ax = sns.heatmap(train_corr, square=True, annot=True, cmap='Reds')

通过相关性热力图可以看到，特征之间还是存在比较大的共线性。

6.3 PCA降维

# 保留90%的信息
pca = PCA(n_components=0.9)
train_pca_90 = pca.fit_transform(train_data_scaler2.iloc[:,0:-1])  # 注意，pca返回的是ndarray对象
test_pca_90 = pca.fit_transform(test_data_scaler2)

train_pca_90_df = pd.DataFrame(train_pca_90)
train_pca_90_df['target'] = train_data_scaler2['target']
test_pca_90_df = pd.DataFrame(test_pca_90)

七、模型训练

7.1 基于PCA降维后的数据

from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR
import lightgbm as lgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

model_train_data = train_pca_90_df.drop(['target'], axis=1)
model_train_label = train_pca_90_df['target']

# 切分数据集
model_train_x, model_val_x, model_train_y, model_val_y = train_test_split(model_train_data, 
                                                                          model_train_label, 
                                                                          test_size=0.2, random_state=0)

clf_LinR = LinearRegression()
clf_KnnR = KNeighborsRegressor()
clf_RF = RandomForestRegressor()
clf_dict = {'LinearRegression':clf_LinR, 'KNeighborsRegressor': clf_KnnR, 'RandomForestRegressor': clf_RF}
for key, value in clf_dict.items():
    clf = value
    clf.fit(model_train_x, model_train_y)
    score_train = mean_squared_error(model_train_y, clf.predict(model_train_x))
    score_val = mean_squared_error(model_val_y, clf.predict(model_val_x))
    print(key,'_train_score: ',score_train, ', ', key,'_val_score: ',score_val )

# lgb回归模型
clf = lgb.LGBMRegressor(
    learning_rate=0.01,
    max_depth=-1,
    n_estimators=5000,
    boosting_type='gbdt', 
    random_state=2019,
    objective='regression'
)
clf.fit(model_train_x, model_train_y, eval_metric='MSE', verbose=50)
score_train = mean_squared_error(model_train_y, clf.predict(model_train_x))
score_val = mean_squared_error(model_val_y, clf.predict(model_val_x))
print('LightGBM_trainScore: ', score_train)
print('LightGBM_valScore: ', score_val)

LinearRegression _train_score: 0.13546364510120967 ,
LinearRegression _val_score: 0.1443726103513309；
KNeighborsRegressor _train_score: 0.12276401908225111 ,
KNeighborsRegressor _val_score: 0.1891955407612457；
RandomForestRegressor _train_score: 0.020359722055367967 ,
RandomForestRegressor _val_score: 0.15518873117871973；
LightGBM_trainScore: 0.0005286116914398528
LightGBM_valScore: 0.14779041329036227；

7.2 基于未进行PCA降维的数据

model_train_data = train_data_scaler2.drop(['target'], axis=1)
model_train_label = train_data_scaler2['target']

# 切分数据集
model_train_x, model_val_x, model_train_y, model_val_y = train_test_split(model_train_data, 
                                                                          model_train_label, 
                                                                          test_size=0.2, random_state=0)
clf_LinR = LinearRegression()
clf_KnnR = KNeighborsRegressor()
clf_RF = RandomForestRegressor()
clf_dict = {'LinearRegression':clf_LinR, 'KNeighborsRegressor': clf_KnnR, 'RandomForestRegressor': clf_RF}
for key, value in clf_dict.items():
    clf = value
    clf.fit(model_train_x, model_train_y)
    score_train = mean_squared_error(model_train_y, clf.predict(model_train_x))
    score_val = mean_squared_error(model_val_y, clf.predict(model_val_x))
    print(key,'_train_score: ',score_train, ', ', key,'_val_score: ',score_val )

# lgb回归模型
clf = lgb.LGBMRegressor(
    learning_rate=0.01,
    max_depth=-1,
    n_estimators=5000,
    boosting_type='gbdt', 
    random_state=2019,
    objective='regression'
)
clf.fit(model_train_x, model_train_y, eval_metric='MSE', verbose=50)
score_train = mean_squared_error(model_train_y, clf.predict(model_train_x))
score_val = mean_squared_error(model_val_y, clf.predict(model_val_x))
print('LightGBM_trainScore: ', score_train)
print('LightGBM_valScore: ', score_val)

LinearRegression _train_score: 0.10737730560413991 ,
LinearRegression _val_score: 0.12068756183502802；
KNeighborsRegressor _train_score: 0.12693217080519478 ,
KNeighborsRegressor _val_score: 0.19089168325259517；
RandomForestRegressor _train_score: 0.017473277313419907 ,
RandomForestRegressor _val_score: 0.13327670324878893；
LightGBM_trainScore: 0.00010676910117809182，
LightGBM_valScore: 0.11518232686929555；

发现不降维的MSE更小，可能由于数据量不大，变量保留越多，训练效果更优。选择MSE最小的LightGBM模型作为最终模型，进行5折交叉验证。

7.3 LightGBM交叉验证

from sklearn.model_selection import KFold

# 5折交叉验证
folds = 5
kf = KFold(n_splits=folds, shuffle=True, random_state=2019)
# 记录训练和验证的MSE评估值
mse_dict = {'train_score':[], 'val_score':[]}

for i, (train_index, val_index) in enumerate(kf.split(model_train_data)):
    # lgbm模型
    lgb_reg = lgb.LGBMRegressor(
        learning_rate=0.01,
        max_depth=-1,
        n_estimators=5000,
        boosting_type='gbdt', 
        random_state=2019,
        objective='regression'
    )
    
    # 训练集和验证集划分
    x_train, x_val = model_train_data.values[train_index], model_train_data.values[val_index]
    y_train, y_val = model_train_label.values[train_index], model_train_label.values[val_index]
    
    # 训练模型
    lgb_reg.fit(X=x_train,
                y=y_train,
                eval_set = [(x_train, y_train),(x_val, y_val)],
                eval_names = ['Train', 'Test'],
                early_stopping_rounds = 100,
                eval_metric = 'MSE',
                verbose=50
               )
    # 预测结果
    y_train_pred = lgb_reg.predict(x_train)
    y_val_pred = lgb_reg.predict(x_val)
    
    
    # 输出结果
    print('第{}折 训练和验证，输出训练和验证集的MSE值'.format(i+1))
    train_mse = mean_squared_error(y_train_pred, y_train)
    val_mse = mean_squared_error(y_val_pred, y_val)
    print('训练MSE： ', train_mse)
    print('验证MSE： ', val_mse)
    print('---------------------')
    
    mse_dict['train_score'].append(train_mse)
    mse_dict['val_score'].append(val_mse)

print('train_Scroe: ',mse_dict['train_score'])
print('mean: ',np.mean(mse_dict['train_score']))
print('val_Score: ', mse_dict['val_score'])
print('mean: ', np.mean(mse_dict['val_score']))

train_Scroe: [0.0032434256043935455, 0.0048461436966905705, 0.014306183584510147, 0.006993800192889838, 0.012536588494285968]；
mean: 0.008385228314554013

val_Score: [0.10270513472418036, 0.1316075425412059, 0.10190565968024304, 0.11005801498826165, 0.09958963890283057]；
mean: 0.1091731981673443

7.4 测试集预测

test_data_scaler2

lgb_reg = lgb.LGBMRegressor(
        learning_rate=0.01,
        max_depth=-1,
        n_estimators=5000,
        boosting_type='gbdt', 
        random_state=2019,
        objective='regression'
    )

lgb_reg.fit(X=model_train_data,
            y=model_train_label,
            eval_set = [(model_train_data, model_train_label)],
            early_stopping_rounds = 100,
            eval_metric = 'MSE',
            verbose=50
           )
# 预测结果
y_test_pred = lgb_reg.predict(test_data_scaler2)

with open('./data/pred_result.txt', 'w', encoding='utf-8') as f:
    for i in y_test_pred:
        f.write(str(i)+'\n')

八、缺陷

• 没有调参。调参前，如何确定参数的选择范围？
• 没有进行更为复杂的特征变换。对于特征变换，针对该应用场景，有什么具体的思路？
• 没有进行模型融合，还没学…

数据挖掘小白，各路大神请多多指教，不胜感激！！！