算法系列-计数排序
计数排序是一种算法复杂度 O(n) 的排序方法,适合于小范围集合的排序。比如100万学生参加高考,我们想对这100万学生的数学成绩(假设分数为0到100)做个排序。我们如何设计一个最高效的排序算法。本文不光给出计数排序算法的传统写法,还将一步步深入讨论算法的优化,直到时间复杂度和空间复杂度最优。
先看看计数排序的定义
Counting sort (sometimes referred to as ultra sort or math sort[1]) is a sorting algorithm which (like bucket sort) takes advantage of knowing the range of the numbers in the array to be sorted (array A). It uses this range to create an array C of this length. Each index i in array C is then used to count how many elements in A have the value i; then counts stored in C can then be used to put the elements in A into their right position in the resulting sorted array. The algorithm was created by Harold H. Seward in 1954.
计数排序是一个类似于桶排序的排序算法,其优势是对已知数量范围的数组进行排序。它创建一个长度为这个数据范围的数组C,C中每个元素记录要排序数组中对应记录的出现个数。这个算法于1954年由 Harold H. Seward 提出。
下面以示例来说明这个算法
假设要排序的数组为 A = {1,0,3,1,0,1,1}
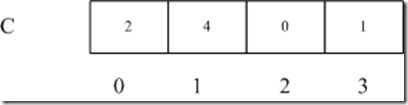
这里最大值为3,最小值为0,那么我们创建一个数组C,长度为4.
然后一趟扫描数组A,得到A中各个元素的总数,并保持到数组C的对应单元中。
比如0 的出现次数为2次,则 C[0] = 2;1 的出现次数为4次,则C[1] = 4
由于C 是以A的元素为下标的,所以这样一做,A中的元素在C中自然就成为有序的了,这里我们可以知道 顺序为 0,1,3 (2 的计数为0)
然后我们把这个在C中的记录按每个元素的计数展开到输出数组B中,排序就完成了。
也就是 B[0] 到 B[1] 为0 B[2] 到 B[5] 为1 这样依此类推。
这种排序算法,依靠一个辅助数组来实现,不基于比较,算法复杂度为 O(n) ,但由于要一个辅助数组C,所以空间复杂度要大一些,由于计算机的内存有限,这种算法不适合范围很大的数的排序。
注:基于比较的排序算法的最佳平均时间复杂度为 O(nlogn)
Counting sort
Depends on a key assumption: numbers to be sorted are integers in{0, 1, . . . , k}.
Input: A[1 . . n], where A[ j ] ∈ {0, 1, . . . , k} for j = 1, 2, . . . , n. Array A and
values n and k are given as parameters.
Output: B[1 . . n], sorted. B is assumed to be already allocated and is given as a
parameter.
Auxiliary storage: C[0 . . k]
8-4 Lecture Notes for Chapter 8: Sorting in Linear Time
COUNTING-SORT(A, B, n, k)
for i ← 0 to k
do C[i ] ← 0
for j ← 1 to n
do C[A[ j ]] ← C[A[ j ]] + 1
for i ← 1 to k
do C[i ] ← C[i ] + C[i − 1]
for j ← n downto 1
do B[C[A[ j ]]] ← A[ j ]
C[A[ j ]] ← C[A[ j ]] − 1
Do an example for A = 21, 51, 31, 01, 22, 32, 02, 33
Counting sort is stable (keys with same value appear in same order in output as
they did in input) because of how the last loop works.
上面这段引自麻省理工大学计算机算法教材的技术排序部分,我不做翻译了。这个就是这个算法的典型解法,我把它作为方案1.
这个算法的实际扫描次数为 n+k (不包括写的次数)
方案1
public static void Sort(int[] A, out int[] B, int k)
{
Debug.Assert(k > 0);
Debug.Assert(A != null);
int[] C = new int[k + 1];
B = new int[A.Length];
for (int j = 0; j < A.Length; j++)
{
C[A[j]]++;
}
for (int i = 1; i <= k; i++)
{
C[i] += C[i-1];
}
for (int j = A.Length - 1; j >= 0; j--)
{
B[C[A[j]]-1] = A[j];
C[A[j]]--;
}
}
上面代码是方案1 的解法,也是计数排序算法的经典解法,麻省的教材上也是这样解。不过这个解法并不是最优的,因为空间复杂度还应该可以优化,我们完全可以不要那个输出的数组B,直接对A进行排序。在继续看方案2之前,我建议大家先自己思考一下,看看是否有办法省略掉数组B
方案2
我们对上述代码进行优化
public static void Sort(int[] A, int k) { Debug.Assert(k > 0); Debug.Assert(A != null); int[] C = new int[k + 1]; for (int j = 0; j < A.Length; j++) { C[A[j]]++; } int z = 0; for (int i = 0; i <= k; i++) { while (C[i]-- > 0) { A[z++] = i; } } }
由于C数组下标 i 就是A 的值,所以我们不需要保留A中原来的数了,这个代码减少了一个数组B,而且要比原来的代码简化了很多。
和快速排序的速度比较
拿本文刚开始那个高考成绩的例子来做
int[] A = new int[1000000];
int[] B = new int[1000000];
Random rand = new Random();
for (int i = 0; i < A.Length; i++)
{
A[i] = rand.Next(0, 100);
}
A.CopyTo(B, 0);
Stopwatch sw = new Stopwatch();
sw.Start();
Array.Sort(B);
sw.Stop();
Console.WriteLine(sw.ElapsedMilliseconds);
sw.Reset();
sw.Start();
CountingSort.Sort(A, 100);
sw.Stop();
Console.WriteLine(sw.ElapsedMilliseconds);
输出结果
134 //快速排序
18 //计数排序
可见计数排序要比快速排序快将近6倍左右。