《机器学习》阅读笔记 第三章

1. 不同学科中的线性模型¹

第三章主要介绍线性模型。线性模型在传统的统计学、计量经济学和机器学习中都是很常用的模型，但是关注点不同。比如说，计量经济学中，主要关注线性模型的参数估计量之解释，从而阐释经济理论或者进行因果推断，因此，在计量中学线性回归，我们主要学的是参数估计量性质、统计检验、回归诊断及针对不同类型数据（截面、时序、面板、受限因变量）的处理办法等，而不太关注模型对于新数据的预测能力（时序预测部分除外）；而机器学习中则关注线性模型对于外样本的预测精度，对于统计量性质等则不怎么关心。

更进一步来说，传统计量经济学中的模型设定是基于经济理论的，目的是解释经济理论中变量间的关系，完成实证研究；而机器学习的模型设定是基于数据的，目的是探寻数据中未被发现的规律，因此只要模型能达到比较好的预测精度，是否有相应的理论做支撑（看起来）似乎不太重要。当然，现在可解释学习、因果推断等也是机器学习研究的前沿，但是就这本《机器学习》中介绍的线性模型来看，还是以提升精度、抗过拟合为主的。

既然已经有一学期的计量作为基础，线性模型的基本形式和最小二乘解部分内容就不再详细记录了，只是提纲挈领；对数几率回归部分主要比较计量课上学的Logit模型（就是对数几率回归）与西瓜书的不同讲述方式；线性判别分析和多分类问题处理办法是新的内容，会记录得比较多。

2. 线性模型：回归任务

2.1 估计方法

模型是
$$y=\mathbf{X}w$$

估计方法至少有OLS、MLE、MM三种，就基本多元线性回归来看，在 ${\mathbf{X}}^{\prime }\mathbf{X}$ 满秩的情况下，统一的解是

$$\hat{w}=({\mathbf{X}}^{\prime }\mathbf{X}{)}^{-1}{\mathbf{X}}^{\prime }y$$

另外，这部分有一个离散解释变量数值化的问题，关键是不存在序关系的离散解释变量不能直接赋整数值（因为整数值是带序关系的，会误导模型），应该采用one-hot编码的方式，将其转换为线性无关的向量，每个向量只有一位取1，其余取0，这个方法和计量中的哑变量是类似的，注意向量数（哑变量个数）应为离散应变量类别数-1，作为基准的那一类取全0即可，节约空间的同时缓解了估计中可能产生的多重共线性问题。

2.2 正则化

在OLS回归中，如果 ${\mathbf{X}}^{\prime }\mathbf{X}$ 不满秩，则无法通过求逆矩阵来得出最小二乘解。就是说，这是一个“稀疏”的问题：特征数大于样本容量（这是大数据的一个典型特征），使得线性方程组的解无法唯一确定。为了解决这一问题，可以设定特定的归纳偏好，或者引入正则项。所谓正则项，就是在线性模型的均方误差表达式中加入一个惩罚项，比如说，岭回归（ridge regression）就是加入 ${\mathcal{L}}_2$ 范数作为正则项：

$$\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\sum _{i=1}^m(y_i-w^{\prime }{x}_i{)}^2+\lambda ||w|{|}_2^2\text{\hspace{1em}(1)}$$

而LASSO就是加入 ${\mathcal{L}}_1$ 范数作为正则项：

$$\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\sum _{i=1}^m(y_i-w^{\prime }{x}_i{)}^2+\lambda ||w|{|}_1\text{\hspace{1em}(2)}$$

正则项能够起到选择变量、缓解过拟合的效果，从而解决稀疏问题。从直观上看，当正则化参数 $\lambda$ 比较大时，最小化 $(1)$ 或 $(2)$ 式很大程度就变成了最小化正则项，而最小化正则项自然就要求某些 $w_i=0$，这就在做优化的过程中将一些属性删去了，起到了变量选择的作用。当然这一直观背后的优化理论证明是比较复杂的（笔者也不懂），这里只是做一个简单的解释。

还可以从约束优化的角度去理解正则项的作用。不太严格地说，如果将 $\lambda$ 看作拉格朗日乘子，那么 $(1)$ 式等价于：

$$\begin{gathered} \mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\sum _{i=1}^m(y_i-w^{\prime }{x}_i{)}^2 \\ \mathrm{s}.\mathrm{t}.||w|{|}^2\le t \end{gathered}$$

这里，目标函数和约束函数都是关于 $w$ 的二次函数，可以大致在平面上画出其等高线（或约束函数的函数图像）（如下图）：

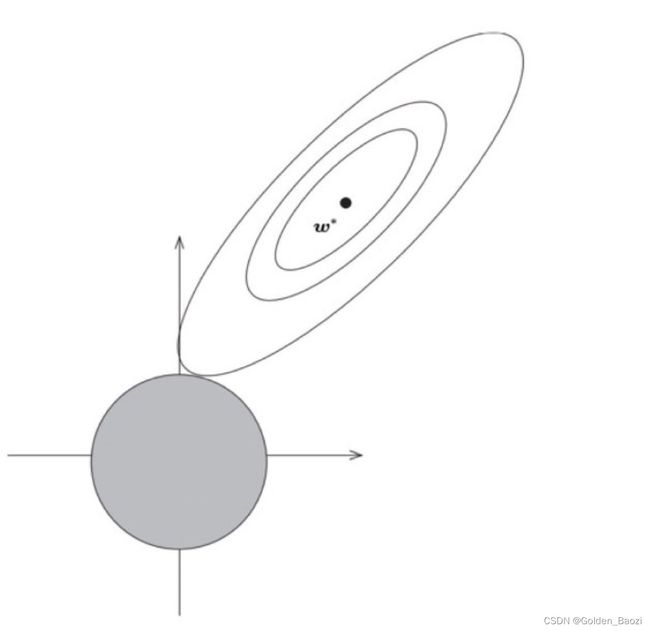
根据约束优化的一阶必要条件（常用的是KKT条件），最优解应该在约束式起作用的位置，也就是约束函数等高线的边界上。在图上展示，就是目标函数等高线与约束函数相切的位置，可以发现，最优解在某一个维度上的取值（相比于无约束的最优解）十分接近0。

那么，如何求优化问题 $(1)$ 或 $(2)$ 式 的解呢²？需要采用一些数值方法。问题 $(1)$ 是一个凸优化问题，可以采用经典的（一阶）梯度下降算法或者二阶的（拟）牛顿法，简单来说，就是利用泰勒展开得到的一阶或者二阶导数信息来近似目标函数，从而更新初始点，按照这个过程一直迭代下去，直到已知的解变化很小（十分接近最优点）为止，当然，这其中涉及到如何保证算法的下降性、收敛性等的问题。而问题 $(2)$ 是一个凸与非凸函数组合的复合优化问题，可以用坐标下降法、近似点梯度法、或者交替方向乘子法（ADMM）求解。

正则化其实也可以看作一种变量选择方法，其余回归中常用的变量选择方法还有手动筛选变量、逐步回归等。《机器学习》第11章主要关注这部分内容。再插一句，在计量经济学的视角下，加入正则项还能起到缓解多重共线性的作用。

2.3 广义线性模型

对基本线性模型

$$y=w^{\prime }x+b$$

右侧套上不同的非线性函数 $g(\cdot )$，就可以造出一些非线性模型来拟合 $y$。常用的如书中在下一节介绍了对数几率回归，就是取 $g(\cdot )$ 为

$$g(x)=\frac{1}{1+e^{-x}}$$

此外，还有在计量中常用的泊松回归、负二项回归，以及神经网络（本质上是做多次线性组合+非线性变换）等，都是取了不同的非线性函数形式。

3. 线性模型：分类任务

3.1 对数几率回归

基本出发点是希望基于线性模型 $y=w^{\prime }x+b$ 做二分类，设定输出高于某个阈值时，分为正类，否则分为负类。又为了做优化方便，希望目标函数是一个光滑的函数，这样，对率函数

$$g(x)=\frac{1}{1+e^{-x}}$$

就被选中了，它可以将输出值压缩到 $(0,1)$ 之间，在分界位置处对输入敏感，无限阶可微，满足了我们的要求。接下来的过程，就是将对率函数套在线性模型上，建立求解方法（MLE），做优化，得到结果，过程是简单的。

如何解释对数几率回归呢？西瓜书中，作者先将 $g(\cdot )$ 套在线性模型上，再根据上一节中讨论的结果变换得到

$$\ln \frac{y}{1-y}=w^{\prime }x+b$$

进一步定义左式为对数几率，分别赋予分子分母概率含义，得到了概率分布列的表达式，进而用上MLE。可以归纳一下，这是一个公式（统计模型）$\to$ 理论的过程。

而在我上学期的计量课上，老师对于Logit模型的讲解则是一个经济理论 $\to$ 公式（统计模型）的过程。首先定义效用模型，记 $U_i^k$ 是个体 $i$ 选择 $k\in \{0,1\}$ 的效用，则可设定效用满足基本线性模型的形式，并做变换：

$$\begin{gathered} U_i^0=X_i{\beta }^0+{ϵ}_i^0 \\ {U}_i^1=X_i{\beta }^1+{ϵ}_i^1 \\ ⟹U_i^0-U_i^1=X_i({\beta }^1-{\beta }^0)+({ϵ}_i^1-{ϵ}_i^0) \\ ⟶Y_i^{\ast }=X_i\beta +{\mu }_i^{\ast } \end{gathered}$$

个体做出使它效用更高的选择，因此

$$P(Y_i=1)=P(Y_i^{\ast }>0)=P({\mu }_i^{\ast }>-X_i\beta )$$

进一步假设随机扰动项 ${\mu }_i^{\ast }$ 服从所谓的“Logit分布”（是否有这一说法？），即其累积分布函数是：

$$F_{{\mu }^{\ast }}(x)=\frac{1}{1+e^{-x}}$$

这样，就有

$$\begin{gathered} P(Y_i=1|X_i)=1-F_{{\mu }^{\ast }}(-X_i\beta )=\frac{e^{X_i\beta }}{1+e^{X_i\beta }} \\ P(Y_i=0|X_i)=1-P(Y_i=1|X_i)=\frac{1}{1+e^{X_i\beta }} \end{gathered}$$

从而可使用MLE，也可定义对率，研究参数 $\beta$ 的经济含义。只要注意一下，$Y_i$ 的分布函数可以写成

$$Y_{i}P(Y_i=1|X_i)+(1-Y_i)P(Y_i=0|X_i)$$

线性判别分析（LDA）³

LDA的思路也很简单：将样本点映射到一条直线上（做一个线性变换），找这样一条直线，使映射后的样本点类间距离最大，类内散度最小，从而将两类样本“分开”。关键是理解类内距离和类间距离是如何表达的。

设某个样本的特征是 $x_i$，两类样本特征的均值向量分别是 ${\mu }_0,{\mu }_1$，协方差矩阵是 ${\Sigma }_0,{\Sigma }_1$，以类别 $y_i=0$ 为例，有

$$\begin{array}{rl}{\mu }_0& =\frac{1}{|X_0|}\sum _{i\in X_0}{x}_i\\ {\Sigma }_0& =\frac{1}{|X_0|-1}\sum _{i\in X_0}(x_i-{\mu }_0)(x_i-{\mu }_0{)}^{\prime }\end{array}$$

变换后，有 $x_i^{\ast }=w^{\prime }{x}_i$ ，以及

$$\begin{array}{rl}{\mu }_0^{\ast }& =w^{\prime }{\mu }_0\\ {\Sigma }_0^{\ast }& =w^{\prime }{\Sigma }_{0}w\end{array}$$

接下来手写了⁴

多分类的基本思路

基本思路是用多个二分类，然后投票。$\mathrm{O}\mathrm{v}\mathrm{O}$ 和 $\mathrm{O}\mathrm{v}\mathrm{R}$ 都好理解，主要记录一下自己对 $\mathrm{M}\mathrm{v}\mathrm{M}$ 中ECOC编码的理解。

以图3.5(a)为例，5个分类器将4个类别按不同方式划分为正例和负例进行训练：

	f1	f2	f3	f4	f5
C1	-1	1	-1	1	1
C2	1	-1	-1	1	-1
C3	-1	1	1	-1	1
C4	-1	-1	1	1	-1
new	-1	-1	1	-1	1

比如说，分类器f1将类别2作为负类，其余类别作为正类进行训练。这五个分类器的划分方式对每一类形成了一个ECOC编码。现在来了新样本new，放到5个分类器中分别做预测，结果也在上图中展示了，将其预测结果组成一个向量，和4个类别的编码向量分别去计算距离，到哪一类的编码向量距离最短，就认为这个新样本属于哪一类。

ECOC码具有纠错能力是因为：当编码长度较长时，某一个位置分类错误不会影响整个编码的距离计算，就像一个极限为无穷的级数，去掉前面有限项后，剩余部分的极限还是无穷。NFL定理对于ECOC编码问题依然适用，比如说纠错效果越好的ECOC编码需要更多的训练开销。

---

1. 这一节及之后关于计量经济学的内容来自我上学期上的计量课，如有理解错误的地方，一定是因为我的水平不够。我用的教材是《计量经济学》（李子奈）。关于计量和机器学习中线性模型比较的部分参考了“Big Data: New Tricks for Econometrics”（Hal Varian） ↩︎

2. 关于优化算法的内容参考了《数值最优化方法》（高立） ↩︎

3. 当心一下，潜在迪利克雷分配（用来做文本聚类的那个）也叫LDA ↩︎

4. 参考了南瓜书第三章 ↩︎