进化算法和深度强化学习的关系？

目录

一、前言

二、进 化 算 法 引 导 策 略 搜 索 的 强 化 学 习

1.参 数 分 布 搜 索 方 法

2.策 略 梯 度 近 似 方 法

3.策 略 种 群 搜 索 方 法

三、进 化 算 法 经 验 指 导 的 深 度 强 化 学 习

1.无 反 馈 的 指 导

2.有 反 馈 的 指 导

3.进 化 算 法 模块嵌入 的 深 度 强 化 学 习

四、总 结 与 展 望

---

一、前言

深 度 强 化 学 习 是 目 前 机 器 学 习 领 域 中 重 要 的 研 究 分 支 之 一 ， 它 可 以 通 过 直 接 与 环 境 进 行 交 互 实 现 端 到 端 的 学 习 ， 对 高 维 度 和 大 规 模 的 问 题 有 着 很 好 的 解 决 能 力 ． 虽 然 深 度 强 化 学 习 已 经 取 得 了 瞩 目 的 成 果 ， 但 其 仍 面 临 着 对 环 境 探 索 能 力 不 足 、 鲁 棒 性 差 、 容 易 受 到 由 欺 骗 性 奖 励 导 致 的 欺 骗 性 梯 度 影 响 等 问 题 ．

进 化 算 法 普 遍 具 有 较 好 的 全 局 搜 索 能 力 、 良 好 的 鲁 棒 性 和 并 行 性 等 优 点 ， 因 此 将 进 化 算 法 与 深 度 强 化 学 习 结 合 用 于 弥 补 深 度 强 化 学 习 不 足 的 方 法 成 为 了 当 前 研究 的 热 点。在 强 化 学 习 中 ， 也 可 以 使 用 进 化 算 法 选 择 其 超 参 数 或 优 势 个 体。

 进 化 算 法 结合到 深度 强 化学 习 算 法 之 中 时 ， 进 化 算法 中 的 个 体通 常 作 为 深度强 化  中 的 策 略 网 络 ， 种 群 则 是 由 多 个策 略 网 络 所 组 成 的 网 络 集 合 ， 而进 化 算 法中 对 个体 的 交叉 与变异操 作 则 对应策 略 网 络参数 的 交 叉 与 变 异 ， 在 深度 强 化学 习 中 评 估 某 个 个 体 的 策 略 网 络 的 方 法是 让其与 环 境进行交 互 ， 并 将交互 一 回 合所 获得 的 累 计 回 报看作 此 个体对 坏 境 的 适应度 。

融合两种方法的优点方式可分为进 化 算 法 引 导 策 略 搜 索 的 强 化 学 习 和 结 合 进 化 算 法 的 深 度 强 化 学 习。

二、进 化 算 法 引 导 策 略 搜 索 的 强 化 学 习

进 化 算 法 的 本 质 是 对解 空 间 进 行 搜 索 从 而 得 到 近 似 的 最 优 解 ， 因 此 对 于 强 化 学 习 问 题 ， 可 以 将 智 能 体 的 策 略看 作 解 空 间 ， 并 将 最 优 策 略 看 作 最 优解 ， 之 后 采 取类 似 进 化 算 法 的 搜 索 方 法 进 行 策 略 搜 索

1.参 数 分 布 搜 索 方 法

策 略 梯 度 方 法 的 思 想 是 增 加 累 计 奖 励 较 高 的 策 略 所 出 现 的 概 率 ， 这 与 进 化 策 略 的 思 想 类 似 ． 我 们 可 以 将 策 略看 作 一 个 分 布 ， 通 过 将 累 积 奖 励 作 为 适 应 度 函 数 ， 对策 略 的 参 数 空 间 进 行 搜 索 ，从  而 获 得 更 优 的 策 略

2.策 略 梯 度 近 似 方 法

可 以 看 作 使 用 进 化 算 法 进 行 参 数 搜 索 方 法 的 进 一 步 延 伸 ， 其利 用 强 化 学 习 的 思 想 ， 并 使 用 进 化 算 法 得 到 的 适 应 度 对 策 略 梯 度 进 行 近 似。

3.策 略 种 群 搜 索 方 法

与 参 数 分 布 搜 索 方 法 不 同 ， 策 略 种 群 搜 索 方 法 不 在 策 略 的 参 数 空 间 上 进 行 搜 索 ， 而 是 直 接 将 多 个 策 略 看 作 一 个 种 群 在 策 略 空 间 上 进 行 搜 索 ， 使 用 适 应 度 函 数 评 估 并 选 择 出 最 好 的 策 略 ． 这 类 方 法 将 强 化 学 习 与 进 化 算 法 通 过耦 合 度 较 低 的 方 式 结 合 起 来 ， 不 仅 可 以 在 具有 不 同 策 略 的 种 群 中 选 择 出 具 有 更 好 策 略 的 个 体 ， 同 时 还 可 以 用 于 在 具 有 不 同 超 参 数 的 策 略 的 种 群 中 进 行 超 参 数 的 搜 索。

三、进 化 算 法 经 验 指 导 的 深 度 强 化 学 习

进 化算法所具有 的 探索 能 力 是探 度 强 化 学 一直 以 来 所 缺 乏的 ，进 化 算法经验 指 导 的 深度强 化 学 习 指 的 是将进 化 算法 中 的 种 群 个体与环境交互 的 经验存 储 到 强 化学习 的 经 验 池 中 并 供其使用 的 一 类方法。分为：

1.无 反 馈 的 指 导

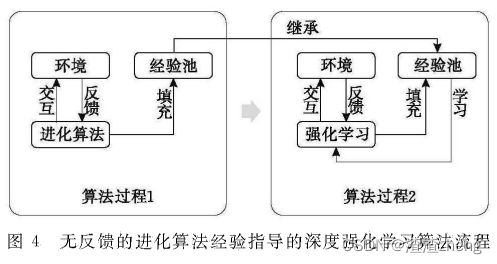
做 法 是 首 先 单独 使 用 进 化 算法先对环 境 进行搜索 ， 并 将 探 索 到 的 经验 存储下来 ， 之 后对这些 经 验 进 行 处 理 和 特 征 提取或直 接 作 为 深度强 化学 习 的 经验 ， 最 后再使用探 度强 化 学习 方 法对这 些 特 征 或 经 验 和 自 身 与 环境交互得到 的 经 验 一 并进 行利 用与 学习。

 

2.有 反 馈 的 指 导

无反馈 的 进 化算法 经 验 指导的 深度 强 化 学 习 将 进 化 算法 与 深度强化学习 过 程 进 行 了 分 离 ， 两 者 进 行 了 几 乎完全 的 解耦 ， 只通过经验池 进行联 系 ， 且两 个算法过程具 有 先 后 顺 序。有 反 馈 的 进 化 算法经 验指 导的 深 度强 化 学习 使 用了 经验 池 与 梯度 将 两 个 算法进行关联 ， 其中 梯 度 作 为 深度强化学习 给 进 化 算法 提 供 的 反 馈信息。 同 时 因 为 引 入 了 梯度作 用 ， 两 个算法 过程需要交替或并行运 行 。

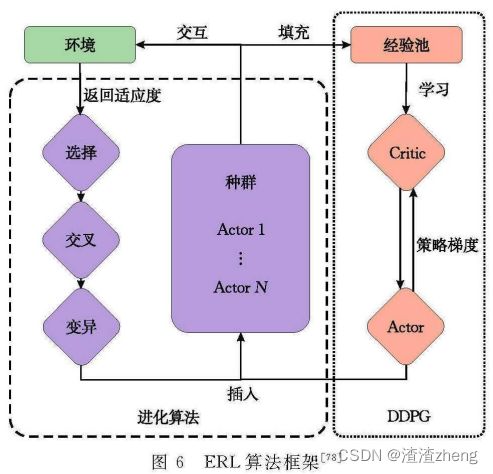
 Ｋｌｉａｄｋａ等 人  提 出 了 一 种 使 用 进 化算法经 验 指 导深度 强 化学习 的 框 架 ＥＲＬ ， 这是首次 将 迸 化算法 的 经验作 为 深度 强 化学习 的 指 导 且 同 时 将深度强化学 习 的 梯 度 信息 引入 进 化 算 法 的 一 种 方 法。

3.进 化 算 法 模块嵌入 的 深 度 强 化 学 习

 是 通 过 进 化 算 法解 决 深度 强 化 学 习 中 某 一 子 过 程 的 问 题 ， 使 得 进 化 算 法 作 为 一 个 关 键 的 组 件 嵌 入 并 参 与 到 深 度 强 化 学 习 的 过程 中 从 而 提 升 深 度 强 化 学 习 方 法 的 表 现 ， 其 主 要 特 点 是 一 般 不 能 再 以 回 合 为 单 位 来 进 行 种 群 的 评 估 ， 同 时 也 不 能 直 接 使 用 累 计 回 报 作 为 进 化 算 法 的 适 应 度 函 数 ， 其 适 应 度 函 数 需 要 进 行 特 定 的 设计。

四、总 结 与 展 望

（ １ ） 进 化 算 法 引 导 策 略 搜 索 的 强 化 学 习 中 的 参 数 搜 索 方 法 由 于 没 有 引 入 深 度 神 经 网 络 ， 因 此 解 决 问 题 的 能力 较 为 低 下 ． 尽 管 如 此 ， 这 类 方 法 充 分 地 利 用 了 进 化算 法 的 探 索 能 力 ， 将进 化算 法 直 接 用 于 参 数 空 间 的 探 索 这 一 思 想 与 之 后 将 进 化 算 法 用 于 深 度 强 化学 习 中 的 神 经 网 络 的 参 数探 索 的 思 想 是 一 致 的。

（2）进化算法与 其 它 基 于 梯 度 的 方 法 相 比 其 主 要 优 势 在 于 更 为 容 易 进 行 并 行 计 算 ， 从 而 大 幅 度 减 少 时 间 开 销 ． 未 来 可 以 致 力 于 让 此 类 方 法 解 决 更 高 维 度 的 问 题 ， 同 时 可 以 将 强 化 学 习 中 的 搜 索 与 探 索 方 式 引 人 其 中.

（3）与 深 度 强 化 学 习 相 结 合 的 方 法 大 多 数 采 用 了 基 于 actor-critic 的 策 略 梯 度 ， 这 是 目 前 深 度 强 化 学 习 领 域 中 最 为 成 熟 的 算 法 框 架 之一 。这 也 使 得 其 能 解 决 大 部 分 高 维 离 散 或 者 连 续 动 作 域 的 问 题 ． 对 于 这类 方 法 的 更 深 人 的 研究 ， 可 以 从 以 下 几个 方 向 着 手 进 行

① 进 化 算 法 普 遍 存 在 着 样 本 效 率 低 下 的 问 题 ， 虽 然 其 探 索 度 较 高 ， 但 其本 质 为 全 局 随 机 性 搜 索 ， 需 要 在 整 个 回 合 结 束 后 才 能 更 新 其 种 群 ， 而 深 度 强 化学 习 在 每个 回 合 步 中 都 会 得 到 大量 的 信 息 并 使 用 这 些 信 息 进 行 梯 度 更 新 ， 因 此 进 化 算 法 相 较 于 深 度 强 化 学 习 来 说 样 本 效 率 较 低 ． 针 对 进 化 算 法 样 本 效 率 的 问 题 ， 可 以 使 用 深 度 强 化 学 习 中 的 梯 度 和 回 合 步 中 的 其 它 信 息 对 其 进 行 指 导 ， 指 引 进 化 算 法 种 群 在 解 空 间 中 的 位 置 与 下 一 代 进 化 的 方 向 ．

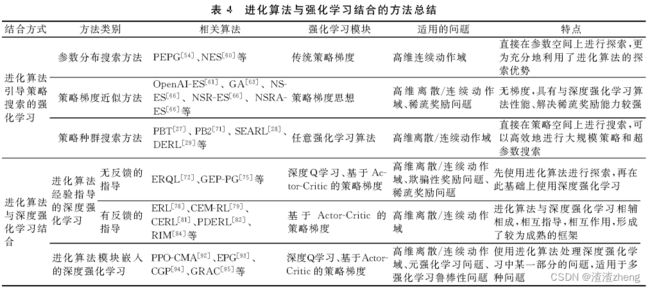
② 进 化算 法 与 深 度 强 化 学 习 的 兼 容 性 较 差 ， 从 表 ４ 中 可 以 看 出 目 前 进 化算 法 与 深 度 强 化 学 习 的 组 合 与 耦 合 方 式 较 为 单 一 ， 本 文 认 为 可 以 从 探 索 和 利 用 的 角 度 进 一 步 的 分 析 和 探 究 两 者 的 其 它 结 合 方 式 ． 平 衡 强 化 学 习 中 的 探 索 和 利 用 一 直 是 强 化 学 习 领 域 中 的 一 个 重 要 问 题 ， 在 与 进 化 算 法 结 合 的 深 度 强 化 学 习 中 也 需 要 对 两 者 进 行 更 为 合 理 的 平 衡 ， 如 引 入 新 颖度 与 探 索 度 等 一 些 度 量 方 式 在 进 化 算 法 的 探 索 和 深度 强 化 学 习 的 利 用 中 自 动 调 节 也 是 未 来 的 方 向 之 一 ．

③ 目 前结 合 进 化 算 法 与 深 度 强 化 学 习 的 方 法 中 均 与 最 新 的 同 类 方 法 进 行 了 比 较 ， 但 很 少 有 进 行 消 融 实 验 并 进 行 进 一 步 分 析 其 算 法 获 得 提 升 的 工 作 ． 进 化 算 法 本 身 为 一 种 启 发 式算 法 ， 其理 论 基 础 较 为 薄 弱 ， 且 与 深 度 强 化 学 习 一 样 均 不 能 保 证 其 收 敛 性 ， 因 此 本 文 认 为 需 要 加 强 对 算 法 性 能 提 升 的 分 析 与 实 验 ， 从 而 为 进 一 步 的 研究 打 下 基 础 ．

目 前 使用 进 化 算 法 与 深 度 强 化 学 习 结 合 的 方 法 还 较 少 ， 将 进 化 计 算 领 域 与 深 度 强 化 学 习 领 域 中 最 新 的 研究 成 果 应 用 于结 合 进 化 算 法 的 强 化 学 习 方 法 之 中 还 有 较 大 的 空 间 可 以 发 掘。

参考

吕帅,龚晓宇,张正昊,韩帅,张峻伟.结合进化算法的深度强化学习方法研究综述[J].计算机学报,2022,45(07):1478-1499.