马尔科夫链(Markov Chain)
1,马尔可夫性
马尔可夫性(Markov Property)是指系统的下一个状态![]() 仅与当前状态
仅与当前状态![]() 有关,而与以前的状态无关
有关,而与以前的状态无关
(即无记忆性(memorylessness),系统不记得当前状态以前的状态,仅仅基于当前状态来决定下一个时刻转移到什么状态)
2.马尔科夫链
如果指标集(index set)是连续的,则称为连续时间马尔可夫链(Continuous-Time MC, CTMC)
如果指标集是离散的,则称为离散时间马尔可夫链(Discrete-Time MC, DTMC)
![]()
1,某一时刻状态转移的概率只依赖于它的前一个状态( Xn+1 的概率只和之前的 Xn 的概率有关,称为无记忆性)==求出系统中任意两个状态之间的转换概率,就能确定马尔科夫链模型
2,状态的改变叫做转移,不同的状态改变的概率叫做转移概率==转移概率矩阵
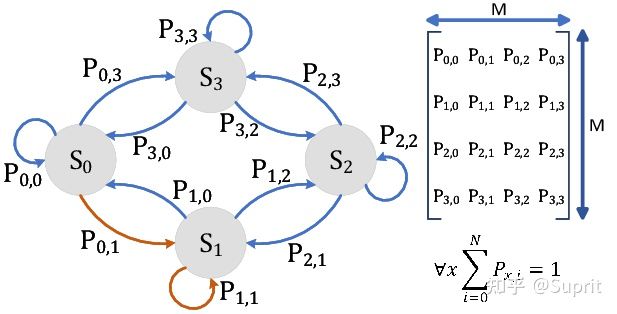
转移矩阵(状态转移矩阵)
(矩阵相乘)
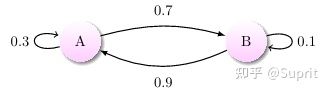
马尔科夫链的状态转移也可以用一个有向图(directed graph)来表示。其中的节点表示状态,边(edge)的箭头方向表示状态转移的方向,而edge上的数值则表示对应状态转移的概率
举例1
有 A 和 B 两个状态,A 到 A 的概率是 0.3,A 到 B 的概率是 0.7;B 到 B 的概率是 0.1,B 到 A 的概率是 0.9
转移概率矩阵
复杂情况例子2
简述马尔可夫链【通俗易懂】 - 知乎 (zhihu.com)
主要特征:
1,状态空间可以是任何东西:字母,数字,篮球比分或者天气情况转移矩阵
2,转移矩阵:描述了特定转移发生的概率
3,初始状态:由初始分布给出的状态空间的初始状态
状态转移矩阵的稳定性
经过一定有限次数序列的转换,最终一定可以得到一个稳定的概率分布 ,且与初始状态无关
实现
用 Python 实现马尔可夫链
初始状态为
#导入库
import numpy as np
#设定转移矩阵
matrix = np.matrix([[0.3, 0.7],
[0.9, 0.1]])
#初始状态为[1,0]
vector1 = np.matrix([[1, 0]])
for i in range(50):
vector1 = vector1 * matrix
print('第{}轮'.format(i + 1))
print(vector1)第36轮开始,状态概率分布就不变了,一直保持在[0.5625 0.4375],并且改变初始状态,第37轮开始保持在[0.5625 0.4375],采用了不同初始概率分布,最终状态的概率分布趋于同一个稳定的概率分布即状态转移矩阵的稳定性
来源MCMC(二)马尔科夫链 - 刘建平Pinard - 博客园 (cnblogs.com)
3,马尔可夫模型建模步骤
1,分级或分类——相互独立
分级:样本均值——标准差分级法、逐步聚类法、模糊聚类法
分类:根据变量地区、变量属性
2,检验马尔可夫性——马氏检验、卡方检验
3,计算马尔可夫转移矩阵(多步或者每一步取平均)
4,预测
案例
MCMC(二)马尔科夫链 - 刘建平Pinard - 博客园
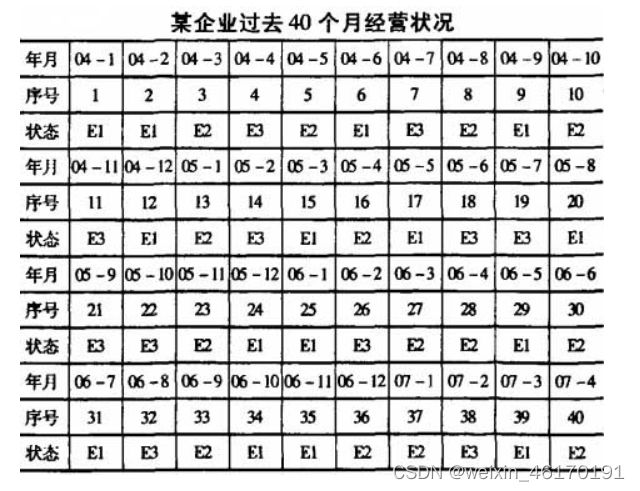
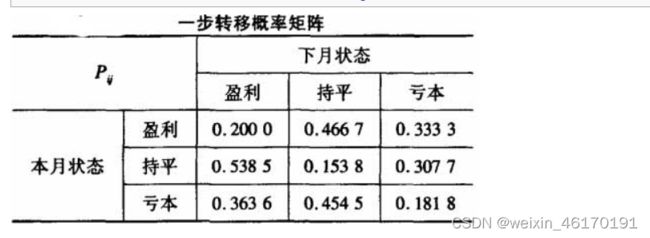
1,分级或分类:假设某企业的经营状况分为盈利、持平、亏本3种状态,分别记为E1、E2、E3
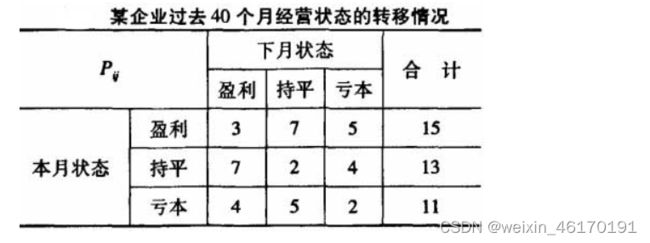
3,计算马尔可夫转移矩阵(多步或者每一步取平均)
15个从El出发的状态中,有3个转移到了El,7个转移到了E2,5个转移到了E3。
相应得出从E2和E3出发的状态的转移情况。
从盈利到盈利的一步转移概率:
从持平到亏本的一步转移概率:
参考:
简述马尔可夫链【通俗易懂】 - 知乎 (zhihu.com)
什么是马尔可夫链? - 知乎 (zhihu.com)
MCMC(二)马尔科夫链 - 刘建平Pinard - 博客园 (cnblogs.com)