GNN for NLP综述

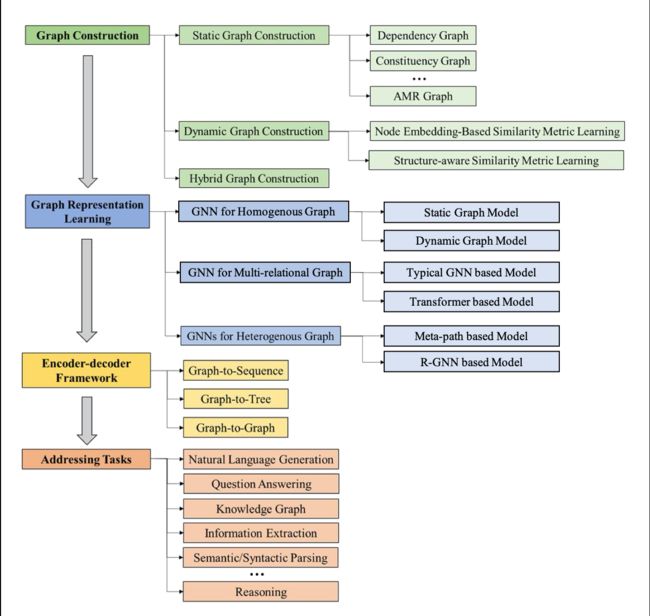
图1：分类法，它沿着四个轴系统地组织NLP的GNN：图构建、图表示学习、编码器-解码器模型和applications。

摘要

深度学习已经成为处理自然语言处理（NLP）中各种任务的主要方法。尽管文本输入通常表示为一系列标记，但有大量的NLP问题可以用图结构最好地表达。因此，为大量NLP任务开发新的图深度学习技术的兴趣激增。在这项调查中，我们对用于NLP的图神经网络（GNN）进行了全面综述。我们提出了一种新的NLP GNN分类法，它沿着三个轴系统地组织了NLP GNNs的现有研究：图构建、图表示学习和基于图的编码器-解码器模型。我们进一步介绍了大量利用GNN功能的NLP应用程序，并总结了相应的基准数据集、评估指标和开源代码。最后，我们讨论了在NLP中充分使用GNN的各种突出挑战以及未来的研究方向。据我们所知，这是用于NLP的GNN的第一个全面概述。

1. 引言

深度学习已成为当今NLP中处理各种任务的主要方法，尤其是在大规模文本语料库上操作时。传统上，在NLP任务中，文本序列被视为a bag of token，例如BoW和TF-IDF。随着最近单词嵌入技术的成功（Mikolov, 2013；Pennington, 2014），在NLP任务中，句子通常被表示为a sequence of token。因此深度学习技术，如递归神经网络（Schuster和Paliwal, 1997）和卷积神经网络（Krizhevsky, 2012）已广泛应用于文本序列建模。
然而，有大量的NLP问题可以用图结构来表达。例如：

• 文本序列中的句子结构信息（即句法分析树，如依存关系和选区分析树）
  • 作用：被利用来通过结合任务特定知识来扩充原始序列数据。
• 序列数据中的语义信息（即语义解析图，如抽象意义表示图和信息提取图）
  • 作用：用于增强原始序列数据。

因此，这些图结构数据可以编码实体token之间的复杂成对关系，以学习更多信息表示。

图深度学习领域的发展，和NLP交叉点的研究影响了多种NLP任务（Liu和Wu, 2022）。人们对应用和开发不同的GNN变体的兴趣激增，并在许多NLP任务中取得了相当大的成功。包括：

• 分类任务，如句子分类（Henaff, 2015；Huang和Carley，2019）、语义角色标记（Luo和Zhao，2020；Gui, 2019）和关系提取（Qu, 2020；Sahu, 2019年）
• 生成任务，如机器翻译（Bastings, 2017年；Beck, 2018a）、问题生成（Pan, 2020年；Sachan, 2020）和摘要（Fernandes, 2019年；Yasunaga, 2017）。

尽管这些现有研究已经取得了成功，但NLP图的深度学习仍然面临许多挑战

• 自动将原始文本序列数据转换为高度图结构的数据。
• 正确确定图表示学习技术。
• 有效地建模复杂数据。

在此综述中，我们将首次全面概述用于NLP的GNN。此综述对机器学习和NLP社区都是及时的，涵盖了相关和有趣的主题，包括NLP的自动图构建、NLP的图表示学习、NLP中基于GNN的各种高级encoder-decoder模型（即graph2seq、graph2tree和graph2graph），以及GNN在各种NLP任务中的应用。我们的主要贡献如下：

• 提出了一种新的NLP GNN分类法，它沿着四个轴系统地组织了NLP GNNs的现有研究：图构建、图表示学习和基于图的编码器-解码器模型。
• 对各种NLP任务的最先进的基于GNN的方法进行了最全面的概述。提供了基于领域知识和语义空间的各种图构建方法的详细描述和必要的比较，针对各种类型的图结构数据的图表示学习方法，给定输入和输出数据类型的不同组合的基于GNN的encoder-decoder模型。
• 引入了大量利用GNN功能的NLP应用程序，包括它们如何沿着三个关键组件（即图构建、图表示学习和嵌入初始化）处理这些NLP任务，以及提供相应的基准数据集、评估指标和开源代码。
• 概述了在NLP中充分利用GNN的各种突出挑战，并为富有成效和未探索的研究方向提供了讨论和建议。

2. Graph Based Algorithms for NLP

图的角度回顾了NLP问题，然后简要介绍了解决NLP问题的一些有代表性的传统基于图的方法。

2.1 NLP: A Graph Perspective

• 将自然语言示表为a bag of tokens.
• 将自然语言表示为a sequence of tokens。
• 将自然语言表示为图。图在NLP中无处不在。虽然将文本视为顺序数据可能是最明显的，但在NLP中，将文本表示为各种图的历史由来已久。文本或世界知识的常见图表示包括依赖关系图、选区图、AMR图、IE图、词汇网络和知识图。此外，还可以构建包含文档、段落、句子和单词等元素的多层次结构的文本图。与上述两种观点相比，这种自然语言的观点能够捕捉文本元素之间更丰富的关系。正如下一节中介绍的，许多传统的基于图的方法（例如，随机游走、标签传播）已经成功地应用于具有挑战性的NLP问题，包括词义消歧、名称消歧、共指解析、情感分析和文本聚类。

2.2 Graph Based Methods for NLP

2.2.1 随机游走的算法：

• 文本的语义相似性度量（Ramage, 2009）
• 语义网络上的语义距离度量（Hughes和Ramage，2007）
• 词义消歧（Mihalcea，2005；Tarau, 2005）
• 名称消歧（Minkov, 2006）
• 查询扩展（Collins Thompson和Callan，2005）
• 关键词提取（Mihalcea和Tarau，2004）
• 跨语言信息检索（Monz和Dorr，2005）

2.2.2 图聚类算法

常见的图聚类算法包括谱聚类、随机游走聚类和最小截聚类。

2.2.3 图匹配算法

图匹配算法旨在计算两个图之间的相似度。

2.2.4 标签传播算法

标签传播算法（Label propagation algorithms LPAs）是一类基于半监督图的算法，它将标签从标记的数据点传播到先前未标记的数据。

• 词义消歧（Niu, 2005）
• 情感分析（Goldberg和Zhu，2006）

2.2.5 GNNs的局限性和联系

传统的基于图的算法有几个局限性。

• 表达能力有限。它们主要集中于捕获图的结构信息，但不考虑节点和边特征
• 没有统一的学习框架。不同的基于图的算法具有非常不同的属性和设置，并且仅适用于某些特定的用例

GNN可以对任意的图结构数据进行建模。大多数GNN变体可以被视为基于消息传递的学习框架。与传统的基于消息传递的算法（如LPA）不同，GNN通过在图上传播标签来操作，GNN通常通过几个神经层来转换、传播和聚集节点/边特征，以便学习更好的图表示。作为一个通用的基于图的学习框架，GNN可以应用于各种与图相关的任务，如节点分类、链接预测和图分类。

3. Graph Neural Networks

本章阐述GNN的基本基础和方法，这是一类直接对图结构化数据进行操作的现代NN（Wu, 2022）

3.1 Foundations

GNN本质上是图表示学习模型，可以应用于节点级别的任务和图级别的任务。GNN为图中的每个节点学习嵌入，并将节点嵌入聚集起来产生图的嵌入。一般来说，节点嵌入的学习过程利用了输入的节点嵌入和图结构，可以总结为：
${\mathbf{h}}_i^{(l)}=f_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}}(\mathbf{A},{\mathbf{H}}^{(l-1)})$
即输入邻居节点矩阵$\mathbf{A}\in {\mathbb{R}}^{n\times n}$和上一层的节点表示${\mathbf{H}}^{l-1}=\{{\mathbf{h}}_1^{l-1},{\mathbf{h}}_2^{l-1},\cdots ,{\mathbf{h}}_n^{l-1}\}$，可以更新得到下一层的节点表示，不同的模型在于图滤波器的选择和参数。
由于图过滤不会改变图结构，因此在聚合节点嵌入时引入了池化操作，以生成图级别的嵌入。在GNN模型中，图池化将图及其节点嵌入作为输入，然后生成具有较少节点的较小图及其相应的新节点嵌入。图池化操作可总结如下：
$\mathbf{A},{\mathbf{H}}^{\prime }=f_{\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}}(\mathbf{A},\mathbf{H})$

3.2 方法

3.2.1 图滤波器

图滤波器存在多种实现方式，大致可分为基于谱域的图滤波器、基于空间域的图滤波器、基于注意力的图滤波器和基于递归的图滤波器。从概念上讲，基于谱域的图滤波器是基于谱图理论的，而基于空域的方法则是利用图空间上的邻居节点来计算节点嵌入。一些基于谱域的图滤波器可以被转换为基于空间的图滤波。基于注意力的图滤波器受到自注意力机制的启发，对不同的邻居节点分配不同的注意力权重。基于递归的图滤波器引入了门控机制，模型参数在不同的GNN层之间共享。

• **基于谱域的图滤波器：**图上的谱卷积定义为信号$x_i$（节点$v_i$的标量）与傅里叶域中$\theta$参数化的滤波器$f_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}}$的乘积：

$f_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}}\ast {\mathbf{x}}_i=\mathbf{U}f(\mathbf{\Lambda }){\mathbf{U}}^T{\mathbf{x}}_i$
其中$\mathbf{U}$是归一化图拉普拉斯$\mathbf{L}={\mathbf{I}}_n-{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}$的特征向量矩阵

• 基于空间域的图滤波器
  • MPNN：${\mathbf{h}}_i^{(l)}=f_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}}(\mathbf{A},{\mathbf{H}}^{(l-1)})=f_U({\mathbf{h}}_i^{(l-1)},{\sum }_{v_j\in \mathcal{N}(v_i)}{f}_M({\mathbf{h}}_i^{(l-1)},{\mathbf{h}}_j^{(l-1)},{\mathbf{e}}_{i,j})$
  • GraphSAGE：$f_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}}(\mathbf{A},{\mathbf{H}}^{(l-1)})=\sigma ({\mathbf{W}}^{(l)}\cdot f_M({\mathbf{h}}_i^{(l-1)},\{{\mathbf{h}}_j^{(l-1)},\mathcal{N}(v_i)\}))$
• 基于注意力的图滤波器

${\alpha }_{ij}=\frac{\exp \left(\mathrm{LeakyReLU}\left(u^{(l)T}\left[W^{(l)}{\mathbf{h}}_i^{(l-1)}\Vert W^{(l)}{\mathbf{h}}_j^{(l-1)}\right]\right)\right)}{{\sum }_{v_k\in N\left(v_i\right)}\exp \left(\mathrm{LeakyReLU}\left(u^{(l)T}\left[W^{(l)}{\mathbf{h}}_i^{(l-1)}\Vert W^{(l)}{\mathbf{h}}_k^{(l-1)}\right]\right)\right)}$

• **基于递归的图滤波器：**门控图神经网络（GGNN）滤波器

$\begin{array}{rl}{\mathbf{h}}_i^{(0)}& ={\left[{\mathbf{x}}_i^T,0\right]}^T\\ {\mathbf{a}}_i^{(l)}& =A_{i:}^T{\left[{\mathbf{h}}_1^{(l-1)}\dots {\mathbf{h}}_n^{(l-1)}\right]}^T\\ {\mathbf{h}}_i^{(l)}& =\mathrm{GRU}\left({\mathbf{a}}_i^{(l)},{\mathbf{h}}_i^{(l-1)}\right)\end{array}$

3.2.2 图池化

图池化层用于以图为重点的下游任务生成图级表示，如基于学习到的节点嵌入进行图分类和预测。图级别的任务来说，需要整个图的表示。为此，需要对节点嵌入信息和图结构信息进行总结。图池化层可以分为两类：flat图池化和分层图池化。

• flat图池化：单个步骤中直接从节点嵌入中生成图级别表示。
• 分层图池化：包含几个图池化层。

4. 用于NLP任务的图构建方法

对于大多数NLP任务来说，典型的输入是文本序列而非图。为了利用GNN，如何从文本序列中构建一个图输入成为一个艰难的步骤。在本章重点介绍两种主要的图构建方法，即静态图构建（Dependency Graph Construction，Constituency Graph Construction，AMR Graph Construction，Discourse Graph Construction，information extraction graph，Discourse Graph Construction，Knowledge Graph Construction，Knowledge Graph Construction，Similarity Graph Construction，Co-occurrence Graph Construction。Topic Graph Construction，App-driven Graph Construction）和动态图构建，此外介绍了多种图相似度度量准则，用于构建各种NLP任务中的图结构输入。

4.1 静态图构建

静态图构建方法是在预处理期间构建图结构，通常是利用现有的关系解析工具（如依存分析）或手动定义的规则。从概念上讲，静态图包含了隐藏在原始文本序列中的不同领域/外部知识，从而用丰富的结构化信息来扩充原始文本。

4.1.1 静态图构建方法

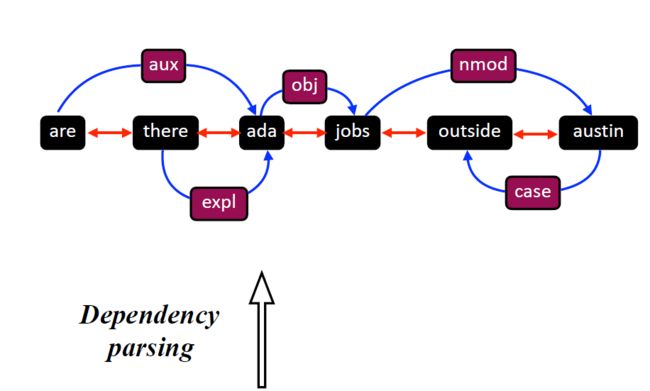
1.依赖图构建（Dependency Graph Construction）

• 依赖图被广泛用于捕捉给定句子中不同对象之间的依赖关系。形式上，给定一个段落，
  • 1). 通过使用各种NLP解析工具（例如Stanford CoreNLP）获得依赖解析树（例如句法依赖树或语义依赖解析树）。
  • 2). 从依赖解析树中提取依赖关系，并将其转换为依赖图。由于给定段落有顺序信息，而图的节点是无序的，可以引入顺序的link，在图结构中保留这种重要信息。
• 给定输入段和其提取的分析树，包括三个关键步骤。1）构建依赖关系，2）构建顺序关系，3）最终的图转换。

2.选区图构建（Constituency Graph Construction）

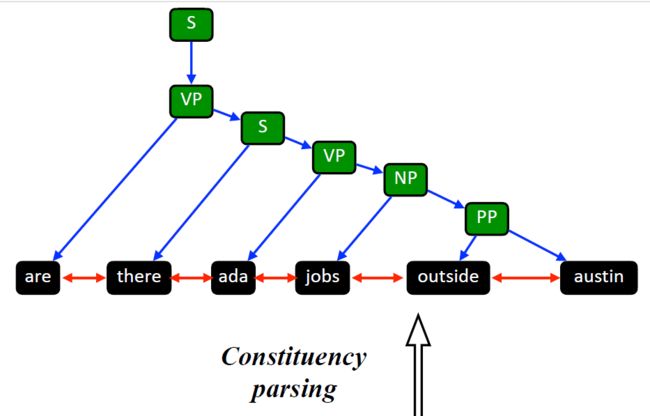
• 选区图能够捕捉一个或多个句子中基于短语的句法关系。与依赖分析不同的是，依赖分析只关注单个词之间一对一的对应关系（即词级），选取分析建模一个或几个对应词的组合（即短语级）
• Step 1：选区关系。在语言学中，选区关系是指遵循短语结构语法的关系，而不是依赖关系和依赖语法。**通常选区关系源自主语（名词短语NP）-谓语（动词短语VP）关系。**在这一部分只讨论从选区解析树导出的选区关系。与所有节点都具有相同类型的依赖关系解析树不同，选区解析树区分终端节点和非终端节点。选区语法的非终端类别标记解析树的内部节点（例如，S代表句子，NP代表名词短语）
• Step 2：选区图。选区图$\mathcal{G}(\mathcal{V},\mathcal{E})$由非终端节点${\mathcal{V}}_{nt}$，终端节点${\mathcal{V}}_{word}$，选区边以及顺序边组成。类似于依赖图，给定段落段落和选区关系集${\mathcal{R}}_{cons}$，针对每个选区关系$(w_i,re{l}_{i,j},w_j)\in {\mathcal{R}}_{cons}$，添加节点$v_i$（单词$w_i$），节点$v_j$（单词$w_j$）以及从$v_i$到$v_j$的有向边。然后，对于原始文本中相邻单词的每个单词节点对$(v_i,v_j)$，在它们之间添加具有特定顺序类型的无向边。这些顺序边用于保留顺序信息。

3.抽象语义表示图构建（AMR Graph Construction）

图3 AMR Graph
AMR图是有根节点、标签、有向、无环的图，它被广泛用于表示非结构化和具体自然文本的抽象概念之间的高级语义关系。与句法上的特异性不同，AMR是高级语义抽象。更具体地，语义上相似的不同句子可能共享相同的AMR解析结果。AMR图是由AMR解析树衍生出来的。
4.信息抽取图构建（Information Extraction Graph Construction）

图4 Information Extraction Graph

• 信息抽取图（IE Graph）目的是提取结构信息来表示自然句子（例如基于文本的文档）之间的高级信息。这些提取出来的关系，捕捉远距离句子之间的关系。为给定段落构建IE图的过程分为三个基本步骤。
  • 1）指代消解
  • 2）构建IE关系
  • 3）图的构建。

5.话语图构建（Discourse Graph Construction）

• 当候选文档太长时，许多NLP任务会受到长依赖性的挑战。话语图描述了两个句子之间的逻辑联系，可以有效地解决这种挑战。

6.知识图构建（Knowledge Graph Construction）

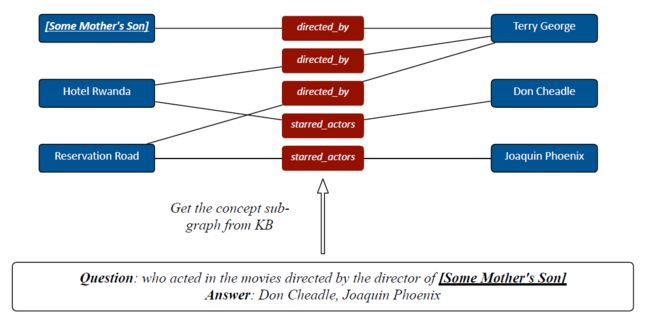
图5 knowledge graph

• 捕捉实体和关系的知识图（KG）可以极大地促进许多NLP应用中的学习和推理。KG可以表示为$\mathcal{G}(\mathcal{V},\mathcal{E})$，通常由知识库中的元素构建。形式上，定义三元组$(e_1,rel,e_2)$作为知识库的基本元素，$e_1$是源实体，$e_2$是目标实体和$rel$是关系类型。然后在知识库中添加两个节点，即源节点$v_1$和目标节点$v_2$，并从$v_1$到$v_2$添加一条边类型为$rel$的有向边。

7.共指图构建（Coreference Graph Construction）

• 在语言学中，当给定段落中的两个或多个术语引用同一个对象时，会出现共指。共指现象有助于更好地理解语料库的复杂结构和逻辑，并解决歧义。为了有效地利用共指信息，共指图用来显式的建模隐性共指关系。给定一组短语，共指图可以连接文本语料库中指代同一实体的节点（短语）。

8.相似图构建（Similarity Graph Construction）

图6 similarity graph

• 相似性图旨在量化节点之间的相似性。由于相似度图通常是面向应用的，因此专注于为各种类型的元素（如实体、句子和文档）构建相似度图的基本过程，而忽略了特定于应用的细节。相似度图的构建是在预处理期间进行的，并且没有以端到端的方式与剩余的学习系统联合训练。相似图的一个示例如图6所示。

9.共现图构建（Co-occurrence Graph Construction）

图7 co-occurrence graph

• 共现图旨在捕捉文本中单词之间的共现关系，这在许多NLP任务中被广泛使用，共现关系描述了在固定大小的上下文窗口内共同出现的两个词的频率，是捕捉语料库中词之间语义关系的一个重要特征。共现图的例子见图7。

10.话题图构建（Topic Graph Construction）

图8 topic graph

• 话题图是建立在几个文档上的，目的是对不同主题间的高层次语义关系进行建模。给定一组文档，首先用一些话题建模算法，如LDA学习潜在的话题。然后构建话题图，只有当文档具有该话题时，那么在文档节点和话题节点之间构建一条无向边。

11.应用驱动图构建（App-driven Graph Construction）

图9 application-driven graph

• 应用驱动图指的是为特定的NLP任务专门设计的图。在一些NLP任务中，使用特定应用的方法通过结构化的形成来表示非结构化的数据很常见。例如，SQL语言可以自然地通过SQL解析树来表示，因此可以被转换为SQL图。由于这类图基于领域知识过于专业化，因此没有统一的模式来总结如何建立一个应用驱动的图。图9是这种应用驱动图的一个例子。

4.1.2 混合图构建和讨论

以前的大多数静态图构建方法只考虑节点之间的一种特定关系。尽管所获得的图在某种程度上很好地捕捉了结构信息，但它们在利用不同类型的图关系方面也受到限制。为了解决这一限制，越来越关注通过将多个图组合在一起构建混合图，以丰富图中的语义信息。

4.2 动态图构建

尽管静态图的构建具有将数据的先验知识编码到图结构中的优势，但它有几个局限性：

• 1）为了构建一个性能合理的拓扑结构，需要大量的人力和领域知识；
• 2）人工构建的图结构可能容易出错（例如，有噪声或不完整）；
• 3）由于图构建阶段和图表示学习阶段是不相干的，在图构建阶段引入的错误不能被纠正，可能会累积到后面的阶段，这可能导致性能下降；
• 4）图的构建过程往往只由机器学习从业者的见解来决定，对于下游的预测任务来说可能是次优的。

为了应对上述挑战，最近关于NLP的GNN开始探索动态图的构建，而不需要借助人工或领域专业知识。大多数动态图构建方法旨在动态学习图结构（即加权邻接矩阵），图构建模块可以与后续的图表示学习模块共同优化，以端到端的方式面向下游任务。如图10所示，这些动态图构建方法通常包括一个图相似性度量学习组件，用于通过考虑嵌入空间中的成对节点相似性来学习邻接矩阵，以及一个图稀疏化组件，用于从学到的全连接图中提取稀疏图。将内在图结构和学习的隐含图结构结合起来，有利于提高学习性能。此外，为了有效地进行图结构和表征的联合学习，人们提出了各种学习范式。GNN的图结构学习本身就是机器学习领域的一个趋势性研究问题，并且已经在NLP之外被广泛研究然而，在本综述将重点介绍其在NLP领域的最新进展，将动态图构建和图结构学习交替使用。

图10 dynamic graph construction

4.2.1 图相似度度量技术

基于节点属性包含学习隐式图结构的有用信息的假设，最近有工作将图结构学习问题转化为定义在节点嵌入空间的相似度量学习问题。学习到的相似性度量函数以后可以应用于未见过的节点嵌入集来推断图结构，从而实现归纳式图结构学习。对于部署在非欧几里得领域（如图）的数据，欧几里得距离不一定是衡量节点相似性的最佳指标。各种相似性度量函数已用于GNN的图结构学习。根据所利用的信息源的类型，将这些度量函数分为两类：基于节点嵌入的相似性度量学习和结构感知的相似性度量学习。

• 基于节点嵌入的相似度度量学习：基于节点嵌入的相似性度量函数被设计为通过计算嵌入空间中的成对节点相似性来学习加权邻接矩阵。
  • 基于注意力机制的相似度度量函数
    • 为了提高基于点积的注意力机制的学习能力，Chen等人通过引入可学习的参数，提出了一个改良的点积，表述如下：

$S_{i,j}=({\mathbf{v}}_i\odot \mathbf{u}{)}^T{\mathbf{v}}_j$
其中$\mathbf{u}$是一个非负的权重向量，用于提升节点嵌入不同维度的影响力。

  - Chen等人通过引入一个可学习的权重矩阵设计了一个更具有表达能力的点积方式：

$S_{i,j}=ReLU(\mathbf{W}{\mathbf{v}}_i{)}^{T}ReLU(\mathbf{W}{\mathbf{v}}_j)$

• 基于Cosine相似度的度量函数
  • Chen等人（2020e）将香vanilla余弦相似性扩展为多头加权余弦相似性，以从多个角度捕捉成对节点的相似性：

$\begin{array}{rl}{S}_{i,j}^p& =\cos \left(w_p\odot v_i,w_p\odot v_j\right)\\ S_{i,j}& =\frac{1}{m}\sum _{p=1}^m{S}_{ij}^p\end{array}$

• 结构感知的相似度学习
  • 受结构感知 transformers 启发，一些方法采用了结构感知的相似性度量函数，在节点信息之外还额外考虑了内在图的现有边信息。例如，Liu等人(2019c)提出了一个学习成对节点相似性的结构感知注意机制，如下：

$S_{i,j}^l=\mathrm{softmax}\left(u^T\tanh \left(W\left[h_i^l,h_j^l,v_i,v_j,e_{i,j}\right]\right)\right)$

• $e_{i,j}$是边的嵌入表示。Liu et al. (2021b) 提出了结构感知的全局注意力机制：

$S_{i,j}=\frac{\mathrm{ReLU}{\left(W^Q{v}_i\right)}^T\left(\mathrm{ReLU}\left(W^K{v}_i\right)+\mathrm{ReLU}\left(W^R{e}_{i,j}\right)\right)}{\sqrt{d}}$

4.2.2 图稀疏化技术

现实场景中的大多数图都是稀疏的图。相似性度量函数考虑任何一对节点之间的关系，并返回一个完全连接的图，这不仅计算成本高，而且还可能引入噪音，如不重要的边。因此，对所学的图结构明确地强制执行稀疏性是有益的。除了在相似度量函数中应用ReLU函数，还采用了各种图稀疏化技术来提高所学图形结构的稀疏性。

• 应用kNN式的稀疏化操作，从相似度学习函数计算的节点相似度矩阵中获得稀疏的邻接矩阵

4.2.3 结intrinsic图结构和隐式图结构

最近的研究表明，如果在进行动态图构建时完全丢弃内在图结构，可能会损害下游任务的性能。这可能是因为intrinsic图通常仍然带有关于下游任务的最佳图结构的丰富和有用的信息。因此，他们提出将学习到的隐式图结构与intrinsic图结构结合起来，基于这样的假设：学习到的隐式图有可能是intrinsic图结构的 “转变”（例如，子结构），是对intrinsic图结构的补充。另一个潜在的好处是纳入intrinsic图结构可能有助于加速训练过程，提高训练的稳定性。

4.2.4 学习范式

大多数现有的GNN动态图构建方法包括两个关键的学习组件：图结构学习（即相似性度量学习）和图表示学习（即GNN模块），最终目标是学习与某些下游预测任务相关的优化图结构和表示。如何优化这两个独立的学习组件以达到相同的最终目标成为一个重要问题。这里我们强调三个有代表性的学习范式。

• 1）最直接的策略，端到端的方式联合优化整个学习系统，以实现下游（半）监督预测任务；
• 2）自适应学习每个堆叠GNN层的输入图结构以反映中间图表示的变化。这类似于transformer 如何在每一层学习不同的加权全连接图；
• 3）迭代式的图学习框架，即在更好的图表示的基础上学习更好的图结构，同时以迭代的方式学习更好的图表示。因此，这种迭代学习范式反复完善图结构和图表示，以达到最佳的下游性能。

5. Graph Representation Learning for NLP

图表示学习的目标是找到一种方法，通过机器学习模型将图的结构和属性信息结合到低维空间中。形式化这个问题：图表示为$\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{T},\mathcal{R})$,其中$\mathcal{V}$是节点集，$\mathcal{E}$是边集，$\mathcal{T}=\{T_1,T_2,\cdots ,T_p\}$是节点类型集合，$\mathcal{R}=\{R_1,R_2,\cdots ,R_q\}$是边类型集合。$|\cdot |$是元素的数量。$\tau (v_i)\in \mathcal{T}$表示节点$v_i$的类型。$\varphi (e_{i,j})\in \mathcal{R}$表示边$e_{i,j}$的类型
一般来说，从原始文本数据构建的图可能是同质图或异质图。第5.1节将讨论同质图的各种图表示学习方法，包括原始同质图和一些从异质图转换过来的方案。第5.2节将讨论基于GNN的作用于多关系图的方法，第5.3节讨论处理异质图的GNN。

5.1 GNNs for Homogeneous Graphs

根据定义，对于图$\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{T},\mathcal{R})$，当$|\mathcal{T}|=1,|\mathcal{R}|=1$被称为同质图。大多数GNN，如GCN、GAT和GraphSage，都是为同质图设计的，然而这并不能很好地适配许多NLP任务。例如，给定一个自然语言文本，构建的依赖图是包含多种关系的任意图，传统的GNN方法无法直接利用。本小节将首先讨论将任意图转换为同质图的各种策略，包括静态图和动态图。然后讨论考虑双向编码的GNN。

5.1.1 静态图

处理静态图的GNN通常包括两个阶段，即转换边信息和节点表示学习。

1. 将边信息转换为相邻矩阵

边被看作是节点之间的连接信息。在这种情况下，丢弃边类型信息并保留连接信息，将异质图转换成同质图。得到这样的图后，可以将图的拓扑结构表示为统一的邻接矩阵$\mathbf{A}$，对于边$A_{i,j}$表示加权静态图上的边权重，若$A_{i,j}=1$表示无权重,若$A_{i,j}=0$表示无连接。对于无向图邻接矩阵是对称矩阵，即$A_{i,j}=A_{j,i}$。对于有向图邻接矩阵是非对称矩阵，有向图可以通过平均两个方向的边权重转化为无向图。

2. 节点表示学习

给定初始节点嵌入$\mathbf{x}$和邻接矩阵$\mathbf{A}$，基于经典的GNNs技术提取节点表示。
对于无向图，大多数工作主要采用图表示学习算法，如GCN、GGNN、GAT、GraphSage等，并将它们堆叠起来探索图中的深层语义关联。
当涉及到有向图时，少数GNN方法如GGNN、GAT仍然有效。而对于其他不能直接应用于有向图的GNN，简单的策略是忽略方向（即把有向图转换为无向图）。然而，这种方法允许消息在两个方向上传播而不受约束。为了解决这个问题，很多工作来使GNN适应于有向图。对于GCN，一些基于空间的GCN算法是为有向图设计的，如DCNN。GraphSage通过修改聚合函数，通过指定边方向并分别聚合扩展到有向图上。

5.1.2 动态图

动态图旨在与下游任务共同学习图结构。早期的工作主要采用递归网络，将图节点嵌入作为RNN的状态编码，这可以看作是GGNN的雏形。然后，经典的GNN如GCN、GAT、GGNN 被用来有效地学习图嵌入。最近的研究者采用基于注意力或基于度量学习的机制，从非结构化文本中学习隐含的图结构。图结构的学习过程是通过端到端的方式与下游任务相结合。

5.1.3 双向图嵌入

本小节讨论了如何处理边方向。在现实中许多图都是有向无环图（DAG），其信息是沿着特定的边方向传播的。一些研究者允许信息在两个方向上平等传播，另一些研究者则抛弃了包含在边中的信息，这两种情况对于最终的表示学习会损失一些重要结构信息。为了解决这个问题，提出了双向图神经网络（bidirectional GNN），以交错的方式从传入和传出的边上学习节点表示。
对于图$\mathcal{G}(\mathcal{V}，\mathcal{E})$中节点$v_i\in \mathcal{V}$及其邻居节点$N(v_i)$，将传入（向后）节点集定义为满足$e_{j,i}\in \mathcal{E},v_j\in N_{⊣}\left(v_i\right)$的$N_{⊣}\left(v_i\right)$，而传出（向前）节点集为满足$e_{i,j}\in \mathcal{E},v_j\in N_{⊢}\left(v_i\right)$的$N_{⊢}\left(v_i\right)$。
Xu等人(2018b)首先将GraphSage扩展到双向版本，先分别计算每个方向的图嵌入，最后将其组合。在每个计算跳，对于图中的每个节点，它们分别聚合传入节点和传出节点，以获得向后和向前立即聚合表示，如下所示：
$\begin{array}{l}{\mathbf{h}}_{i,⊣}^{(k)}=\sigma \left({\mathbf{W}}^{(k)}\cdot f_k^{⊣}\left({\mathbf{h}}_{i,⊣}^{(k-1)},\left\{{\mathbf{h}}_{j,⊣}^{(k-1)},\forall v_j\in N_{⊣}\left(v_i\right)\right\}\right)\right)\\ {\mathbf{h}}_{i,⊢}^{(k)}=\sigma \left({\mathbf{W}}^{(k)}\cdot f_k^{⊢}\left({\mathbf{h}}_{i,⊢}^{(k-1)},\left\{{\mathbf{h}}_{j,⊢}^{(k-1)},\forall v_j\in N_{⊢}\left(v_i\right)\right\}\right)\right)\end{array}$
其中$k\in \{1,2,\cdots ,K\}$表示层号

5.2 用于多关系图的GNN

现实中许多图都有各种边类型，如知识图、AMR图等，可以将其形式化为多关系图。形式上当$|\mathcal{T}|=1,|\mathcal{R}|>1$时，被定义为多关系图。在本节中将介绍不同的技术表示和学习多关系图。

5.2.1 多关系图的形成

由于异质图在NLP领域普遍存在，如知识图、AMR图等，大多数研究者提出将其转换为多关系图，表示为图$\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{T},\mathcal{R})$$|\mathcal{T}|=1,|\mathcal{R}|\ge 1$。为了获得多关系图，技术上忽略了节点类型。至于边，设置初始边的类型为"default"，对于每一个边$e_{i,j}$，为其添加类型为"reverse"的逆向边$e_{j,i}$，并为每个节点添加自环"self"，因此就获得了$|V|=1,|E|=3$的多关系图

5.2.2 多关系GNNs

多关系GNN是经典GNN对多关系图的扩展，其节点类型相同，但边类型不同。它们最初是用来编码特定关系图的，如知识图和解析图，这些图在相同类型的节点之间有复杂的关系。一般来说，大多数多关系GNN采用特定类型的参数对关系进行单独建模。经典的方法有：R-GCN、R-GGNN 和 R-GAT。

1. R-GCN

R-GCN是消息传递GCN框架的自然延伸，该框架在局部图邻域运行，根据标签类型对传入的节点进行分组，然后对每一组分别应用消息传递。因此，节点$v_i$的邻居节点的聚合过程被定义为：
${\mathbf{h}}_i^{(k)}=\sigma \left({\sum }_{r\in \mathcal{E}}{\sum }_{v_j\in N_r\left(v_i\right)}\frac{1}{c_{i,r}}{\mathbf{W}}_r^{(k)}{\mathbf{h}}_j^{(k-1)}+{\mathbf{W}}_0^{(k)}{\mathbf{h}}_i^{(k-1)}\right)$

2. R-GGNN

关系型GGNN最初是用于graph-to-sequence问题开发的，它能够捕捉到长距离的关系。与R-GCN类似，R-GGNN使用特定关系的权重来更好地捕捉节点之间特定关系的相关性。R-GGNN的传播过程可以概括为：
$\begin{array}{rl}{\mathbf{r}}_i^{(k)}& =\sigma \left(\sum _{v_j\in N\left(v_i\right)}\frac{1}{c_{v_i,r}}{\mathbf{W}}_{\varphi \left(e_{i,j}\right)}^r{\mathbf{h}}_j^{(k-1)}+{\mathbf{b}}_{\varphi \left(e_{i,j}\right)}^r\right)\\ {\mathbf{z}}_i^{(k)}& =\sigma \left(\sum _{v_j\in N\left(v_i\right)}\frac{1}{c_{v_i,z}}{\mathbf{W}}_{\varphi \left(e_{i,j}\right)}^z{\mathbf{h}}_j^{(k-1)}+{\mathbf{b}}_{\varphi \left(e_{i,j}\right)}^z\right)\\ {\tilde{h}}_i^{(k)}& =\rho \left(\sum _{v_j\in N\left(v_i\right)}\frac{1}{c_{v_i}}{\mathbf{W}}_{\varphi \left(e_{i,j}\right)}\left({\mathbf{r}}_j^{(k)}\odot {\mathbf{h}}_i^{(k-1)}\right)+{\mathbf{b}}_{\varphi \left(e_{i,j}\right)}\right)\\ {\mathbf{h}}_i^{(k)}& =\left(1-{\mathbf{z}}_i^{(k)}\right)\odot {\mathbf{h}}_i^{(k-1)}+{\mathbf{z}}_i^{(k)}\odot {\tilde{h}}_i^{(k)}\end{array}$

3. R-GAT

Wang等人提出扩展经典的GAT以适应多关系图。直观地说，具有不同关系的邻居节点应该具有不同的影响力。Wang等人（2020b）提出用额外的关系头来扩展同质GAT。从技术上讲，他们提出的关系结点表示为：
${\mathbf{h}}_{i,rel}^{(k),m}={\sum }_{v_j\in N\left(v_i\right)}{\beta }_{ij}^{(k),m}{\mathbf{W}}^{(k),m}{\mathbf{h}}_j^{(k-1)}$

4. Gating Mechanism

多关系GNN在堆叠若干层以利用远处邻居之间的隐性相关性时也面临过平滑问题。为了解决这个问题，在多关系GNN中引入了门控机制，即通过门控将节点的输入特征和聚合特征结合起来。直观地，门控机制可以被看作是原始信号和学习到的信息之间的权衡。它控制传播到下一步的更新消息的数量，从而防止模型彻底覆盖过去的信息。这里以经典的R-GCN为例来介绍门控机制，该机制实际上可以扩展到任意的变体。激活之前的表示为：
${\mathbf{u}}_i^{(k)}=f^{(k)}({\mathbf{h}}_i^{(k-1)})$
其中$f$表示聚合函数。最终，节点的最终表示是先前嵌入${\mathbf{h}}_i^{(k)}$和GNN输出表示$\sigma ({\mathbf{u}}_i^{(k)})$的门控组合：
${\mathbf{h}}_i^{(k)}=\sigma \left({\mathbf{u}}_i^{(k)}\right)\odot {\mathbf{g}}_i^{(k)}+{\mathbf{h}}_i^{(k-1)}\odot \left(1-{\mathbf{g}}_i^{(k-1)}\right)$
其中${\mathbf{g}}_i^{(k)}$是门控函数。计算如下：
${\mathbf{g}}_i^{(k)}=\sigma \left(f^{(k)}\left(\left[{\mathbf{u}}_i^{(k)},{\mathbf{h}}_i^{(k-1)}\right]\right)\right)$

5.2.3 Graph Transformer

Transformer 架构在NLP领域取得了巨大成功，Transformer的自注意力机制是全连接隐式图学习的一个特殊过程，因此GNN和Transformer 的概念产生了连接。然而，传统的 Transformer未能利用结构信息。在GAT的启发下，许多文献通过设计结构感知的自注意力机制，将结构信息纳入Transformer。

1. **自注意力。**形式上将自注意力的输入为：$\mathbf{Q}=\{{\mathbf{q}}_1,{\mathbf{q}}_2,\cdots ,{\mathbf{q}}_n\}\in {\mathbb{R}}^{n\times d^q},\mathbf{K}=\{{\mathbf{k}}_1,{\mathbf{k}}_2,\cdots ,{\mathbf{k}}_n\}\in {\mathbb{R}}^{b\times d^k},\mathbf{V}=\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_n\}\in {\mathbb{R}}^{n\times d^n}$输出为：

$\begin{array}{rl}{\mathbf{z}}_i& =\mathrm{Attention}\left({\mathbf{q}}_i,\mathbf{K},\mathbf{V}\right)=\sum _{j=1}^n{\alpha }_{i,j}{\mathbf{W}}^v{\mathbf{v}}_j\\ {\alpha }_{i,j}& ={\mathrm{softmax}}_j\left(u_{i,j}\right)\\ u_{i,j}& =\frac{{\left({\mathbf{W}}^q{\mathbf{q}}_i\right)}^T\left({\mathbf{W}}^k{\mathbf{k}}_j\right)}{\sqrt{d}}\end{array}$
对于图 transformer 来说，query、key和value都是指节点的嵌入：即${\mathbf{q}}_i={\mathbf{k}}_i={\mathbf{v}}_i={\mathbf{h}}_i$。
对于包含结构知识的关系图，有各种图transformer，根据自注意力的功能可以分为两类。

• 一类是基于R-GAT的方法，它采用类似关系GAT的特征聚合方式。
• 另一类是保留全连接图，同时将结构感知关系信息融合到到自注意函数中。

2. R-GAT Based Graph Transformer

基于GAT的图transformer采用了类似GAT的特征聚合，它利用了图连接性的归纳偏置。在技术上，首先用特定类型的聚合步骤聚合邻居，然后通过前馈层进行融合，具体如下：
$\begin{array}{rl}{\mathbf{z}}_i^{r,(k)}& =\sum _{v_j\in N_r\left(v_i\right)}{\alpha }_{i,j}^k{\mathbf{W}}^{v,(k)}{\mathbf{h}}_j^{(k-1)},r\in \mathcal{E}\\ {\mathbf{h}}_i^{(k)}& ={\mathrm{FFN}}^{(k)}\left({\mathbf{W}}^{O,(k)}\left[{\mathbf{z}}_i^{R_1,(k)},\dots ,{\mathbf{z}}_i^{R_q,(k)}\right]\right)\end{array}$
其中${\mathrm{F}\mathrm{F}\mathrm{N}}^{(k)}(\cdot )$表示Transformer中的前馈层

3. Structure-aware Self-attention Based Graph Transformer

基于结构感知的自注意的图transformer保留了原有的自注意架构，允许非邻接节点的通信。首先讨论结构感知的自我注意机制，然后介绍其独特的边嵌入表示法。
Shaw等人尝试对神经机器翻译(NMT)任务中单词（节点）之间的相对关系进行建模。在技术上，他们在计算节点相似度时考虑了关系嵌入：
$u_{i,j}^{(k)}=\frac{{\left({\mathbf{W}}^{q,(k)}{\mathbf{h}}_i^{(k-1)}\right)}^T\left({\mathbf{W}}^{k,(k)}{\mathbf{h}}_j^{(k-1)}\right)+{\left({\mathbf{W}}^{q,(k)}{\mathbf{h}}_i^{(k-1)}\right)}^T{\mathbf{e}}_{i,j}}{\sqrt{d}}$

5.3 GNN for Heterogeneous Graph

现实中的大多数图有多种节点和边的类型，如知识图谱，AMR图，它们被称为异质图。从形式上看，对于一个图$\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{T},\mathcal{R})$$|\mathcal{T}|>1$或者$|\mathcal{R}|>1$，那么称其为异质图。除了将异质图转化为关系图外，如上一小节所介绍的，有时还需要充分利用节点和边的类别信息。因此，在第5.3.1小节中，首先介绍了异质图的预处理技术。然后，在第5.3.2和5.3.3小节中，将介绍两种专门针对异质图的典型图表示学习方法。

5.3.1 LEVI 图转换技术

大多数现有的GNN方法只针对同质条件而设计，在处理大量的边类型时，会有大量的计算负担（例如，一个AMR图可能包含100多种边类型），因此，在异质图中有效的做法是将边视为节点。最重要的图转换技术是Levi Graph Transformation，对于每一个具有特定标签$\varphi (e_{i,j})$的边$e_{i,j}$，创建一个新的节点$v_{e_{i,j}}$得到一个新图${\mathcal{G}}^{\prime }({\mathcal{V}}^{\prime },{\mathcal{E}}^{\prime },{\mathcal{T}}^{\prime },{\mathcal{R}}^{\prime })$其中节点集${\mathcal{V}}^{\prime }=\mathcal{V}\cup \{v_{e_{i,j}}\}$节点标签集${\mathcal{T}}^{\prime }=\mathcal{T}\cup \{\varphi (e_{i,j})\}$。切断了$v_i,v_i$之间的直接边，并添加两直接边：1）$v_i,v_{e_{i,j}}$，和2）$v_{e_{i,j}},v_j$。在转换$\mathcal{E}$中的所有边之后，新的图${\mathcal{G}}^{\prime }$是一个二分图，且$|{\mathcal{R}}^{\prime }|=1$。图11给出了将AMR图转换为levi示例图，它具有单一的边类型，但节点类型不受限制，然后可以由第5.3小节中描述的异质GNN进行学习。

5.3.2 基于元路径的异质 GNN

1. Meta-path

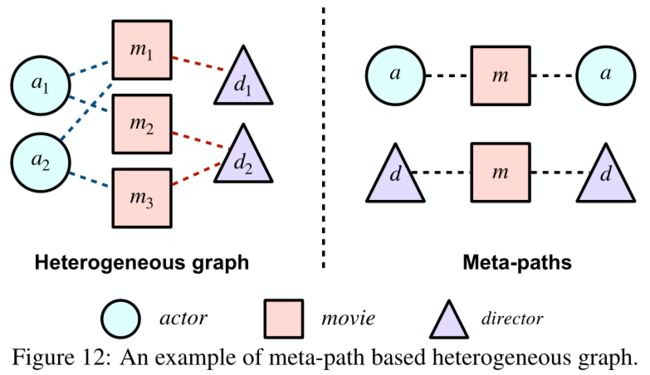
元路径是连接两个对象的复合关系，是一种广泛使用的捕捉语义的结构。以电影数据IMDB为例，有三种类型的节点，包括电影、演员和导演。元路径Movie → Actor →Movie，涵盖了两部电影和一个演员，描述了co-actor的关系。因此，异质图中节点之间的不同关系可以很容易地通过元路径展示出来。首先提供了异质图的meta-level 描述，以便更好地理解。
遵循异质信息网络（HIN）的设定，给出了网络模式的概念。网络模式是异质图$\mathcal{G}(\mathcal{V},\mathcal{E})$的元模板：节点类型映射$\mathcal{V}\to \mathcal{T}$以及边类型映射$\mathcal{T}\to \mathcal{R}$，网络模式上的元路径表示为$\Phi =T_1\stackrel{R_1}{\to }{T}_2\stackrel{R_2}{\to }\dots \stackrel{R_l}{\to }{T}_{l+1}$， $T_i\in \mathcal{T}$是模式的节点，$R_i\in \mathcal{R}$是对应的关系节点。元路径集合为$\{{\Phi }_1,{\Phi }_2,\cdots ,{\Phi }_p\}$。对于异质图的节点$v_i$以及一个元路径${\Phi }_j$ ，定义基于元路径的邻居为$N_{{\varphi }_j}(v_i)$，基于元路径的异质图的示例如图12所示。根据元路径的长度邻居集可以有多跳节点。
大多数基于元路径的GNN方法采用基于注意力的聚合策略。它们一般可以分为两个阶段。

• 1）沿着每条元路径聚合邻居，“节点级聚集”。节点通过不同的元路径接收邻居的信息
• 2）应用元路径级别的注意力机制来学习不同元路径的语义影响。可以学习由多条元路径连接邻居的最佳组合。

2. HAN

由于节点的异质性，不同的节点具有不同的特征空间，这给GNN处理各种初始节点嵌入带来了很大挑战。为解决这一问题，采用特定类型的变换将各种节点投射到统一的特征空间：
${\mathbf{h}}_i^{\prime }={\mathbf{W}}_{\tau \left(v_i\right)}{\mathbf{h}}_i$

• Node-level Aggregation：对于在元路径上节点的邻居节点集合，节点特征的聚合过程可以表示为：
• $\begin{array}{rl}{\mathbf{z}}_{i,{\Phi }_k}& =\sigma \left(\sum _{v_j\in N_{{\Phi }_k}\left(v_i\right)}{\alpha }_{i,j}^{{\Phi }_k}{\mathbf{h}}_j\right)\\ {\alpha }_{i,j}^{{\Phi }_k}& ={\mathrm{softmax}}_j\left(u_{i,j}^{{\Phi }_k}\right)\\ u_{i,j}^{{\Phi }_k}& =\mathrm{Attention}\left({\mathbf{h}}_i,{\mathbf{h}}_j;{\Phi }_k\right)=\sigma \left(\mathbf{W}\left[{\mathbf{h}}_i,{\mathbf{h}}_j\right]\right)\end{array}$
• Meta-path Level Aggregation：一般来说，不同的元路径传达了不同的语义信息。为此，旨在学习每个元路径的重要性：

$({\beta }_{{\varphi }_1},\cdots ,{\beta }_{{\varphi }_p})=\mathrm{M}\mathrm{e}\mathrm{t}\mathrm{a}\_\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{n}({\mathbf{Z}}_{{\varphi }_1},\cdots ,{\mathbf{Z}}_{{\varphi }_{\mathbf{p}}})$

• 对于每条元路径，首先学习每个节点的语义级重要性。然后对它们进行平均，得到元路径级别的重要性：

$\begin{array}{l}{O}_{{\Phi }_k}=\frac{1}{|\mathcal{V}|}{\sum }_{v_i\in \mathcal{V}}{\mathbf{q}}^{T}f\left({\mathbf{z}}_{i,{\Phi }_k}\right)\\ {\beta }_{{\Phi }_k}=\mathrm{softmax}{}_k\left(o_{{\Phi }_k}\right)\end{array}$

• 最终获得节点表示:

${\mathbf{z}}_i={\sum }_{k=1}^p{\beta }_{{\Phi }_k}{\mathbf{z}}_{i,{\Phi }_k}.$

5.3.3 基于R-GNN的异质GNN

尽管元路径是组织异质图的有效工具，但它需要额外的领域专家知识。为此，大多数研究人员通过使用特定类型的聚合，采用了R-GNN的类似想法。为了清楚起见，本文将这些方法命名为基于R-GNN的异质GNN，下文介绍这一类的几个典型变体。

1. HGAT
   • HGAT（Linmei等人，2019）被提出用于编码包含各种节点类型但单一边类型的异质图。换句话说，边只代表连接性。对于一个特定的节点，不同类型的邻居可能有不同的相关性。为了充分利用多样化的结构信息，HGAT首先专注于全局类型的相关性学习，然后学习具体节点的表示
   • 类型级别学习。对于具体节点$v_i$及其邻居$N(v_i)$，HGAT得到特定类型的邻居表示为：

${\mathbf{z}}_t^{(k)}={\sum }_{v_j\in N_t\left(v_i\right)}{\mathbf{h}}_j^{(k-1)},t\in \mathcal{T}$

  - 重写具有节点类型$t$的邻居$N(v_i)$。然后为注意机制计算每个类型的相关性：

$\begin{array}{rl}{s}_t& =\sigma \left({\mathbf{q}}^T\left[{\mathbf{h}}_i^{(k-1)},{\mathbf{z}}_t^{(k)}\right]\right)\\ {\alpha }_t& =\frac{\exp \left(s_t\right)}{{\sum }_{t^{\prime }\in \mathcal{T}}\exp \left(s_{t^{\prime }}\right)}\end{array}$

• 节点级别学习。对不同类型的节点应用R-GCN聚合过程。形式上，对于节点$v_i$及类型相关性$\{{\alpha }_t\},t\in \mathcal{T}$，HGAT计算每个邻居的注意力得分如下：
• $\begin{array}{rl}{b}_{i,j}& =\sigma \left({\mathbf{q}}_1^T{\alpha }_{\tau \left(v_j\right)}\left[{\mathbf{h}}_i^{(k-1)},{\mathbf{h}}_j^{(k-1)}\right]\right)\\ {\beta }_{i,j}& =\frac{\exp \left(b_{i,j}\right)}{{\sum }_{v_m\in N\left(v_i\right)}\exp \left(b_{i,m}\right)}\end{array}$
  • 最后，HGAT应用分层异质GCN来学习节点表示：
• ${\mathbf{h}}_i^{(k)}=\sigma \left({\sum }_{t\in \mathcal{T}}{\sum }_{v_j\in N_t\left(v_i\right)}{\mathbf{W}}_t^{(k)}{\mathbf{h}}_j^{(k-1)}\right)$

2. MHGRN
   • MHGRN（Feng等人，2020b）是R-GCN的一个扩展，它可以直接在异质图上利用多跳信息。通常，借助关系路径（如元路径）的思想来建模两个不具有k-hop连接节点的关系，并将现有的R-GNN扩展到基于路径的异质图表示学习范式。节点$v_i,v_j$之间的k-hop关系路径表示为:
   • ${\Phi }_k=\left\{\left(v_i,e_{i,1},\dots ,e_{k-1,j},v_j\right)\mid \left(v_i,e_{i,1},v_1\right),\dots ,\left(v_{k-1},e_{k-1,j}\right)\in \mathcal{E}\right\}$
3. HGT
   • HGT（Hu, 2020a）是异质图的图transformer，它在网络模式之上建立节点之间的元关系，正如在基于元路径的异质GNN段落中讨论的那样。与之前大多数假设图结构是静态的（即与时间无关）的工作不同，提出了一个相对的时间编码策略来学习时间依赖性。

6. 基于GNN 的编码器-解码器模型

编码器-解码器架构是NLP领域最广泛使用的机器学习框架之一，如Seq2Seq模型。鉴于GNN在建模图结构数据方面的巨大力量，最近，许多研究设计了基于GNN的编码器-解码器框架，包括Graph-to-Tree和Graph-to-Graph。本节首先介绍典型的Seq2Seq模型，然后讨论用于各种NLP任务的各种基于图的编码器-解码器模型。

图11 基于图的编码器解码器模型总体架构

6.1 Sequence-to-Sequence Models

首先对Seq2Seq学习进行了简要的概述，并介绍一些典型的Seq2Seq技术。然后指出Seq2Seq学习的一些已知的局限性以及它的解决方案，即纳入更多结构化的编码器-解码器模型作为原始Seq2Seq模型的替代，以编码更复杂的数据结构。

6.1.1 介绍

Seq2Seq模型用于解决一般的序列到序列问题（如机器翻译）。Seq2Seq模型是一个端到端的编码器-解码器框架，它学习将一个可变长度的输入序列到一个可变长度的输出序列。通常其思想是使用基于RNN的编码器来读取输入序列，建立一个固定维度的向量表示，然后使用基于RNN的解码器来生成基于编码器输出向量的输出序列。解码器本质上是一个RNN语言模型，只不过它取决于输入序列。最常见的Seq2Seq变体之一是应用双向LSTM编码器对输入序列进行编码，并应用LSTM解码器对输出序列进行解码。其他Seq2Seq变体用门控递归单元（GRU）、卷积神经网络（CNN）或 Transformer模型代替LSTM。
在最初的Seq2Seq架构中，中间向量的表示成为信息瓶颈，因为它将输入序列的丰富信息总结为固定维度的嵌入，作为解码器生成高质量输出序列的唯一知识源。为了提高原始Seq2Seq模型的学习能力，人们提出了许多有效的技术。

6.1.2 方法

注意力机制被设计用来学习输入序列和输出序列之间的软对齐。具体地，在每个解码步骤$t$，指示源词上的概率分布的attention向量被计算为:
$\begin{array}{rl}{e}_i^t& =\mathrm{f}\left(h_i,s_t\right)\\ a^t& =\mathrm{softmax}\left(e^t\right)\end{array}$
其中$f$可以是计算解码器状态$s_t$和编码器隐藏状态状态$h_i$之间的相关性的任意神经网络。一种常见的选择是使用加法注意机制$\mathrm{f}\left(h_i,s_t\right)=v^T\tanh \left(W_h{h}_i+W_s{s}_t+b\right)$。给定第$t$个解码步骤的attention向量$a^t$，可以将上下文向量计算为编码器隐藏状态的加权和，公式如下:
$h_t^{\ast }={\sum }_i{a}_i^t{h}_i$
所计算的上下文向量将与解码器状态连接，并通过一些神经网络反馈，以产生词汇分布。

6.1.3 讨论

许多NLP应用自然地接纳了图结构的输入数据，如依赖图、构成图，AMR图，IE图和知识图。与序列数据相比，图结构的数据能够编码对象之间丰富的句法或语义关系。此外，即使原始输入最初是以序列形式表示的，它仍然可以从显式地将结构信息（例如特定领域知识）结合到序列中去。上述情况基本上需要一个编码器-解码器框架来学习图到X的映射，其中X可以代表序列、树或甚至图。现有的Seq2Seq模型在学习从图到适当目标的精确映射方面面临着巨大挑战，因为它无法建模复杂的图结构化数据。
为了扩展Seq2Seq模型以处理输入为图结构数据的Graph-to-Sequence问题，进行了各种尝试。一个简单直接的方法是直接将结构化图数据线性化为序列数据，并将Seq2Seq模型应用于所得序列。然而这遭受巨大的信息损失，导致了性能的下降。RNN没有能力对复杂的结构化数据进行建模的根本原因在于RNN是一个线性链。因此一些研究工作已经致力于扩展Seq2Seq模型。
例如，Tree2Seq（Eriguchi, 2016）通过采用Tree-LSTM扩展了Seq2Seq模型，Tree-LSTM是链结构LSTM到树结构网络拓扑的推广。Set2Seq是Seq2Seq模型的一个扩展，它超越了序列，使用注意力机制处理输入集。
尽管这些Seq2Seq扩展在某些类别的问题上取得了有希望的结果，但它们都不能以一种原则性的方式对任意图结构的数据进行建模。

6.2 Graph-to-Sequence Models

6.2.1 综述

为了解决上述Seq2Seq模型在编码丰富复杂的数据结构上的局限性，最近提出了一些用于NLP任务的graph-to-sequence的编码器-解码器模型。Graph2Seq模型通常采用基于GNN的编码器和一个基于RNN/Transformer的解码器。与Seq2Seq范式相比，Graph2Seq范式更善于捕捉输入文本的丰富结构信息，可以应用于任意的图结构数据。与Seq2Seq模型相比，Graph2Seq模型在广泛的NLP任务中显示出优越的性能，包括神经机器翻译，AMR-to-text、文本摘要、问题生成、KG-to-text、SQL-to-text、code summarization和语义解析。

6.2.2 方法

1. 基于图的编码器

早期的Graph2Seq方法及其后续工作主要使用一些典型的GNN变体作为图编码器，包括GCN、GGNN、GraphSAGE和GAT。由于NLP图中的边方向经常编码关于两个顶点之间的语义关系的关键信息，因此捕获文本的双向信息往往是非常有帮助的。在Graph2Seq范式的文献中，一些工作扩展现有的GNN模型以处理有向图。最常见的策略是在进行邻居聚合时，为不同的边方向（即传入/传出/自环边）引入单独的模型参数。
除了边方向信息，NLP应用中的许多图实际上是多关系图，其中边类型信息对下游任务非常重要。一些工作通过为不同的边类型设置单独的模型参数来编码边类型信息。然而许多NLP应用中（如KG相关任务），边类型的总数很大，因此上述策略会有严重的可扩展性问题。为此一些工作提出通过将多关系图转换为Levi图来绕过这个问题，然后利用现有为同质图设计的GNN作为编码器。另一个普遍采用的技术是将边嵌入显示地纳入消息传递机制。
除了上述广泛使用的GNN变体外，一些Graph2Seq工作还探索了其他GNN变体，如GRN和GIN。GRN能够通过在LSTM样式的消息传递机制中显式地包含边嵌入来处理多关系图。

2. 节点/边嵌入初始化

对于基于GNN的方法，节点和边的初始化很重要。虽然CNNs和RNNs都擅长捕捉文本中连续词之间的局部依赖关系，但GNNs在捕捉图中相邻节点之间的局部依存性表现良好。许多关于Graph2Seq的工作表明，在应用基于GNN的编码器之前，将CNN或双向RNN对词嵌入序列初始化节点/边嵌入。还有研究探索用BERT嵌入+BiRNNs或RoBERTa+BiRNNs初始化节点/边嵌入。

3. 序列解码技术

由于Seq2Seq和Graph2Seq模型的主要区别在于编码器，Seq2Seq模型中使用的常见解码技术，如注意力机制、copying机制、coverage机制和scheduled sampling也可以在Graph2Seq模型中采用。常见的解码技术适应Graph2Seq范式如下:

• 为了将包含多token序列的整个节点属性从输入图复制到输出序列，Chen等人（2020h）将token级copying机制扩展到节点级copying机制。
• 为了结合序列编码器和图编码器的优点，Pan等人(2020),Sachan等(2020)在将输出送入解码器之前将其融合为一个单一的向量。
• Huang等人(2020b)分别为序列编码器和图编码器设计了独立的注意力模块。

6.2.3 讨论

Graph2Seq模型和基于Transformer的Seq2Seq模式之间存在一些联系和差异。然而最近有一种趋势是将这两种范式的优点结合起来，从而使它们变得不那么明显。许多工作设计了各种基于graph transformer的生成模型，这些模型采用了结合GNN和transformer优点的基于图的编码器，以及基于RNN/transformer的解码器。Graph2Seq仍存在一些挑战。

• 将GNN应用于图表示学习的常见挑战
  • 如何更好地建模多关系或异质图
  • 如何扩展到大规模图（如知识图）
  • 如何进行联合图结构和表示学习
  • 如何解决过度平滑问题等
• Graph2Seq模型还继承了Seq2Seq模式所面临的挑战
  • 如何解决基于交叉熵的序列训练的局限性（如暴露偏差以及训练和推理阶段之间的差异）。

6.3 Graph-to-Tree Models

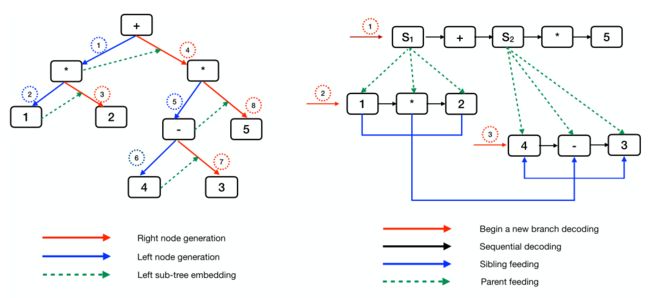
图14：等式:(1*2)+(4-3)*5。左：基于DFS的树解码器示例，数字代表解码操作的顺序。右：基于BFS的树解码器示例。像$S_1$、$S_2$这样的节点代表子树节点，一旦生成了子树节点，解码器将为新的后代解码过程启动新的分支。该数字表示不同分支解码过程的顺序。

6.3.1 综述

与在输入端考虑结构信息的Graph2Seq模型相比，许多NLP任务还包含复杂结构表示的输出，如Tree在输出端也有丰富的结构信息，如句法解析，语义解析，数学单词问题解决。考虑输出的结构信息很有必要。一些Graph2Tree模型被提出来，在输入和输出端都加入了结构信息，使编码-解码过程中的信息流更加完整。

6.3.2 方法

1. 图构造

图构建模块通常与特定任务高度相关，可分为两类**：**

• (1)具有辅助信息：Li等人(2020b)在语义解析和数学单词问题解决任务中都使用了句法图，该句法图由原始句子和句法pasing树（依赖和选区树）组成
• 另一类没有辅助信息。Zhang等人(2020c)在图构建模块中的数学单词问题中使用了不同数字之间的关系。

2. 图编码器

图编码器用于将输入图嵌入到潜在表示中。为了实现图编码器模块，几个Graph2Tree模型使用简单GNN模型，例如GCN、GGNN和GraphSAGE。

3. 注意力

注意力模块是编码器-解码器框架中的一个关键组件，承载了桥接输入和输出语义的重要信息。在Graph2Tree模型中，输入图通常包含不同类型的节点，而传统的注意力模块无法区分这些节点。Li等人(2020b)使用单独的注意力模块来计算输入图中不同节点的注意力向量，其中一些节点来自原始句子，其他节点由外部解析器生成的解析树中的节点组成。区分这两种类型的节点可以比原始的注意力模块促进更好的学习过程。这种想法类似于Tree2Seq（Eriguchi等人，2016）注意模块在机器翻译中的应用。
特别是在（Li等人，2020b）中，解码器通过将一些分支节点表示为非终端节点来生成树结构，即图14中的节点$S_1$。一旦生成这些节点，解码器将开始新的序列解码过程。在时间$t$处的解码器隐藏状态$s_t$被计算为:
${\mathbf{s}}_t=f_{\text{decoder }}\left(y_{t-1},{\mathbf{s}}_{t-1};{\mathbf{s}}_{\text{par }};{\mathbf{s}}_{\text{sib }}\right)$
如图14所示。在生成当前隐藏状态后，包括注意力层的输出模块计算如下
$\begin{array}{rl}{\alpha }_{t(v)}=& \frac{\exp \left(\mathrm{score}\left({\mathbf{z}}_v,{\mathbf{s}}_t\right)\right)}{\exp \left({\sum }_{k=1}^{V_1}\mathrm{score}\left({\mathbf{z}}_k,{\mathbf{s}}_t\right)\right)},\forall v\in {\mathcal{V}}_1\\ {\beta }_{t(v)}=& \frac{\exp \left(\mathrm{score}\left({\mathbf{z}}_v,{\mathbf{s}}_t\right)\right)}{\exp \left({\sum }_{k=1}^{V_2}\mathrm{score}\left({\mathbf{z}}_k,{\mathbf{s}}_t\right)\right)},\forall v\in {\mathcal{V}}_2\\ {\mathbf{c}}_{v_1}=& \sum {\alpha }_{t(v)}{\mathbf{z}}_v,\forall v\in {\mathcal{V}}_1\\ {\mathbf{c}}_{v_2}=& \sum {\beta }_{t(v)}{\mathbf{z}}_v,\forall v\in {\mathcal{V}}_2\end{array}$

4. 树解码器

一些应用程序（即语义解析、代码生成和数学单词问题）的输出包含结构信息，例如，数学单词问题中的输出是一个数学方程，可以通过树的数据结构自然地表达。为了生成这些类型的输出，树解码器被广泛用于这些任务。树解码器可以分为两个主要部分，如图14所示，即基于dfs（深度优先搜索）的树解码器和基于bfs（广度优先搜索）树解码器。

• 基于bfs的解码器，主要思想是将树中的所有子树表示为非终端节点，然后使用序列解码生成中间结果。如果结果包含非终端，那么开始分支（开始新的解码过程），将此节点作为新的根节点，直到整个树展开。
• 基于dfs的解码器，将整个树生成过程视为一系列操作。例如，在Zhang（2020c）中生成二叉树（数学方程）时，在每个步骤中优先生成根节点，然后生成左子节点。在生成所有左子节点之后，采用自下而上的方式开始生成右子节点.

此外，树解码器不断发展，提出了一些技术来在解码过程中收集更多信息或利用来自输入或输出的信息，例如父馈送、兄弟馈送、子树复制、基于树的重新排序和其他技术。同时，变换器模型的广泛应用也带来了许多基于变换器的树解码器，这证明了树解码器和Graph2tree模型的广泛使用。

6.4 Graph-to-Graph Models

graph-to-graph模型通常用于解决graph transformation问题，是图编码器-解码器模型。图编码器生成图中每个节点的潜在表示，或通过GNNs为整个图生成一个图级别潜在表示。然后图解码器根据来自编码器的节点级或图级潜在表示生成输出目标图。

1. Graph-to-graph transformation

图到图模型旨在处理深度图转换问题。图转换的目标是通过深度学习将源域中的输入图转换为目标域中的相应输出图。作为一个新的重要问题，深度图转换在许多领域都有多种应用，例如网络安全中的分子优化和恶意软件限制。考虑到在转换过程中正在转换的实体，有三类子问题：

• 节点转换：输入图中的节点集或节点属性可以在转换过程中更改
• 边转换：输入图中的图拓扑或边属性可以在变换过程中更改
• 节点-边联合转换：节点和边的属性都可以更改。

2. Graph-to-Graph for NLP

由于自然语言或信息知识图可以形式化为一组节点及其关系的图，因此NLP领域中的许多生成任务可以形式化为graph-to-graph问题，这可以通过图到图模型进一步解决。这样可以充分利用和捕获输入和输出句子的语义结构信息。两个重要的NLP任务（即信息提取和语义解析），可以形式化为图对图问题

• 用于信息提取的图变换

信息提取是从文本中提取结构化信息，通常包括名称实体识别、关系提取和共同引用链接。信息提取问题可以形式化为一个图转换问题，输入是文本的依赖图或选区图，输出是信息图。在输入依赖关系或选区图中，每个节点表示一个单词token，每个边表示两个节点之间的依赖关系。在输出信息图中，每个节点表示一个名称实体，每个边表示两个实体之间的语义关系或共同引用链接。
以这种方式，信息提取是关于在给定输入相关性或选区图的情况下生成输出信息图。

• 用于语义解析的图转换

语义分析的任务是将自然语言映射到机器可解释的意义表示，而这些意义表示又可以用许多不同的形式表示，包括lambda演算、基于依赖的组合语义、框架语义、抽象意义表示（AMR）、最小递归语义和话语表示理论。显式或隐式地，这些形式中的任何一种表示都可以表示为有向无环图（DAG）。
语义解析也可以形式化为一个图转换问题，其中输入是依赖关系图或选区图，输出是语义的有向无环图。例如，AMR的语义形式可以编码为根的、有向的、非循环图，其中节点表示概念，标记的有向边表示它们之间的关系。
序列到图的转换可以被视为图到图的特殊情况，其中输入序列是一个线图。序列到图模型通常用于AMR分析任务，其目标是学习从句子到AMR图的映射。为了生成具有索引节点的AMR树，解析方法被形式化为两个阶段：节点预测和边预测。整个过程由指针网络实现，其中编码器是多层双向RNN，目标图中的节点按顺序预测。之后，基于学习到的结束节点的嵌入来预测每对节点之间的边。

7. 应用

本章将讨论大量使用GNN的典型NLP应用，包括自然语言生成NLG、机器阅读理解、问题回答、对话系统、文本分类、文本匹配、话题建模、情感分类、知识图谱、信息提取IE、语义和句法解析、推理和语义角色标注。表3中提供了所有应用的摘要及其子任务和评价指标。

7.1 自然语言生成

自然语言生成（NLG）旨在给定各种形式的输入，如文本、语音等，生成高质量、连贯和可理解的自然语言，而我们只关注语言形式。现代NLG方法通常采取编码器-解码器的形式，将输入序列编码到潜在空间，并根据潜在表征预测出一个词的集合。大多数NLG方法可以分为两个步骤：编码和解码，它们由两个模块处理：编码器和解码器。本节对基于auto-regressive图的方法进行了全面的概述，这些方法利用了编码器中的图结构，包括：1）神经机器翻译，2）摘要，3）问题生成，4）structural-data to text。

7.1.1 神经机器翻译

背景和动机 经典的神经机器翻译（NMT）系统旨在将源语言的句子映射到目标语言，而不改变其语义。大多数工作采用了基于注意力的seq2seq学习图，特别是基于RNN的语言模型。与传统的机器翻译模型相比，这些方法可以在没有特定语言知识的情况下产生更好的性能。然而这些方法存在着长依赖性的问题。随着注意力机制的发展，完全基于注意力的模型，如Transformer，通过自注意力捕捉隐性关联，达到了新的水平。虽然这些取得了巨大的成功，但它们很少考虑到结构信息，如句法结构。最近在GNN的帮助下，许多研究者通过挖掘非结构化文本中包含的结构性知识进一步提升了性能。
方法 大多数基于GNN的NMT方法将传统的seq2seq图转换成Graph2Seq架构。首先将输入文本转换为图结构的数据，然后采用基于GNN的编码器来利用结构信息。

1. 图构造

NMT任务中引入各种静态图以应对相应的挑战。Bastings et al (2017); Beck et al (2018b); Cai and Lam (2020b); Guo et al (2019b)首先将给定文本转换为句法依存图。这种结构没有考虑单词的语义关系。直观上，通过高级语义结构抽象来表示冗余句子是有益的。为此Marcheggiani et al (2018)为给定文本构建了基于语义角色标记的依赖图。此外Beck et al (2018b); Song et al (2019)构建了可以涵盖更多语义相关性的句子AMR图。除了经典的图类型之外，还提出了一些专门设计的图（应用驱动图）来解决这些独特的挑战。
虽然NMT中的源句子是确定的，但单词级别或子单词级别分段有多种选择，可以用不同的单词段或不同的子单词词汇大小来分割源序列，这会影响NMT的性能。Xiao(2019)提出了格图，它结合了源句子的不同分割。Shaw et al (2018)构建相对位置图，以显式地建模相对位置特征。Yin et al (2020）构建了多模态图，将视觉知识引入NMT，NMT在统一的图中呈现输入句子和相应的图像，以更好地捕捉语义相关性。
尽管是单一类型的静态图，Xu et al (2020b)为文档级NMT构建了考虑多个关系的混合图，以解决严重的长依赖性问题。详细地，他们构建了同时考虑句内和句间关系的图。对于句内关系，它们将单词与顺序关系和依存关系联系起来。对于句子间关系，他们将不同句子中的单词与词汇（重复或相似）和共指关联联系起来。

2. 图表示学习

大多数构造图都是异质图，包含多种节点/边类型，不能被典型的GNN直接利用。研究人员采用了各种异质图表示技术。

• Bastings et al (2017); Marcheggiani et al (2018)将依赖图视为多关系图，并应用有向GCN来学习图表示。
• Beck et al (2018b)首先将构建的多关系图转换为levi图，并应用关系GGNN，该GGNN使用边缘类型特定参数来利用丰富的结构信息。
• Xu et al (2020b)将边视为连通性，并将边方向视为边类型，如“向内”、“向外”和“自我”。然后，他们应用关系GCN对文档图进行编码。
• Guo et al (2019b)将异质图转换为levi图，并采用密集连接GCN来学习嵌入。
• Song et al (2019)提出了一种特殊的类型感知异质GGNN，以联合学习节点嵌入和边嵌入。具体来说，他们首先通过融合源节点和边类型的嵌入来学习边表示。然后聚合来自其传入和传出邻居的表示，并利用基于RNN的模块来更新节点表示。

除了传统GNN的扩展，Transformer还被进一步探索以从NMT的结构输入中学习。与传统的Transformer不同，采用绝对正弦位置嵌入来确保自注意力学习特定位置的特征。

• Shaw et al (2018); Xiao et al (2019)采用基于位置的边嵌入来捕获位置相关性，并使Transformer从基于图的输入中学习。
• Cai和Lam(2020b)学习了基于双向路径的关系嵌入，并在计算自注意力时将其添加到节点嵌入中。然后从给定的图中找到任意两个节点的最短路径，并应用双向GRU对路径进行进一步编码，以获得关系表示。
• Yin et al (2020)应用基于graph-transformer的编码器学习多模态图。首先，通过对单词嵌入和位置嵌入的和得到文本模态的节点的初始嵌入，应用MLP层将视觉节点作为文本节点投影到统一空间。其次，应用多头自注意力来学习每个模态内表示。第三，使用基于GAT的跨模态融合来学习跨模态表示。

3. 特殊技术

为了允许信息从两个方向流动，一些技术被设计用于合并方向信息。

• Bastingset al (2017)；Marcheggiani et al (2018)；Beck et al (2018b)将相应的反向边添加为额外的边类型"reverse"，自循环边类型也添加为"self"。
• Guo et al (2019b)首先添加一个全局节点，从该全局节点到其他节点的边用类型"global"标记。此外，还在输入文本中存在的节点之间添加了类型为"forward"和"backward"的双向顺序链接。

**基准和评价 **NMT的常见基准包括用于训练的News Commentary v11, WMT14, WMT16, WMT19，用于评估和测试的newstest2013, newstest2015, newstest2016, newsdev2019, newstest2019。对于多模态NMT任务，先前的工作广泛使用了Multi30K数据集。BLEU是评价生成的文本和真实输出文本之间的相似性的典型指标。

7.1.2 摘要生成

背景和动机 自动摘要生成是在保留关键信息内容和整体意义的同时，生成简明流畅的摘要。这个任务有两个主要的经典设置

• 1）抽取式摘要：侧重于从给定文本中选择子句以减少冗余，这被表述为一个分类问题
• 2）生成式摘要：遵循神经语言生成任务。它通常采用编码器-解码器架构来生成文本摘要。与抽取式相比，抽象式设置更具挑战性且更具吸引力，因为它可以生成不存在的表达式。

传统的方法将输入视为序列，并应用LSTM、Transformer等编码器学习潜在表示，这些方法未能利用自然输入中隐含的丰富结构信息。许多研究人员发现，结构知识有利于解决一些挑战，例如长距离依赖性问题，因此提出了基于GNN的技术显示利用结构信息来提高性能。
大多数基于GNN的摘要方法首先是构建图来表示给定的文本。然后，采用基于GNN的编码器来学习图的表示。之后，对于抽取式摘要模型，采用分类器来选择候选子句来组成最终的总结。对于生成式摘要，大多采用语言解码器，以最大化输出的可能性来生成摘要。
方法 首先构建图来表示给定的自然文本。然后使用基于GNN的编码器来学习图表示。之后对于抽取式摘要采用分类器来选择候选子内容以构成最终摘要。对于生成式摘要采用最大化输出可能性的语言解码器来生成摘要

1. **图构造：**介绍了为不同类型的输入（包括单文档、多文档和代码）构建合适且有效的图的不同方法
   1. 单文档
      • Fernandes et al(2019)构建了混合图，包括顺序和共指关系。
      • 为了解决语义不相关和偏差等问题，Jin et al(2020b)构建了语义依赖图，并将其转换为给定文本的多关系图。
      • 为了捕获文档级摘要中典型的长依赖性，Xu et al(2020a)构建了混合图。首先通过RST解析构建话语图，然后在文档中的共同引用提及之间添加共同引用边。
      • 为了更好地捕捉句子层次上的长依赖关系并丰富语义相关性，Wang et al(2020a)将句子和包含词视为节点，并构建相似度图来建模语义关系。
      • 为了建模句子之间的冗余关系，Jia et al(2020)提出构建混合异质图，该图包含三种类型的节点：1）命名实体、2）单词和3）句子，以及四种类型的边：1）sequential、2）containing、3）same和4）similar。
      • 为了考虑句间关系尤其是主题信息。Cui et al(2020b)和Zhao et al(2020)通过引入额外的主题词来发现潜在的主题信息来构建主题图。Zhao et al(2020c)挖掘非主题节点的子图，以表示原始文本，同时保留主题信息。
   2. 多文档
      • Yasunaga et al(2017)将文档聚类分解为句子，并通过个性化话语图算法构建话语图。
      • Li et al(2020c)将文档分成段落，并构建三个单独的图：1）相似度图、2）话语图和3）主题图。
   3. 代码
      • Fernandes et al(2019)为给定的程序剪辑构建了特定的代码图。首先通过编程语言启发式将标识符标记（即变量、方法等）分解为子标记。然后构建图，根据顺序位置和词汇用法组织子标记。
      • LeClair et al(2020)将给定程序解析为抽象语法树（AST），然后将其转换为程序图。
2. **图表示学习：**同质GNN和异质GNN都被用来学习图表示。
   1. 对于同质图
   • Li et al(2020c)应用基于自关注的GA T来学习全连通图上的表示。具体来说，他们引入高斯核来从图的拓扑中挖掘节点之间的边缘重要性。
   • Zhao et al(2020c)采用了基于GAT的图变换器，该变换器将通过自我关注学习到的相似性视为边缘权重。
   2. 对于异质图，一些工作通过特殊技术将异质图转换为同质图。
   • LeClair et al, 2020; Yasunaga et al, 2017; Xu et al, 2020a通过将边视为连通性来忽略边和节点类型。
   • Cui et al(2020a)将节点投影到统一的嵌入空间，以减少异质性。
   • 一些经典的GNN，如GCN（Xu et al, 2020a; LeClair et al, 2020; Yasunaga et al, 2017）、GAT（Cui et al 2022a）。例如，Fernandes et al(2019)使用关系GGNN来学习节点之间的类型特定关系。Wang et al(2020b)；
   • Jia et al(2020)首先根据节点的类型将异质图拆分为两个子图（即单词图和句子图），然后在两个子图上应用基于GAT的交叉关注来迭代学习表示。
3. **嵌入初始化：**初始节点嵌入的质量对基于GNN的方法的整体性能起着重要作用。
   • 对于节点为单词的图，大多数方法采用预训练的单词嵌入，如BERT (Li et al., 2020c; Xu et al., 2020a; Cui et al., 2020a)、ALBERT（Jiaet al 2020）。
   • 主题图（Cui et al 2020a）引入了额外的主题节点，他们通过主题建模的潜在表示来初始化主题节点。
   • Jin et al(2020b)应用Transformer学习上下文级节点嵌入。
   • 句子节点，Yasunaga et al(2017)采用GRU从相应的单词序列中学习句子嵌入（即节点嵌入）。采用最后隐藏状态作为句子的表示。
   • Wang et al(2020b)采用CNN来捕获细粒度的n元特征，然后使用Bi-LSTM来获得句子的特征向量。
   • Jia et al(2020)将平均池函数应用于ALBERT的编码器输出以表示句子节点
   • Zhao et al(2020c)通过CNN初始化话语节点，通过LDA初始化主题词。

7.1.3 结构化数据到文本

尽管是自然文本，但许多NLP应用都是以明确的图结构来表示数据，如SQL查询、知识图、AMR等。结构化数据的任务就是要从结构化数据输入中生成自然语言。传统的工作应用线性化机制，将结构数据映射为序列数据，并采用Seq2Seq架构来生成文本。为了充分捕捉丰富的结构信息，最近的研究集中在基于GNN的技术来处理这一任务。
大多数基于GNN的AMR-to-text和SQL-to-text方法通常构建特定领域的图，如AMR图和基于SQL解析的图来组织输入。之后，应用由GNN编码器和序列解码器组成的Graph2Seq来生成神经语言输出。

7.1.4 自然问题生成

自然问题生成（QG）任务旨在从某种形式的数据中生成自然语言问题，如KG、表格、文本或图像，其中生成的问题需要从输入数据中得到答案。大多数先前的工作采用了Seq2Seq架构，将输入数据视为序列数据，而不考虑其丰富的结构信息。例如，在对输入文本进行编码时，以前的大多数方法通常会忽略与单词序列相关的隐藏结构信息，如依赖性解析树。即使对于来自KG的QG的设置，大多数方法通常将KB子图线性化为一个序列，并应用一个序列编码器。未能利用输入数据的图结构可能会限制QG模型的有效性。对于在多个段落或文档上进行推理的来自文本的多跳QG，捕捉多个段落或文档中不同实体提及的关系是有益的。总之，**对输入数据的丰富结构进行建模对许多QG任务来说是很重要的。**最近，GNN已经成功应用于QG任务（Liu et al., 2019b; Chen et al., 2020f; Wang et al., 2020c）。
大多数基于GNN的QG方法采用Graph2Seq架构，其中基于GNN的编码器用来对图结构的输入数据进行建模，序列解码器被用来生成自然语言问题。

7.2 机器阅读理解和问题回答

7.2.1 机器阅读理解

机器阅读理解（MRC）的任务旨在利用给定的段落回答一个自然语言问题。由于各种注意力机制的发展，MRC任务已经取得了重大进展，这些机制可以捕捉到问题和上下文之间的相互联系。考虑到传统的MRC设置主要集中在相对简单的一跳推理上，最近，更多的研究工作被用于解决更具挑战性的MRC设置。例如，多跳MRC任务是使用多个段落或文档来回答一个自然语言问题，这需要多跳推理能力。Con- versational MRC任务是在对话中回答当前的自然语言问题，并给出一段话和之前的问题和答案，这需要对对话历史进行建模的能力。数字性的MRC任务要求有对段落进行数字推理的能力。这些具有挑战性的MRC任务需要对对象之间的复杂关系进行建模的学习能力。例如，在多跳MRC任务中，对多个文档之间的关系以及文档中提到的实体进行建模是非常有益的。最近，GNN已经成功应用于各种类型的MRC任务，包括多跳MRC，对话式MRC，以及numerical MRC。
基于GNN的MRC方法通常是通过首先构建一个实体图或层次图来捕捉图中节点之间的丰富关系，然后应用基于GNN的推理模块对图进行复杂推理。假设GNN的输出已经编码了节点本身及其邻居结构的语义，最后将应用一个预测模块来预测答案。为解决MRC任务而开发的图构建技术和图表示技术在不同的方法中有所不同。

7.2.2 知识库问题回答

在过去的几年里，知识库问题回答（KBQA）已经成为一个重要的研究课题。KBQA的目标是给定自然语言问题自动从KG中找到答案。最近，由于其对对象之间关系建模的性质能力，GNN已经成功地应用于执行多跳KBQA任务，这需要对KG的多条边进行推理以得出正确的答案。一个相关的任务是开放领域的QA，其目的是通过利用包括语料库和KG的混合知识源来回答开放领域的问题。本文介绍并总结了最近KBQA研究中采用的一些有代表性的GNN相关技术。

7.2.3 开放域的问题回答

开放域问题回答的任务旨在给定一个大规模的开放域知识（如文档、知识库等），以确定自然问题的答案。基于知识的方法得益于通过图结构轻松获得外部知识。然而，这些方法在知识库和固定模式的信息缺失方面受到限制。为了回答来自海量和非结构化文档的问题，与基于知识库的方法相比，这些方法可以获取更多的信息，但在从冗余的外部文档中检索相关和关键信息方面存在困难。本文介绍并总结了最近开放域问题回答研究中一些有代表性的GNN相关技术。

7.2.4 社区问题回答

社区问题回答的任务旨在从QA论坛（如Stack Overflow或Quora）中检索出相关答案。与传统的MRC（QA）任务不同，CQA系统能够利用隐性知识（嵌入在不同的社区中）或显性知识（嵌入在所有解决的问题中）来回答每天发布的大量新问题。然而，越来越多的新问题可能会使没有适当协作支持的CQA系统因用户的要求而变得超负荷。本文介绍并总结了最近CQA研究中采用的一些有代表性的GNN相关技术。

7.3 对话系统

对话系统是一个可以连续与人对话的计算机系统。为了建立一个成功的对话系统，对对话中不同对话者或话语之间的依赖关系进行建模很重要。由于能够对对象之间的复杂关系进行建模，最近，GNN已经成功地应用于各种对话系统相关的任务，包括对话状态跟踪，旨在估计给定对话历史的当前对话状态；对话响应生成，旨在给定对话历史生成对话响应；以及下一个话语选择，旨在给定对话历史从候选列表中选择下一个话语。本文介绍并总结了近期对话系统研究中采用的一些有代表性的GNN相关技术。

7.4 文本分类

传统的文本分类方法严重依赖特征工程（如BOW、TF-IDF或更高级的基于图形路径的特征）进行文本表示。为了从数据中自动学习 "好的 "文本表征，人们提出了各种无监督的方法来学习单词或文档表征，包括word2vec、GloVe、话题模型、自动编码器和doc2vec。这些预训练的单词或文档嵌入可以进一步被MLP、CNN或LSTM模块所消耗，用于训练监督下的文本分类器。为了更好地捕捉文本或语料库中文件之间的关系，人们提出了各种基于图的方法进行文本分类。例如，Peng等人（2018）提出首先构建一个词的图，然后将CNN应用于规范化的子图。Tang等人提出了一种基于网络嵌入的方法，通过将部分标记的文本语料转换为异质文本网络，以半监督的方式进行文本表示学习。最近，考虑到强大的表达能力，GNN已经成功应用于半监督和监督文本分类中。
基于GNN的文本分类方法通常是，首先构建一个文档图或语料库图来捕捉图中节点之间的丰富关系，然后应用GNN来学习良好的文档嵌入，这些嵌入随后将被送入softmax层以产生一类标签的概率分布。为解决文本分类任务而开发的图构建技术和图表示技术在不同的方法中有所不同。本文介绍并总结了最近的文本分类方法中采用的一些代表性的GNN相关技术。

7.5 文本匹配

现有的大多数文本匹配方法是通过一些神经网络，如CNN或RNN，将每个文本映射到一个潜在的嵌入空间，然后根据文本表征之间的相似性计算匹配分数。为了在不同的颗粒度水平上对两个文本之间的丰富互动进行建模，通常会精心设计复杂的注意力或匹配组件。最近，有一些工作成功地探索了GNNs在文本匹配中对文本元素之间复杂的交互作用进行建模的问题。本文介绍并总结了近期文本匹配方法中采用的一些有代表性的GNN相关技术。

7.6 话题建模

话题建模的任务旨在发现语料库中出现的抽象的 “话题”。通常情况下，话题模型学习将一段文本表示为一个话题的混合物，而话题本身则表示为词汇的混合物。经典的话题模型包括基于图模型的方法，基于自回归模型的方法，以及基于自动编码器的方法。最近的工作通过明确地对文档和词之间的关系进行建模，探索了基于GNN的方法进行话题建模。本文介绍并总结了近期话题建模方法中采用的一些有代表性的GNN相关技术。

7.7 情感分析

情感分析任务旨在检测一段文本的情感（即积极、消极或中立）。方面级的情感分类旨在识别文本在特定方面的情感极性，并受到更多关注。虽然大多数工作都集中在句子层面和单一领域的情感分类上，但在文档层面和跨领域的情感分类上也有一些尝试。早期的情感分类工作主要依赖于特征工程。最近的尝试利用了各种神经网络模型的表达能力，如LSTM、CNN或记忆网络。最近，人们尝试利用GNN来更好地模拟文本的句法和语义，以完成情感分类任务。
基于GNN的情感分类方法通常是通过首先构建文本的图表示（如依赖树），然后应用GNN来学习良好的文本嵌入，这些嵌入将被用于预测情感的极性。为解决情感分类任务而开发的图构建技术和图表示技术在不同的方法中有所不同。本文将介绍并总结最近的情感分类方法中采用的一些有代表性的GNN相关技术。

7.8 知识图谱

知识图谱（KG）以结构化的形式表示现实世界的知识，在学术界和工业界引起了很大的关注。KG可以表示为一组三元组集合。在KG方面有三个主要任务，即知识图谱嵌入(KGE)，知识图谱对齐(KGA)，知识图谱补全(KGC)。本文将对基于图的KGC和KGA方法进行概述。

7.9 信息抽取

信息抽取（IE）的目的是提取给定句子或文档的实体对及其关系。IE是一项重要的任务，因为它有助于从非结构化文本中自动构建知识图谱。随着深度神经网络的成功，基于神经网络的方法已被应用于信息提取。然而，这些方法往往忽略了输入文本的非局部和非序列化的上下文信息。此外，重叠关系的预测，即共享相同实体的一对实体的关系预测，也不能得到妥善解决。为了这些目的，GNN已经被广泛用于建立文本中实体和关系之间的交互模型。信息提取由两个子任务组成：命名实体识别（NER）和关系提取（RE）。NER为句子中的每个词预测一个标签，这通常被认为是一个序列标注任务。RE为文本中的每一对实体预测一个关系类型。当输入文本中的实体被注释后，IE任务就退化为RE任务。基于GNN的IE方法通常通过pipeline的方式运作。首先，构建一个文本图。然后，实体被识别，实体对之间的关系被预测。本文是对基于GNN的不同技术的介绍。

7.10 语义语法解析

在本节中主要讨论GNN在解析方面的应用，包括与语法相关的解析和与语义相关的解析。对于语法相关的解析，GNN已经被用于依赖性解析和成分解析的任务。对于语义相关的解析，本文简要介绍语义解析和AMR解析。

7.11 推理

推理是NLP的一个重要研究方向。近年来，GNN开始在NLP推理任务中发挥重要作用，如数学单词问题解决，自然语言推理，常识推理等。本文将对这三个任务以及GNN在这些方法中的应用做一个简要介绍。

7.12 语义角色标注

语义角色标注（SRL）问题旨在恢复一个句子的predicate-argument结构，即基本上确定 “谁对谁做了什么”、"何时 "和 “何地”。对于每个谓词，SRL模型必须识别所有的argument跨度，并为它们标注语义角色。这样的高层结构可以作为语义信息，用于支持各种下游任务，包括对话系统、机器阅读和翻译。最近的SRL工作大多可以分为两类，即根据是否纳入句法知识，分为句法感知型和句法诊断型方法。大多数syntax-agnostic的工作采用深度BiLSTM或自注意编码器来编码自然句子的上下文信息，用各种评分器来预测基于BIO的语义角色的概率或predicate-argument-role元组。在句法和语义之间强烈的相互作用的激励下，研究人员探索了各种方法，将句法知识整合到句法无关的模型中，考虑到语义表示与句法表示密切相关。例如，我们可以观察到，句法依赖图中的许多弧在语义依赖图中都有反映。鉴于这些相似性以及许多语言都有精确的句法分析器，在预测语义时利用句法信息似乎是很自然的。
采用神经序列模型，即LSTM，存在以下挑战：（1）由于句法关系的复杂树状结构，很难有效地将句法信息纳入神经SRL模型；（2）由于错误的句法输入的风险，句法分析器是不可靠的，这可能导致错误传播和不理想的SRL性能。鉴于这种情况，GNN正在成为捕捉和纳入基于深度神经网络的SRL模型中的语法模式的有力工具。在捕捉结构化数据中的复杂关系模式方面，GNN的性质使其很适合于为句子的句法依赖和成分结构建模。
从形式上看，SRL可以被投射为一个序列标注问题，即给定一个输入句子，以及谓词在句子中的位置，目标是预测句子中的词的语义角色的BIO序列；另一个是关于端到端的语义角色三元组提取，目的是一次性检测所有可能的谓词和它们相应的arguments。从技术上讲，给定一个句子，SRL模型会预测一组标记的谓语-参数-角色三元组，而每个三元组包含一个可能的谓语标记和两个候选标记。上述两个问题都可以基于基于GNN的SRL模型来解决，它由两部分组成，即图的构建和图的表示学习。

8. 结论

本文对各种GNN演化出的各种NLP问题进行了全面的概述。具体来说，首先提供了典型的GNN模型的初步知识，包括图过滤器和图池化方法。然后提出了一个新的分类法，沿着三个维度系统地组织GNNs for NLP方法，即图的构造、图表示学习和编码器-解码器模型。鉴于这些在NLP应用每个阶段的具体技术，从图构建、图表示学习和具体技术的角度讨论了大量的NLP应用。最后为进一步释放GNN在NLP领域的巨大潜力，本文提供了这一思路的大体挑战和未来方向。