动态规划算法---钢条切割

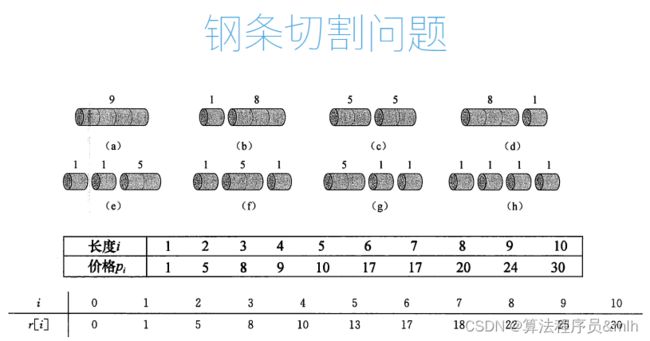
钢条切割问题：

程序实现：

方法一和方法二是对程序实现的不断深入，逐渐降低算法实现的时间复杂度。

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]
# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
#方法一，两边都切割，重复了很多计算
#@cal_time
def cut_rod_recurision_1(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in (1, n):
            res = max(res, cut_rod_recurision_1(p, i) + cut_rod_recurision_1(p, n-i))
        return res
#方法二，左边不切割，只切割右边，减少了很多重复计算
def cut_rod_recurision_2(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1, n+1):#此处是1到n+1，即i为1到n
            res = max(res, p[i] + cut_rod_recurision_1(p, n - i))
        return res
#方法一、二都是自顶向下的思想，先算r[10],r[10]为r[2]+r[8],然后r[2]和r[8]不断递归。

方法三，动态规划—自底向上，结果最优（所需时间最短）

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]
# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]

#方法三，自底向上的思想，也就是动态规划的思想
def cut_rod_dp(p, n):
    r = [0]
    for i in range(1, n+1):
        res = 0
        for j in range(1, i+1):
            res = max(res, p[j] + cut_rod_dp(p, i-j))
            # res = max(res, p[j] + r[i-j])
        r.append(res)
        # r[i] = res
    return r[n]

算法完整程序：

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]
# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]

#情况五、进阶返回切割好的情况
def cut_rod_extend(p, n):
    r = [0]
    s = [0]
    for i in range(1, n+1):
        res_r = 0 #表示价格的最大值
        res_s = 0 #价格最大值对应方案的左边不切割的长度
        for j in range(1, i+1):
            if res_r < p[j] + r[i-j]:
                res_r = p[j] + r[i-j]
                res_s = j
        r.append(res_r)
        s.append(res_s)
    return r[n],s

def cut_rod_solution(p, n):
    r,s = cut_rod_extend(p, n)
    ans = []
    while n > 0:
        ans.append(s[n])
        n -= s[n]
    return ans


print(cut_rod_solution(p,20))