图像算法四 —— 线性SVM算法 及 非线性SVM算法

4. 线性SVM算法 及 非线性SVM算法

SVM 简介

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是：定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。

SVM还包含核技巧，这使它成为实质上的非线性分类器。

SVM的学习策略就是——间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数最小化问题。

SVM的学习算法，就是求解凸二次规划的最优化算法。

SVM的优缺点

优点

1. 非线性映射是SVM方法的理论基础，SVM利用内积核函数代替向高维空间的非线性映射；

2. 对特征空间划分的最优超平面是SVM的目标，最大化分类边际的思想是SVM方法的核心；

3. 支持向量是SVM的训练结果，在SVM分类决策中起决定作用的是支持向量。

4. SVM 是一种有坚实理论基础的新颖的小样本学习方法。它基本上不涉及概率测度及大数定律等，因此不同于现有的统计方法。从本质上看,它避开了从归纳到演绎的传统过程，实现了高效的从训练样本到预报样本的“转导推理”，大大简化了通常的分类和回归等问题。

5. SVM 的最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了维数灾难。

6. 少数支持向量决定了最终结果,这不但可以帮助我们抓住关键样本、“剔除”大量冗余样本,而且注定了该方法不但算法简单,而且具有较好的鲁棒性。这种“鲁棒”性主要体现在:

   • ① 增、删非支持向量样本对模型没有影响;

   • ② 支持向量样本集具有一定的鲁棒性;

   • ③ 有些成功的应用中,SVM 方法对核的选取不敏感

缺点

• SVM算法对大规模训练样本难以实施

由于SVM是借助二次规划来求解支持向量，而求解二次规划将涉及m阶矩阵的计算（m为样本的个数），当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对以上问题的主要改进有有J.Platt的SMO算法、T.Joachims的SVM、C.J.C.Burges等的PCGC、张学工的CSVM以及O.L.Mangasarian等的SOR算法

• 用SVM解决多分类问题存在困难

经典的支持向量机算法只给出了二类分类的算法，而在数据挖掘的实际应用中，一般要解决多类的分类问题。可以通过多个二类支持向量机的组合来解决。主要有一对多组合模式、一对一组合模式和SVM决策树；再就是通过构造多个分类器的组合来解决。主要原理是克服SVM固有的缺点，结合其他算法的优势，解决多类问题的分类精度。如：与粗集理论结合，形成一种优势互补的多类问题的组合分类器。

线性SVM算法原理

原理解释

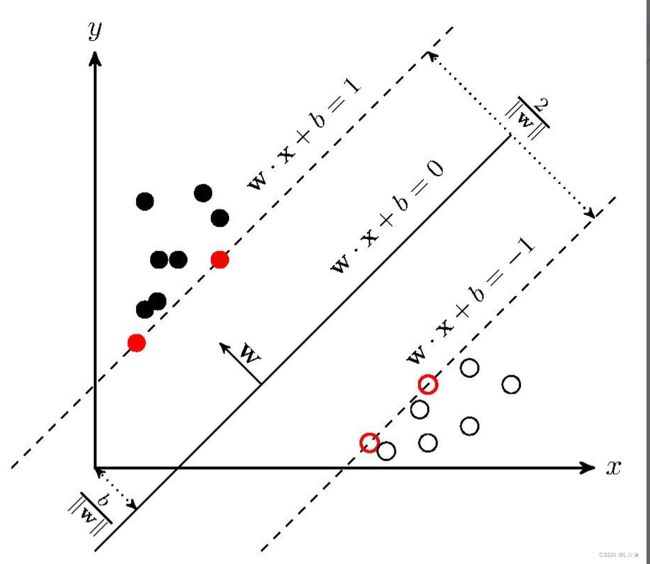
SVM学习的基本想法是，求解能够正确划分训练数据集，并且几何间隔最大的 分离超平面。如下图所示，$w\cdot x+b=0$即为分离超平面。对于线性可分的数据集来说，这样的超平面有无穷多个（即 感知机），但是几何间隔最大的分离超平面 是唯一的。

原理推导

​ 假设给定 一个特征空间上的训练数据集

$$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$$

其中，

$x_i \in \mathbb{R}^n $，

$y_i\in \{+1,-1\},i=1,2,\cdots ,N$，

$x_i$为第$i$个特征向量

$y_i$为类标记。$i=+1$时，为正例；$i=-1$时，为负例。

再假设训练数据集是 线性可分的。

几何间隔：对于给定的数据集$T$和超平面$w\cdot x+b=0$，定义超平面关于样本点$(x_i,y_i)$的几何间隔为：

$${\gamma }_i=y_i(\frac{w}{||w||}\cdot x_i+\frac{b}{||w||})$$

超平面关于所有样本点的几何间隔的最小值为：

$$\gamma =\underset{i=1,2,\cdots ,N}{\min }{\gamma }_i$$

这个距离就是 我们所谓的支持向量到超平面的距离。

$①$ 根据以上定义，SVM模型的求解最大分割超平面问题可以表示为以下的约束最优化问题：

$$\underset{w,b}{\max }\gamma$$

$$s.t.y_i(\frac{w}{||w||}\cdot x_i+\frac{b}{||w||})\ge \gamma ,i=1,2,\cdots ,N$$

$②$ 将约束条件两边，同时除以$\gamma$，得到：

$$y_i(\frac{w}{||w||\gamma }\cdot x_i+\frac{b}{||w||\gamma })\ge 1$$

$③$ 因为$||w||$，$\gamma$都是标量，所以为了表达式简洁起见，令

$w=\frac{w}{||w||\gamma }$

$b=\frac{b}{||b||\gamma }$

得到：

$$y_i(w\cdot x_i+b)\ge 1,i=1,2,\cdots ,N$$

$④$ 又因为最大化$\gamma$，等价于最大化$\frac{1}{||w||}$，也就是等价于最小化$\frac{1}{2}||w|{|}^2$（$\frac{1}{2}$是为了后面求导以后形式简洁，不影响结果），因此SVM模型的求解最大分割超平面问题，又可以表示为以下约束最优化问题：

$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$$

$$s.t.y_i(w\cdot x_i+b)\ge 1,i=1,2,\cdots ,N$$

​ 这是一个含有不等式约束的凸二次规划问题，可以对其使用拉格朗日乘子法，得到其对偶问题(dual problem)。

$⑤$ 首先，我们将有约束的原始目标函数，转换为，无约束的新构造的 拉格朗日目标函数

$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^N{\alpha }_i(y_i(w\cdot x_i+b)-1)$$

其中，

${\alpha }_i$——拉格朗日乘子，且${\alpha }_i\ge 0$.

$⑥$ 现在，我们令

$$\theta (w)=\underset{{\alpha }_i\ge 0}{\max }L(w,b,\alpha )$$

• 当样本点不满足约束条件时，即在可行解区域外：

$$y_i(w\cdot x_i+b)<1$$

​ 此时，将$\alpha$设置为无穷大，则$\theta (w)$也为无穷大。

• 当样本点满足约束条件时，即在可行解区域内：

$$y_i(w\cdot x_i+b)\ge 1$$

​ 此时，$\theta (w)$为原函数本身。

$⑦$ 于是，将这两种合并，得到新的目标函数为：

$$\theta (w)=\{\begin{array}{ll}\frac{1}{2}||w|{|}^2& x\in \text{可行区域}\\ +\infty & x\in \text{不可行区域}\end{array}$$

于是，原约束问题就等价于

$$\underset{w,b}{\min }\theta (w)=\underset{w,b}{\min }\underset{a_i\ge 0}{\max }L(w,b,\alpha )=p^{\ast }$$

$⑧$ 看一下我们的新目标函数，先求最大值，再求最小值。这样的话，我们首先就要面对带有需要求解的参数$w$和$b$的方程，而${\alpha }_i$又是不等式的约束，这个求解过程不好做。

​ 所以，我们需要用拉格朗日对偶性，将最小和最大的位置交换一下，这样就变成了：

$$\underset{w,b}{\min }\theta (w)=\underset{a_i\ge 0}{\max }\underset{w,b}{\min }L(w,b,\alpha )=d^{\ast }$$

$⑨$ 要有$p^{\ast }=d^{\ast }$，需要满足两个条件：

• 优化问题是凸优化问题

• 满足KKT条件

  首先，优化问题显然是一个凸优化问题，所以条件一满足。

  条件二，即要求

  $$\{\begin{array}{l}{\alpha }_i\ge 0\\ y_i(w_i\cdot x_i+b)-1\ge 0\\ {\alpha }_i(y_i(w_i\cdot x_i+b)-1)=0\end{array}$$

$⑩$ 为求解对偶问题的具体形式，令$L(w,b,\alpha )$对$w$和$b$的偏导为0，可得

$$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$

$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$

$⑪$ 将以上两个等式，带入拉格朗日目标函数，消去$w$和$b$，得到：
$$\begin{array}{rl}L(w,b,\alpha )& =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i{y}_i((\sum _{j=1}^N{\alpha }_j{y}_j{x}_j)\cdot x_i+b)+\sum _{i=1}^N{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i\end{array}$$
即：

$$\underset{w,b}{\min }L(w,b,\alpha )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i$$

$⑫$ 求 ${\min }_{w,b}L(w,b,\alpha )$对$\alpha$的 极大，即是 对偶问题：

$$\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i$$

$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$

$${\alpha }_i\ge 0,i=1,2,\cdots ,N$$

把目标式子加一个负号，将求极大转换为求极小。

$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i$$

$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$

$${\alpha }_i\ge 0,i=1,2,\cdots ,N$$

$⑬$ 这里我们的优化问题变成了如上的形式，对于这个问题，我们还有更高效的优化算法，即序列最小优化（SMO）算法。用到的不多，不详细了解，有需要请自行了解。

​ 我们通过SMO算法，可以得到${\alpha }^{\ast }$ ，再根据${\alpha }^{\ast }$，我们就可以求解出$w$和$b$，进而求得我们最初的目的：找到超平面，即“决策面”

$⑭$ 前面的推导都是假设满足KKT条件下成立的，KKT条件如下：

$$\{\begin{array}{l}{\alpha }_i\ge 0\\ y_i(w_i\cdot x_i+b)-1\ge 0\\ {\alpha }_i(y_i(w_i\cdot x_i+b)-1)=0\end{array}$$

此外，根据前面的推导，还有下面两个式子成立：

$$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$

$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$

$⑮$ 由此可知，在${\alpha }^{\ast }$中，至少存在一个${\alpha }_j^{\ast }>0$（反证法可以证明，若全为0，则$w=0$，矛盾），

对此$j$有

$$y_j(w^{\ast }\cdot x_j+b^{\ast })-1=0$$

$⑯$ 因此可以得到

$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$

$$b^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$$

对于任意训练样本$(x_i,y_i)$，总有${\alpha }_i=0$，或者$y_i(w\cdot x_j+b)=1$。

• 若${\alpha }_i=0$，则该样本不会在最后求解模型参数的式子中出现。

• 若${\alpha }_i>0$，则必有$y_i(w\cdot x_j+b)=1$，所对应的样本点位于最大间隔边界上，是一个支持向量。

  这显示出支持向量机的一个重要性质：训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

$⑰$ 到这里，都是基于训练集数据线性可分的假设下进行的，但是实际情况下，几乎不存在完全线性可分的数据，为了解决这个问题，引入了“软间隔”的概念，即允许某些点不满足约束。

$$y_j(w\cdot x_j+b)\ge 1$$

采用hinge损失，将原优化问题改写为：

$$\underset{w,b,{\xi }_i}{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i$$

$$s.t.y_i(w\cdot x_i+b)\ge 1-{\xi }_i$$

$${\xi }_i\ge 0,i=1,2,\cdots ,N$$

其中，

${\xi }_i$——“松弛变量”，每一个样本都有一个对应的松弛变量，用来表征该样本不满足约束的程度。

${\xi }_i=\max (0,1-y_i(w\cdot x_i+b))$，即一个hinge损失函数。

$C>0$——惩罚参数。$C$值越大，对分类的惩罚越大。

同线性可分求解的思路一致，同样这里也是先用拉格朗日乘子法得到拉格朗日函数，再求对偶问题。

线性支持向量机的学习算法

输入： 训练数据集 $T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$， 其中 $x_i\in {\mathbb{R}}^n$，$y_i\in \{+1,-1\},i=1,2,\cdots ,N$

输出： 分离超平面和分类决策函数

（1） 选择惩罚参数$C>0$，构造并求解凸二次规划文题

$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i$$

$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$

$$0\le {\alpha }_i\le C,i=1,2,\cdots ,N$$

得到最优解：

$${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }{)}^T$$

（2） 计算

$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$

选择${\alpha }^{\ast }$的一个分量${\alpha }_j^{\ast }$满足条件$0<{\alpha }_j^{\ast }<C$，计算

$$b^{\ast }=y_i-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$$

（3） 求分离超平面

$$w^{\ast }\cdot x+b^{\ast }=0$$

分类决策函数：

$$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$$

非线性SVM算法原理

非线性支持向量机的求解

对于输入空间中的非线性分类问题，可以通过非线性变换将它转换为某个维特征空间中的线性分类问题，在高维特征空间中学习线性支持向量机。

由于在线性支持向量机学习的对偶问题里，目标函数和分类决策函数都只涉及实例和实例之间的内积，所以不需要显式地指定非线性变换，而是用核函数替换当中的内积。

核函数表示，通过一个非线性转换后的两个实例之间的内积。

具体地，$K(x,z)$是一个函数，或正定核，意味着存在一个从输入空间到特征空间的映射$\varphi (x)$，对任意输入空间中的$x,z$，有：

$$K(x,z)=\varphi (x)\cdot \varphi (z)$$

在线性支持向量机学习的对偶问题中，用核函数$K(x,z)$替代内积，求解得到的就是非线性支持向量机：

$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x,x_i)+b^{\ast })$$

非线性支持向量机学习算法

输入： 训练数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$， 其中$x_i\in {\mathbb{R}}^n$，$y_i\in \{+1,-1\},i=1,2,\cdots ,N$

输出： 分离超平面和分类决策函数

（1） 选择适当的核函数$K(x,z)$和惩罚参数$C>0$，构造并求解凸二次规划文题

$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i$$

$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$

$$0\le {\alpha }_i\le C,i=1,2,\cdots ,N$$

得到最优解：

$${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }{)}^T$$

（2） 选择${\alpha }^{\ast }$的一个分量${\alpha }_j^{\ast }$满足条件$0<{\alpha }_j^{\ast }<C$，计算

$$b^{\ast }=y_i-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i\cdot x_j)$$

（3） 分类决策函数：

$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x,x_i)+b^{\ast })$$

常用核函数——高斯核函数

高斯核函数为一个常用的核函数，其公式如下：

$$K(x,z)=exp(-\frac{||x-z|{|}^2}{2{\sigma }^2})$$

对应的SVM是高斯径向基函数分类器，在此情况下，分类决策函数为：

$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}exp(-\frac{||x-z|{|}^2}{2{\sigma }^2})+b^{\ast })$$