数学建模之TOPSIS法
目录
问题
引入
问题实例
问题分析
模型建立
统一指标类型
进行标准化
计算结果
拓展
四种指标及其正向化
标准化
计算结果
解决问题实例
问题
函数介绍
代码介绍
结果验证
总结与注意
问题
引入
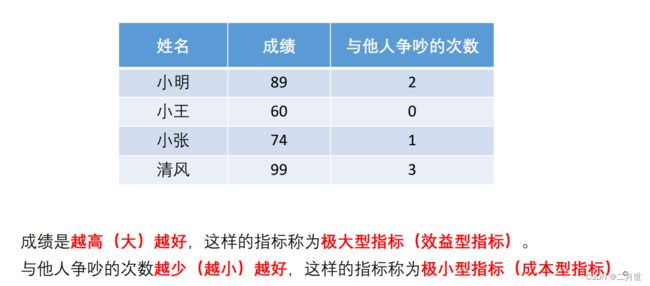
问题实例
问题分析
几点解释,为什么不用100和0来代表MAX和MIN
以上是一个简单的问题使用TOPSIS初步分析
模型建立
在上述问题拓展一下
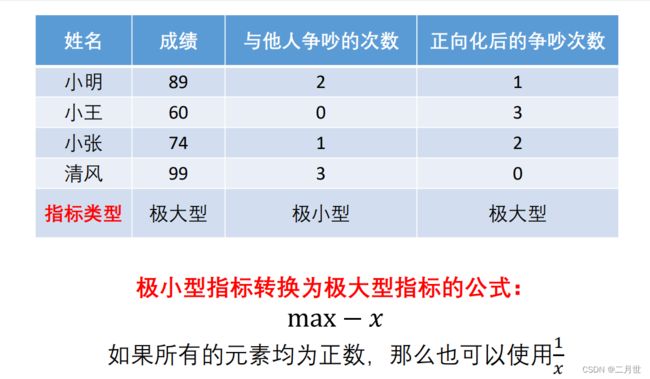
统一指标类型
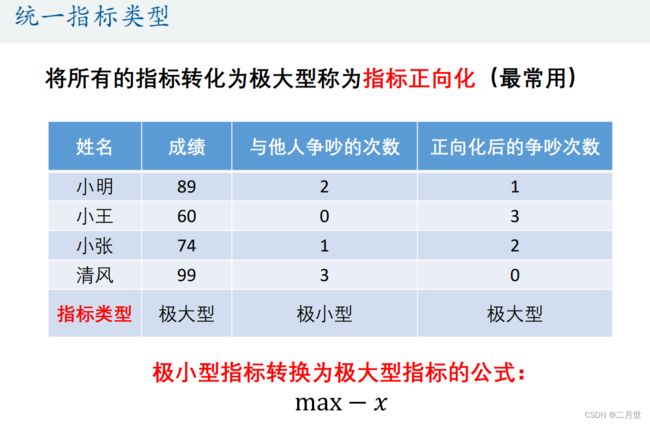 进行标准化
进行标准化
计算结果
拓展
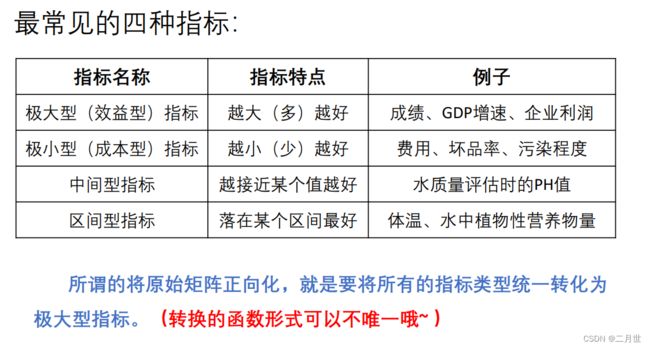
四种指标及其正向化
中间型转极大型
区间型转极大型
标准化
计算结果
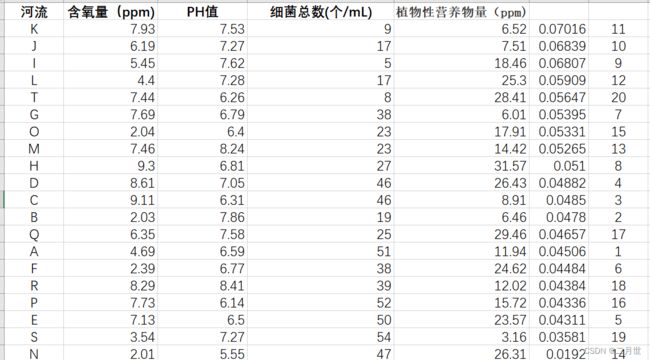
解决问题实例
问题
函数介绍
%保存并加载excel数据,保存为.mat文件
clear;clc
load data_water_quality.mat
%幻方矩阵
A = magic(5) % 幻方矩阵
M = magic(n) %返回由1到n^2的整数构成并且总行数和总列数相等的n×n矩阵。
%阶次n必须为大于或等于3的标量。
%排序函数sort
% sort(A)若A是向量不管是列还是行向量,默认都是对A进行升序排列。sort(A)是默认的升序,而sort(A,'descend')是降序排序。
% sort(A)若A是矩阵,默认对A的各列进行升序排列
% sort(A,dim)
% dim=1时等效sort(A) % dim=2时表示对A中的各行元素升序排列
% Matlab中给一维向量排序是使用sort函数:sort(A),排序是按升序进行的,其中A为待排序的向量;
% 若欲保留排列前的索引,则可用 [sA,index] = sort(A,'descend') ,排序后,sA是排序好的向量,index是向量sA中对A的索引。
%关于使用函数
%自定义的函数不可以与主函数在一个文件,一般一个函数为一个文件(与主函数同为.m),放在同一目录下调用代码介绍
主函数
clear;clc
load Data.mat
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象,' num2str(m) '个评价指标']);
judge = input(['这' num2str(m) '个指标,是否需要进行正向化处理(需要请输入1,不需要请输入0):']);
if judge == 1
position = input('请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]: '); %[2,3,4]
disp('请输入需要处理的这些列的指标类型(1:极小型, 2:中间型, 3:区间型) ');
type = input('例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]: ');
for i = 1 : size(position,2)
X(:,position(i)) = Positivization(X(:,position(i)),type(i),position(i));
end
disp('正向化后的矩阵X = ');
disp(X);
end
Z = X ./ repmat(sum(X.*X) .^ 0.5,n,1);
disp('标准化矩阵 Z = ');
disp(Z);
D_P = sum((Z - repmat(max(Z),n,1)) .^ 2 ,2) .^ 0.5;
D_N = sum((Z - repmat(min(Z),n,1)) .^ 2 ,2) .^ 0.5;
S = D_N ./ (D_P + D_N);
stand_S = S/sum(S)
[sorted_S,index] = sort(stand_S ,'descend')调用函数
function [posit_X] = Positivization(X,type,i)
if type == 1
disp(['第' num2str(i) '列是极小型,正在正向化']);
posit_X = Min2Max(X); %调用Min2Max函数来正向化
disp(['第' num2str(i) '列极小型正向化处理完成'] );
disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~');
elseif type == 2
disp(['第' num2str(i) '列是中间型,正在正向化']);
best = input('请输入最佳的那一个值: ');
posit_X = Mid2Max(X,best); %调用Mid2Max函数来正向化
disp(['第' num2str(i) '列中间型正向化处理完成'] );
disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~');
elseif type == 3
disp(['第' num2str(i) '列是区间型,正在正向化']);
a = input('请输入区间的下界: ');
b = input('请输入区间的上界: ');
posit_X = Inter2Max(X,a,b); %调用Inter2Max函数来正向化
disp(['第' num2str(i) '列区间型正向化处理完成'] );
disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
else
disp('没有这种类型的指标,请检查Type向量中是否有除了1、2、3之外的其他值');
end
end
function [posit_X] = Min2Max(X)
posit_X = max(X)-X;
end
function [posit_X] = Mid2Max(X,best)
M = max(abs(X-best));
posit_X = 1-abs(X-best)/M;
end
function [posit_X] = Inter2Max(X,a,b)
r_x = size(X,1);
M = max(a-min(X),max(X)-b);
posit_X = zeros(r_x,1); %zeros函数用法: zeros(3) zeros(3,1) ones(3)
% 初始化posit_x全为0 初始化的目的是节省处理时间
for i = 1:r_x
if X(i) < a
posit_X(i) = 1-(a-X(i))/M;
elseif X(i) > b
posit_X(i) = 1 - (X(i)-b)/M;
else
posit_X(i) = 1;
end
end
end与层次分析法的结合
%% 让用户判断是否需要增加权重
disp('请输入是否需要增加权重向量,需要输入1,不需要输入0')
Judge = input('请输入是否需要增加权重: ');
if Judge == 1
disp(['如果你有3个指标,你就需要输入3个权重,例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);
weigh = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);
OK = 0; % 用来判断用户的输入格式是否正确
while OK == 0
if abs(sum(weigh) - 1)<0.000001 && size(weigh,1) == 1 && size(weigh,2) == m % 这里要注意浮点数的运算是不精准的。
OK =1;
else
weigh = input('你输入的有误,请重新输入权重行向量: ');
end
end
else
weigh = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同,即都为1/m
end%% 第四步:计算与最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5; % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5; % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N); % 未归一化的得分
disp('最后的得分为:')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')结果验证
总结与注意
%在导入excel数据时,若在matlab内导入,记得选输出样式为数字矩阵,不然就是table类型,会对下面的计算造成影响。
%也可以直接创建变量修改值,粘贴数据
% for语句起始与终点的链接是:而不是;