魂断蓝桥杯:动态规划
目录
- 前言
- 1. 什么是动态规划
- 2. 利用动规解决问题
-
- 2.1 斐波那契数列
- 2.2 字符串分割
- 2.3 三角矩阵
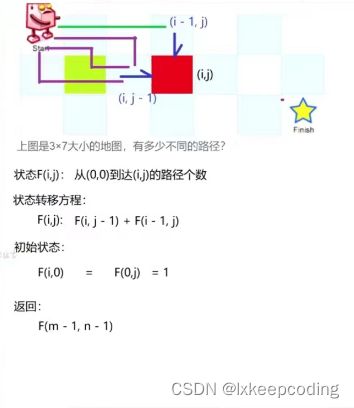
- 2.4 路径总数
- 2.5 最小路径和
- 2.6 背包问题
- 2.7 回文串分割
- 2.8 编辑距离
- 2.9 不同子序列
- 后记
前言
hello,大家好,手欠报了一个蓝桥杯,报完了后悔了,但这玩意贵在参与,于是决定象征性地准备一下,于是开了这个专栏,不知道什么时候就不更啦哈,我向来是三天打鱼两天晒网的哈。
很迷茫,明年这个时候考研考场上就是我了,不知道未来该往哪里去。整个现在的状态就是很颓废。希望能够早点不颓废。
不说了,开始写博客了。祝大家万事胜意。
1. 什么是动态规划
动态规划定义:

动态规划特点:

动态规划问题考虑:

状态定义的要求:一定要形成递推关系
动态规划适用场景:最大值/最小值、可行不可行、是不是、方案个数
2. 利用动规解决问题
2.1 斐波那契数列
class solution
{
public:
int Fobocinacci(int n)
{
//创建一个数组,保存中间状态的解
int *F = new int[n + 1];
//初始化F[0]、F[1]
F[0] = 0;
F[1] = 1;
//F[i]=F[i-1]+F[i-2]
for (int i = 2; i <= n; i++)
{
F[i] = F[i - 1] + F[i - 2];
}
return F[n];
}
};
在这个问题中,时间复杂度为O(n)。只利用了一个循环就解决了问题,这就是动规的魅力。
当然,这个代码在空间复杂度上还有优化的可能。
class solution
{
public:
int Fobocinacci(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
int fn;
int fn1 = 1;
int fn2 = 0;
for (int i = 2; i <= n; i++)
{
fn = fn1 + fn2;
//更新中间状态哦
fn2 = fn1;
fn1 = fn;
}
return fn;
}
};
2.2 字符串分割
public class Solution
{
public boolean wordbreak(String s, Set<String>dict)
{
boolean[] canbreak = new boolean[s.length() + 1];
//初始化
canbreak[0] = true;
for (int i = 1; i <= s.length(); ++i)
{
//j
for (int j = 0; j < i; ++j)
{
if (canbreak[j] && dict.contains(s.substring(j, i)))
{
canbreak[i] = true;
break;
}
}
}
return canbreak[s.length()];
}
};
2.3 三角矩阵
class Solution{
public:
int minimumTotal(vector<vector int> &triangle){
if (triangle.empty())
return 0;
int row = triangle.size();
int col = triangle[0].size();
for (int i = 1; i < row; ++i)
{
for (int j = 0; j <= i; ++j)
{
if (j == 0)
triangle[i][j] = triangle[i - 1][j] + triangle[i][j];
if (j == i)
triangle[i][j] = triangle[i - 1][j - 1] + triangle[i][j];
else
{
triangle[i][j] =min( triangle[i - 1][j - 1] + triangle[i-1][j])+triangle[i][j];
}
}
}
int minSum = triangle[row - 1][0];
for (int j = 1; j < row; ++j)
minSum = min(minSum, triangle[row - 1][j]);
return minSum;
}
};
2.4 路径总数
public class Solution{
public int uniquePaths(int m, int n){
int[][]pathNum = new int[m][n];
for (int i = 0; i < m; ++i)
pathNum[i][0] = 1;
for (int j = 0; j < n; ++j)
pathNum[0][j] = 1;
for (int i = 1; i < m; ++i)
{
for (int j = 0; j < n; ++j)
pathNum[i][j] = path[i][j-1] + path[i - 1][j];
}
return pathNum[m - 1][n - 1];
}
};
2.5 最小路径和
class Solution{
public:
int minPathSum(vector<vector<int>>&grid){
if (grid.size() == 0)
return 0;
int row = grid.size();
int col = grid[0].size();
//第一行
for (int i = 1; i < col; ++i)
grid[0][i] = grid[0][i - 1] + grid[0][1];
//第一列
for (int i = 1; i < col; ++i)
grid[i][0] = grid[i-1][0] + grid[i][0];
for (int i = 1; i < row; ++i)
{
for (int j = 1; j < col; ++j)
{
grid[i][j] = min(grid[i][j - 1], grid[i - 1][j] + grid[i][j]);
}
}
return grid[row - 1][col - 1];
}
};
2.6 背包问题
class Solution {
public:
int backPackII(int m, vector<int> A, vector<int> V) {
if (A.empty() || V.empty() || m < 1) {
return 0;
} /
/ 多加一行一列,用于设置初始条件
const int N = A.size() + 1;
const int M = m + 1;
vector<vector<int> > result;
result.resize(N);
//初始化所有位置为0,第一行和第一列都为0,初始条件
比特就业课for(int i = 0; i != N; ++i) {
result[i].resize(M, 0);
} f
or(int i = 1; i < N; ++i) {
for (int j = 1; j != M; ++j) {
//第i个商品在A中对应的索引为i-1: i从1开始
//如果第i个商品大于j,说明放不下, 所以(i,j)的最大价值和(i-1,j)相同
if (A[i - 1] > j) {
result[i][j] = result[i - 1][j];
} /
/ 如果可以装下,分两种情况,装或者不装
//如果不装,则即为(i-1, j)
//如果装,需要腾出放第i个物品大小的空间: j - A[i-1],装入之后的最大价值即为(i - 1, j
- A[i - 1]) + 第i个商品的价值V[i - 1]
//最后在装与不装中选出最大的价值
else {
int newValue = result[i - 1][j - A[i - 1]] + V[i - 1];
result[i][j] = max(newValue, result[i - 1][j]);
}
}
} /
/ 返回装入前N个商品,物品大小为m的最大价值
return result[N - 1][m];
}
};
2.7 回文串分割
class Solution {
public:
int minCut(string s) {
if (s.empty()) return 0;
int len = s.size();
vector<int> cut;
// F(i)初始化
// F(0)= -1,必要项,如果没有这一项,对于重叠字符串“aaaaa”会产生错误的结果
for (int i = 0; i < 1 + len; ++i) {
cut.push_back(i - 1);
} f
or(int i = 1; i < 1 + len; ++i) {
for (int j = 0; j < i; ++j) {
// F(i) = min{F(i), 1 + F(j)}, where j
// 从最长串判断,如果从第j+1到i为回文字符串
// 则再加一次分割,从1到j,j+1到i的字符就全部分成了回文字符串
if (isPalindrome(s, j, i - 1)) {
cut[i] = min(cut[i], 1 + cut[j]);
}
}
} r
eturn cut[len];
} /
/ 判断是否回文串
bool isPalindrome(string s, int i, int j){
while (i<j) {
if (s[i] != s[j]){
return false;
} i
++;
j--;
} r
eturn true;
}
};
2.8 编辑距离
class Solution {
public:
int minDistance(string word1, string word2) {
// word与空串之间的编辑距离为word的长度
if (word1.empty() || word2.empty()) {
return max(word1.size(), word2.size());
} i
nt len1 = word1.size();
int len2 = word2.size();
// F(i,j)初始化
vector<vector<int> > f(1 + len1, vector<int>(1 + len2, 0));
for (int i = 0; i <= len1; ++i) {
f[i][0] = i;
} f
or(int i = 0; i <= len2; ++i) {
f[0][i] = i;
} f
or(int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
// F(i,j) = min { F(i-1,j)+1, F(i,j-1) +1, F(i-1,j-1) +(w1[i]==w2[j]?0:1) }
// 判断word1的第i个字符是否与word2的第j个字符相等
if (word1[i - 1] == word2[j - 1]) {
f[i][j] = 1 + min(f[i][j - 1], f[i - 1][j]);
// 字符相等,F(i-1,j-1)编辑距离不变
f[i][j] = min(f[i][j], f[i - 1][j - 1]);
} e
lse{
f[i][j] = 1 + min(f[i][j - 1], f[i - 1][j]);
// 字符不相等,F(i-1,j-1)编辑距离 + 1
f[i][j] = min(f[i][j], 1 + f[i - 1][j - 1]);
}
}
} r
eturn f[len1][len2];
}
};
2.9 不同子序列
class Solution {
public:
int numDistinct(string S, string T) {
int s_size = S.size();
int t_size = T.size();
// S的长度小于T长度,不可能含有与T相同的子串
if (S.size() < T.size()) return 0;
// T为空串,只有空串与空串相同,S至少有一个子串,它为空串
if (T.empty()) return 1;
// F(i,j),初始化所有的值为0
vector<vector<int> > f(s_size + 1, vector<int>(t_size + 1, 0));
// 空串与空串相同的个数为1
f[0][0] = 1;
for (int i = 1; i <= s_size; ++i) {
// F(i,0)初始化
f[i][0] = 1;
for (int j = 1; j <= t_size; ++j) {
// S的第i个字符与T的第j个字符相同
if (S[i - 1] == T[j - 1]) {
f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
} e
lse{
// S的第i个字符与T的第j个字符不相同
// 从S的前i-1个字符中找子串,使子串与T的前j个字符相同
f[i][j] = f[i - 1][j];
}
}
} r
eturn f[s_size][t_size];
}
};
后记
这篇就先到这里,写地不是很好,希望以后有机会再完善。