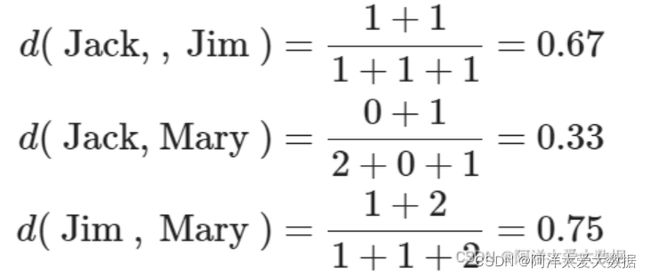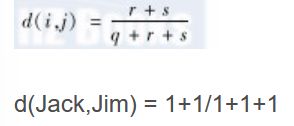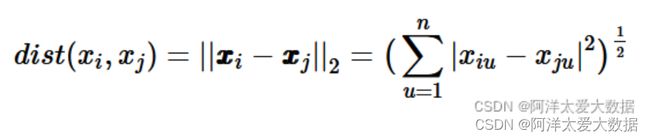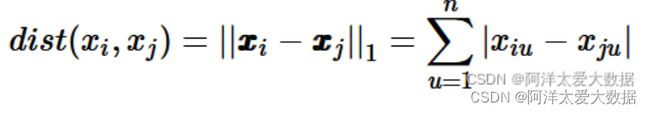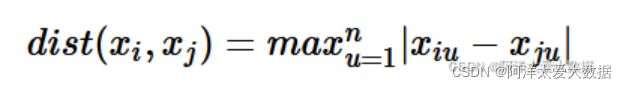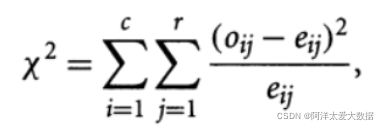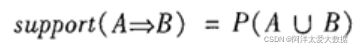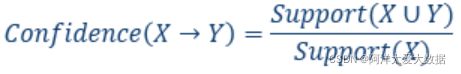数据挖掘部分整理(到关联规则挖掘)
属性类型:
标称属性:值是一些符号或者事务的名称,每个值代表某种类别、编码或者状态,因此标称属性又被看做是分类的,值是无意义的序,并且不是定量的,因此找平均值和中位数是没有意义的,比如:hair_color(头发的颜色)就是。
二元属性:是一种标称属性,只有两个类别状态:0或者1,0通常表示该属性不出现,而1表示出现。二元属性也有对称的二元属性和非对称的二元属性,如果状态的结果不是同等重要的,则称为非对称的二元属性。
- 对称的二元属性
- 非对称的二元属性
序数属性:其可能的值之间具有有意义的量,例如:饮料量的大中小,军衔的等级,成绩的等级,等等。
数值属性:1.区间标度属性:用相等的单位尺度度量(只能差值,不能比率)
2.比率标度属性:属性是具有固有零点的数据属性。(可以比率)
数据的基本统计描述
1.中心趋势度量:度量数据分布的中部或中心位置
均值/中位数/众数
截尾均值:去掉高低极致
中位数:对于倾斜非对称的数据,数据中心的更好度量
中位数近似值:书P47
中列数:数据集的最大和最小值的平均值
2.度量数据散布:极差/四分位数/方差/标准差/四分位数极差
极差:max和min的差
四分位数:把数据平均分配成四部分(二分位数对应于中位数)
四分位数极差(IQR)= Q3-Q1
识别离群点的规则一般是:Q3之上1.5IQR处或Q1之下1.5IQR
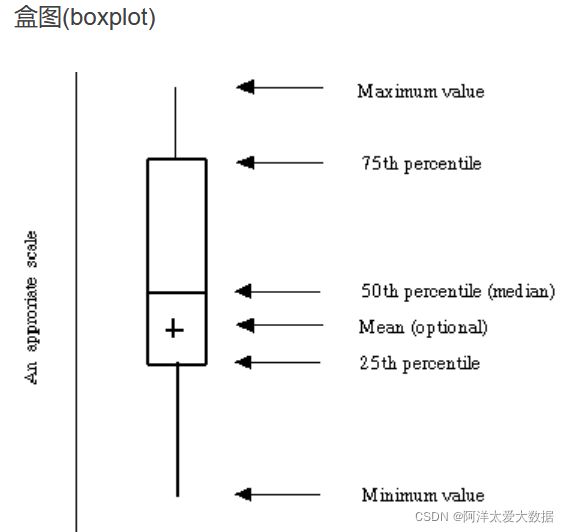
箱线图:体现了五数概括:分布的五数概括由中位数,四分位数Q1,Q3,最大最小观测值组成
胡须最大就是1.5IQR,也就是当最大值和最小值,都没有超过四分位数1.5IQR,则胡须就以最大最小值为端点,但若是存在有离群点,胡须则最大到1.5IQR处,离群点被个别绘出。
3.数据的基本统计描述的图形显示:分位数图/分位数-分位数图/直方图/散点图
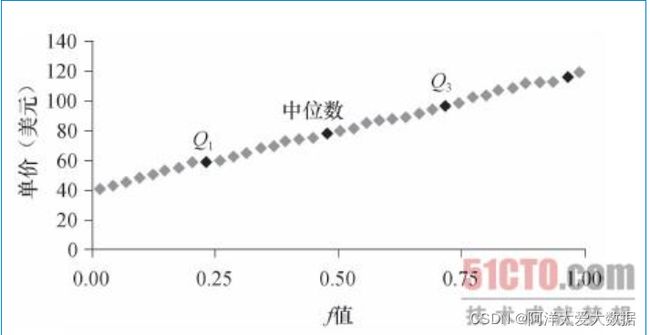
分位数图:
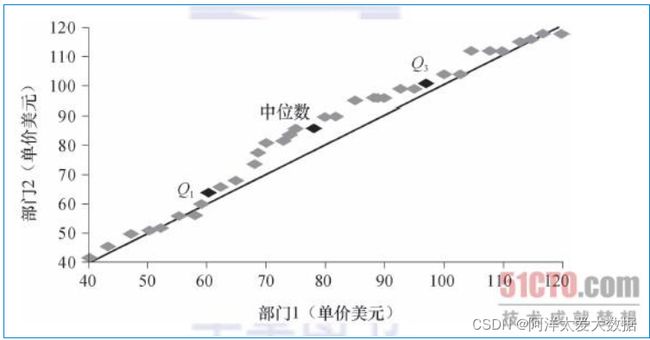
分位数-分位数图:Q-Q图
两个数据集,数据量相同,分别做(X,Y)画在图上,直线是辅助线
直方图:
散点图:确定两个变量看上去是否存在联系,模式或者趋势。观察双变量数据的有用办法
数据可视化:通过图形表示清晰有效的表达数据
基于像素的可视化技术:
几何投影可视化技术:
基于图符的可视化技术:
层次可视化技术
数据的相似性和相异性:
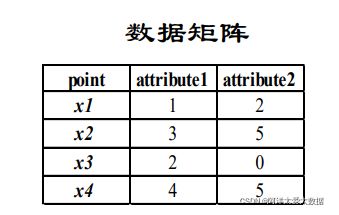
数据矩阵:
n*p 矩阵(n个对象,每个对象有p个属性)
相异度矩阵:
存储n个对象两两之间的相似性,表现形式是一个n×n维的矩阵。d(i,j)是对象i和j之间相异性的量化表示,通常为非负值,两个对象越相似或“接近”,其值越接近0,越不同,其值越大.
且d(i,j)= d(j,i),d(i,i)=0
例如:
主对角线元素为0,因为对象与对象本身被认为是没有差异的
d(i,j) = d(j,i),因此相异性矩阵是对称矩阵
相似度和距离:
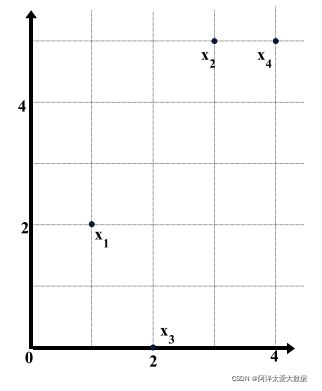
现在有4个数据点:x1、x2、x3、x4
它们的数据矩阵:
相异性矩阵(欧几里得距离)
度量数据的相似性和相异性:
数据矩阵由两种实体或“事物”组成,即行(代表对象)和列(代表属性)。因而,数据矩阵经常经常被称为二模矩阵。相异性矩阵只包含一类,因而被称为单模矩阵。
标称属性的邻近性度量:
两个对象i和j之间的相异性可以根据不匹配率来计算:
d( i , j ) = (p-m) / p
m : p个变量中匹配的个数(表示对象i与对象j之间有相同属性值的个数)注意是属性的个数
p : 全部变量的个数(标称属性的个数,而非某一个属性的值的个数)也是属性的个数,这里是总数
其中,m是匹配的数目(即i和j取值相同状态的属性数),而p是刻画对象的属性总数。我们可以通过赋予m较大的权重,或者赋给有较多状态的属性的匹配更大的权重来增加m的影响。
二元属性的邻近性度量
一种方法涉及由给定的二元数据计算相异性矩阵。如果所有的二元都被看做具有相同的权重,则我们得到一个两行两列的列联表——表2.3,其中q是对象i和j都取1的属性数,r是在对象i中取1、在对象j表2.3 二元属性的列联表对象i对象j中取0的属性数,s是在对象i中取0、在对象j中取1的属性数,而t是对象i和j都取0的属性数。属性的总数是p,其中p=q+r+s+t。
回忆一下,对于对称的二元属性,每个状态都同样重要。基于对称二元属性的相异性称做对称的二元相异性。如果对象i和j都用对称的二元属性刻画,则i和j的相异性为
对于非对称的二元属性,两个状态不是同等重要的;如病理化验的阳性(1)和阴性(0)结果。给定两个非对称的二元属性,两个都取值1的情况(正匹配)被认为比两个都取值0的情况(负匹配)更有意义。因此,这样的二元属性经常被认为是“一元的”(只有一种状态)。基于这种属性的相异性被称为非对称的二元相异性,其中负匹配数t被认为是不重要的,因此在计算时被忽略,如下所示:
互补地,我们可以基于相似性而不是基于相异性来度量两个二元属性的差别。例如,对象i和j之间的非对称的二元相似性可以用下式计算:
(2.15)式的系数sim(i,j)被称做Jaccard系数,它在文献中被广泛使用。
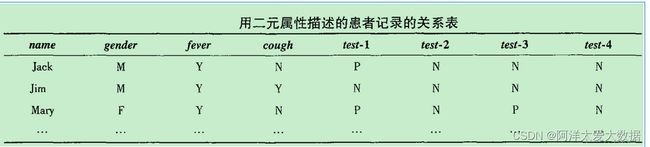
例子:
name是对象标识符,gender是对称属性,其余的属性都是非对称二元的。
对于非对称属性,值Y(yes)和P(positive)被设置为1,值N(no或negative)被设置为0。
Jack、Mary和Jim两两之间的距离如下:
因为具有最高的相异性,所以Jim和Mary不大可能患类似的疾病。而Jack和Mary最可能患类似的疾病。
式子是怎么得来的:
根据前面提到的二元属性的列联表:
因为name是对象标识符,gender是对称属性,其余的属性都是非对称二元的。所以只考虑gender、fever、cough、test1、test2、test3、test4这几个非对称属性。
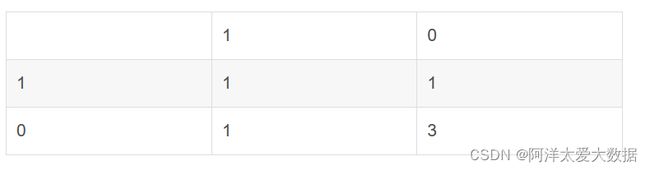
先以Jack和Jim为列子,列出这两个对象的二元属性列联表:
q是Jack和Jim非对称属性取值相同的属性个数,r、s、t依次类推
所以根据公式:
主要的关键就在于看两个对象众多属性值都取1,或者都取0,或者一个1一个0,这些都是在属性个数层面考虑的
数值的相异性:闵可夫斯基
计算数值属性刻画的对象的相异性的距离度量:欧几里得距离,曼哈顿距离,闵可夫斯基距离,最流行的距离度量是欧几里得距离(即,直线或“乌鸦飞行”距离)。令i=(xi1,xi2,…,xip)和j=(xj1,xj2,…,xjp)是两个被p个数值属性描述的对象。对象i和j之间的欧几里得距离定义为:
另一个著名的度量方法是曼哈顿(或城市块)距离,之所以如此命名,是因为它是城市两点之间的街区距离(如,向南2个街区,横过3个街区,共计5个街区)。其定义如下:
欧几里得距离和曼哈顿距离都满足如下数学性质:
非负性:d(i,j)≥0:距离是一个非负的数值。
同一性:d(i,i)=0:对象到自身的距离为0。
对称性:d(i,j) = d(j,i):距离是一个对称函数。
三角不等式:d(i,j)≤d(i,k)+d(k,j):从对象i到对象j的直接距离不会大于途经任何其他对象k的距离。
满足这些条件的测度称做度量(metric)。注意非负性被其他三个性质所蕴含。
闵可夫斯基距离:
当p=2时,闵可夫斯基距离即欧氏距离(Euclidean distance) :
当p=1时,闵可夫斯基距离即曼哈顿距离(Manhattan distance),亦称“街区距离”(city block distance):
当p→∞时,闵可夫斯基距离即切比雪夫距离(Chebyshev distance):
数据预处理
数据清理/数据集成/数据规约/数据变换
数据质量 :准确性,完整性,一致性,时效性,可信性,可解释性
预处理:
数据清理:列如填写缺失值,光滑噪声,识别删除离群点,解决不一致性。
第一步:偏差检测(表单设计糟糕,人为出错,数据退化,数据集成也可能导致不一致q)
元数据:“关于数据的数据”
数据清洗工具,数据审计工具,数据迁移工具,ETL工具
缺失值:
填充方法:
- 忽略元组
- 人工填写缺失值
- 使用一个全局常量填充缺失值
- 使用属性的中心度量
- 使用与给定元组属同一类的所有样本的属性均值或中位数
- 使用最可能的值填充缺失值
缺失数据背景:条件缺失,完全随机缺失
噪声和异常:异常比噪声离谱
数据光滑方法:(也可用于数据离散化和数据规约)
分箱:通过考察数据的近邻来光滑有序的数据值
回归:用函数拟合来光滑数据
离群点分析:可以通过聚类来检测离群点
数据集成:集成多个数据库,数据立方体,或者文件(代表同一属性和概念可能在不同的数据库有不同的命名,这导致了不一致性和冗余)
1.实体识别2.冗余相关分析3.元组重复4.数值冲突的检测与处理
- 实体识别问题:怎么确定两个数据集不同名字的两个属性是同一个?
每个属性的元数据包含名字,取值范围,空值,数据类型
- 冗余和相关分析:
- 标称数据的卡方相关检验:
卡方统计检验假设A和B是独立的。
假设调查了1500个人,记录性别,是否小说,那么有两个属性:性别、是否喜欢小说:
单元(男,小说)的期望频率是:
e11=count(男)*count(小说)/n=300*450/1500=90
根据公式:
Oij表示观察到的(Ai,Bj)联合事件的概率(实际出现的次数),eij表示(Ai,Bj)期望频率,计算公式:
期望频率计算:n是元组的总个数
假定属性AB相互独立的,属性A有r种取值(如头发颜色红黄蓝)B有c中不同取值,基于显著性水平,自由度是(r-1)*(c-1)。
根据卡方值公式:
自由度是(2-1)(2-1)=1
- 数值数据的相关系数
又称皮尔逊积矩系数,估计两个属性的相关度rA,B
其中,n是元组个数,ai和bi分别是元组i在A和B上的值,![]() 和
和![]() 分别是AB的均值
分别是AB的均值![]() 分别是AB的标准差。
分别是AB的标准差。
-1≤rA,B≥1![]() ,大于0正相关,小于0 负相关,值越大,相关性越强
,大于0正相关,小于0 负相关,值越大,相关性越强
协方差:
- 元组重复
- 数值冲突检测与处理
数据规约:降低数据集的规模,但是又不损害数据挖掘的结果。得到数据集的简化表示,小得多但是能产生同样的结果。
维归约,数量规约,数据压缩
小波变换,
主成分分析
属性子集选择
回归和对数线性模型:参数化数据规约
直方图
聚类
抽样:无放回简单随机抽样,有放回简单随机抽样,簇抽样,分层抽样
数据立方体聚集
维归约:使用数据编码方案,。列子包括数据压缩技术(小波变换和主成分分析),及属性子集选择(去掉不相关的属性)和属性选择(导出更小更有用的属性集)
数值规约:使用参数模型(回归和对数线性模型),非参数模型(直方图,聚类,抽样,数据聚集)
数据变换:规范化,数据离散化,概念分层
数据变换策略:
- 光滑
- 属性构造
- 聚集
- 离散化
- 由标称数据产生概念分层:属性
通过规范化变化数据:
挖掘频繁模式,关联和相关性;基本概念和方法
- 项集:项的集合,k个项称为k项集,列如:集合{“啤酒”, “咖啡”, “鸡蛋”},是一个项集,项集的出现频度:包含项集的事务数(用集合里面的属于概念来表征)
- 事务:每一个事务是一个非空项集(购物日志,每次购物行为是一个事务),并拥有一个标识TID(表1)
- 数据集:事务的集合
- 支持度计数/绝对支持度(support count):数据集中包含项集X的事物数
- 相对支持度(support):项集X的绝对支持度与数据集事物总数的比值
- 频繁项集(frequent itemset):项集X的支持度超过最小门限值min_sup时,称X为频繁项集
频繁项集的压缩表示:
- 闭频繁项集:当项集X是频繁项集,且数据集D中不存在X的真超集Y,使得X和Y的支持度相等,则X是闭频繁项集。闭频繁项集的表示是无损压缩,不会丢失支持度的信息。通过闭频繁项集可以反推出所有的频繁项集以及相应的支持度(理解:向项集任意增加一个项,项集出现的频度就会发生改变)
闭频繁项集包含了频繁项集的完整信息
- 极大频繁项集:当项集X是频繁项集,且数据集D中不存在X的真超集Y,使得Y是频繁项集,则X是极大频繁项集。极大频繁项集的表示是有损压缩,失去了频繁项集的支持度信息,我们可以根据极大频繁项集判断任意项集是否是频繁的,但无法得到相应的支持度(理解:加入任何一个项,项集就不是频繁的了)
频繁项集的挖掘:
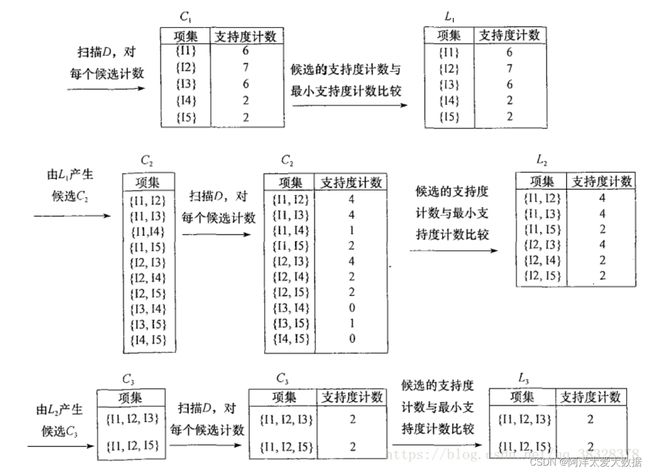
Apriori算法:基于支持度的剪枝方法
Apriori原理:如果某个项集是频繁的,那么它的所有子集也是频繁的。该定理的逆反定理为:如果某一个项集是非频繁的,那么它的所有超集(包含该集合的集合)也是非频繁的。Apriori原理的出现,可以在得知某些项集是非频繁之后,不需要计算该集合的超集,有效地避免项集数目的指数增长,从而在合理时间内计算出频繁项集。
算法思想:
①找出所有的频集,这些项集出现的频繁性至少和预定义的最小支持度一样。
②由频集产生强关联规则,这些规则必须满足最小支持度和最小可信度。
③使用第1步找到的频集产生期望的规则,产生只包含集合的项的所有规则,其中每一条规则的右部只有一项,这里采用的是中规则的定义。
④一旦这些规则被生成,那么只有那些大于用户给定的最小可信度的规则才被留下来。为了生成所有频集,使用了递推的方法。
Ariori算法有两个主要步骤:
1、连接:(将项集进行两两连接形成新的候选集)
利用已经找到的个项的频繁项集,通过两两连接得出候选集,注意进行连接的,,必须有个属性值相同,然后另外两个不同的分别分布在,中,这样的求出的为的候选集。
2、剪枝:(去掉非频繁项集)
候选集中的并不都是频繁项集,必须剪枝去掉,越早越好以防止所处理的数据无效项越来越多。只有当子集都是频繁集的候选集才是频繁集,这是剪枝的依据
- 关联规则:
是形如X→Y(s,c)的表达式,其中X和Y均为项集,且X∩Y=∅
1.支持度一个事物包含X∪Y的概率
2.置信度,条件概率,买了X的人又买了Y的比例有多少,表示关联性的强弱,或者说是规则的可靠性:
关联规则的挖掘:
第一步:找出所有频繁项集
第二步:由频繁项集产生强关联规则
FP-Growth算法:
在关联分析中,频繁项集的挖掘最常用到的就是Apriori算法。Apriori算法是一种先产生候选项集再检验是否频繁的“产生-测试”的方法。这种方法有种弊端:当数据集很大的时候,需要不断扫描数据集造成运行效率很低。
而FP-Growth算法就很好地解决了这个问题。它的思路是把数据集中的事务映射到一棵FP-Tree上面,再根据这棵树找出频繁项集。FP-Tree的构建过程只需要扫描两次数据集
算法步骤
FP-growth算法发现频繁项集的基本过程如下:
①构建FP树;
②从FP树中挖掘频繁项集;
输入:数据集、最小值尺度
输出:FP树、头指针表
1、遍历数据集,统计各元素项出现次数,创建头指针表
2、移除头指针表中不满足最小值尺度的元素项
3、第二次遍历数据集,创建FP树。对每个数据集中的项集:
3.1 初始化空FP树
3.2 对每个项集进行过滤和重排序
3.3 使用这个项集更新FP树,从FP树的根节点开始:
3.3.1 如果当前项集的第一个元素项存在于FP树当前节点的子节点中,则更新这个子节点的计数值
3.3.2 否则,创建新的子节点,更新头指针表
3.3.3 对当前项集的其余元素项和当前元素项的对应子节点递归3.3的过程
详解:
FP-growth算法将数据存储在一个称为FP树的紧凑数据结构中,它与计算机科学中的其他树的结构类似,但是它通过链接来链接相似元素,被连起来的元素可以看做一个链表,如下图:
FP树会存储项集出现的频率,每个项集都会以路径的形式存储在树中,存在相似元素的集合会共享树的一部分。只有当集合之间完全不同时树才会分叉,树节点上给出集合中单个元素及其在序列中出现的次数,路径会给出该序列的出现次数。
相似项之间的链接即节点链接,用于快速发现相似项的位置,下面的例子:
第一列是事务的ID,第二列是事务中的元素项,在图1中z出现了5次,而{r,z}项支出项了一次,所以z一定自己本身或者和其他的符号一起出现了4次,而由图1同样可知:集合{t,s,y,x,z}出现了2次,集合{t,r,y,x,z}出现了1次,所以z一定本身出现了1次。看了图2可能会有疑问,为什么在图1中没有p,q,w,v等元素呢?这是因为通常会给所有的元素设置一个阈度值(Apriori里的支持度),低于这个阈值的元素不加以研究。暂时不理解没关系,看了下面的内容可能会对这一段的内容有比较好的理解。
建FP树是算法的第一步,在FP树的基础之上再对频繁项集进行挖掘。为了构建FP树,要对数据集扫描两次,第一次对所有元素项出现次数进行计数,记住如果一个元素不是频繁的,那么包含这个元素的超集也不是频繁的,所以不需要考虑这些超集,第二遍的扫描只考虑那些频繁元素。
除了图1给出的FP树之外,还需要一个头指针表来指向给定类型的第一个实例。利用头指针表可以快速访问FP树中一个给定类型的所有元素,发现相似元素项,如下图所示:
头指针表的数据结构是字典,除了存放头指针元素之外,还可以存放FP中每类元素的个数。第一次遍历数据集得到每个元素项出现的频率,接下来去掉不满足最小值支持度的元素项,在接下来就可以创建FP树了,构建时,将每个项集添加到一个已经存在的路径中,如果该路径不存在,则创建一个新的路径。每个事务都是一个无序的集合,然而在FP树中相同项只会出现一次,{x,y,z}和{y,z,x}应该在同一个路径上,所以在将集合添加到树之前要对每个集合进行排序,排序是基于各个元素出现的频率来进行的,使用图3头指针表中单个元素的出现值,对图2中的数据进行过滤,重排后的新数据如下:
现在,就可以构建FP树了,从空集开始,向其中不断添加频繁项集。过滤,排序后的事务依次添加到树中,如果树中已有现有元素,则增加该元素的值;如果元素不存在,则添加新分枝。图4中事务表前两条事务添加的过程如下图所示:
从FP树中抽取频繁项集的三个基本步骤:
1)从FP树中获得条件模式基;
2)利用条件模式基,构建一个条件FP树;
3)迭代重复步骤(1)(2)直到树只包含一个元素项为止
分类
回归分析是数值预测的最常用的方法
数据分类两阶段:学习阶段和分类阶段
提供了训练元组的类:监督学习
无监督学习(聚类)
分类过程的第一阶段:也可以看做学习一个映射或函数y = f(X),
分类的第二阶段:使用模型进行分类
决策树:自顶向下递归树归纳算法,
朴素贝叶斯分类:基于后验概率
基于规则的分类器:使用IF-THEN规则进行分类
IF 条件 then 结论 (IF部分为前提,then部分是结论)
可以用覆盖率和准确率来评估:
规则R可以用它的覆盖率和准确率来评估。给定类标记的数据集D中的一个元组X,设ncovers为覆盖的元组数,ncorrect为R正确分类的元组数,可以将R的覆盖率和准确率定义为:
混淆矩阵:评估分类器的质量
基于规则的分类:
覆盖率
准确率
同时满足多个规则:
规模序
规则序(基于类的和基于规则的)
不存在X满足规则的情况
建立一个省缺或默认规则
由决策树提取规则
使用顺序覆盖算法的规则归纳