机器学习之K-means聚类分析

K-means算法的目标

K-means是一种出发点最直观的聚类算法，在使用过程中只需要人为指定需要被划分组的数量。然后它将样本向量中距离最近的一些点划分到一组中。K-means算法的目标就是在假定要聚类的每个小组中有一个中心点，K-means算法的目的就是找到这些中心点的坐标，使得所有样本向量到其分组中心点的距离平方和最小。用数学公式表示为：
$$C=\sum _{i=1...N}distant(centerOf(x_i)-y_i{)}^2$$
其中$y_i$是样本特征向量，centerOf($x_i$)是样本所在组的中心点向量，distant用于计算两个向量之间的距离，每个距离值累加得到C值。

K-means算法的步骤(实现过程)

K-means算法在使用过程中是需要人为指定需要划分组的数量，所以我们假设数据集需要被划分为M个组，首先，我们可以用固定值或者随机的方式选取任意M个点作为每组的中心点，然后迭代执行下面两步：1：为每个中心点找到各自的样本数据，一个样本数据距离哪个中心点近则被划分给哪个中心点；2：在每个组内用该组成员重新计算出中心点新的中心点坐标是组内每个成员在各维度上的算术平均值，新的中心点确定好后的C值一定低于或等于原来的C值。
一直迭代循环这两步，直到C值低于某个要求或者每组中被推荐的中心点不在发生变化（C值不在变化）,算法结束退出。下面的gif动图就是K-means算法的运行过程。

图片来源：https://pic2.zhimg.com/v2-169818722555497ae9d461a7352fabd1_b.webp

k值的选择(就是需要划分组的数量)

在使用K-means算法前，我们需要给出划分组的数量（K值），但一些数据集并不明确可以分成几组，所以，这时，要划分组的数量就成了问题。而且，在不同的场景中K值的选择没有固定的标准。在K-means聚类算法结果有一个衡量标准是inertia_值，它的值越小越好，因为该值越小说明每组的成员之间的距离越近。但是，随着K值的增加，inertia_值会越来越小，直到K值等于样本数量时，inertia_值为0。在任何数据集上，K值与inertia_是相反关系的，可以将K值的增大看成一种对inerta_的减小的贡献。但显然K值不能无线增大，因为这样就失去了聚类的意义。那么我们应该怎么找到适合的K值呢？其实有一个比较直观的方法是肘部法—给定一定范围的K值，循环得出inertia_，然后会出可视化图，选择对inertia_贡献效果已经不显著的K值点(就是线段转向平缓的拐点)。下面我们使用代码来实践下。

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import numpy as np

# 创建训练数据
c1x = np.random.uniform(0.5, 1.5, (1, 20))
c1y = np.random.uniform(0.5, 1.5, (1, 20))
c2x = np.random.uniform(3.5, 4.5, (1, 20))
c2y = np.random.uniform(3.5, 4.5, (1, 20))
x = np.hstack((c1x, c2x))
y = np.hstack((c2y, c2y))
X = np.vstack((x, y)).T

# 导入模型
kemans = KMeans(n_clusters=2)
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']  # 散点图标签可以显示中文
# 采用肘部法选择K值
K = range(1, 10)
meanDispersions = []
for k in K:
    kemans = KMeans(n_clusters=k)
    kemans.fit(X)
    # 计算平均离差
    m_Disp = sum(np.min(cdist(X, kemans.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0]
    meanDispersions.append(m_Disp)
plt.plot(K, meanDispersions, 'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
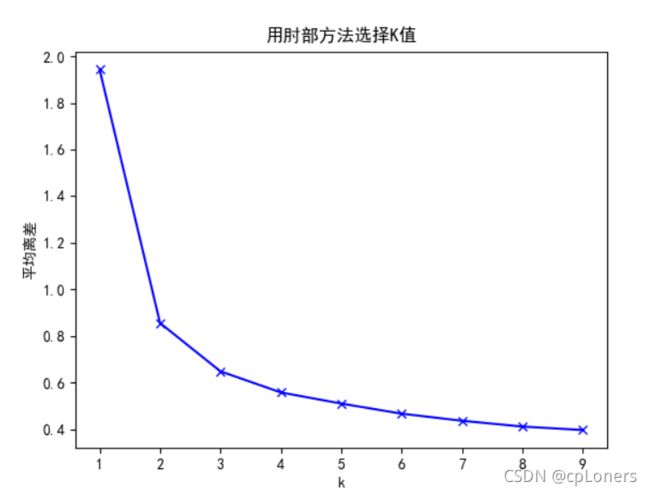
plt.title('用肘部方法选择K值')
plt.show()

显然，2是一个比较稳妥的K值选择，当数据的特征维度较高无法直接视觉识别时，采用查找K值曲线拐点的方法还是可以找出合适的K值。

K-means实战

实战我们使用sklearn.datasets中的load_iris数据集

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
import numpy as np
from scipy.spatial.distance import cdist
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split


# 导入数据
iris = load_iris()
datas = iris.data
target = iris.target
train_data, test_data, train_target, test_target = train_test_split(datas, target, test_size=0.2)
# 选择K值
kemans = KMeans(n_clusters=2)
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']  # 散点图标签可以显示中文
# 采用肘部法选择K值
K = range(1, 10)
meanDispersions = []
for k in K:
    kemans = KMeans(n_clusters=k)
    kemans.fit(datas)
    # 计算平均离差
    m_Disp = sum(np.min(cdist(datas, kemans.cluster_centers_, 'euclidean'), axis=1)) / datas.shape[0]
    meanDispersions.append(m_Disp)
plt.plot(K, meanDispersions, 'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()
# 训练
clf = KMeans(n_clusters=3, init='random')
clf.fit(train_data, train_target)
print("测试集评分：", clf.score(train_data, train_target))

这时的K值为3是一个比较稳妥的选择。

在有监督学习模型中(之前学的回归等都是有监督学习)，score()函数是通过比较预测目标与真实目标值来评估模型数据的拟合度。但在无监督学习的模型中，score()函数只能用于衡量模型对测试数据的分组信任。比如在上面的K-means中，测试数据里中心点越近则返回score()分值越高，反之则低。所以当score()返回-0.0时，则说明测试数据都落在中心点上。最后，我们用一个表格来总结解析下sklearn中的K-means常用的初始化参数

参数	解析
n_clusters（上面所说的K值）	生成的聚类(分组)数。
max_iter	执行一次k-means算法所进行的最大迭代数
n_init	用不同的聚类中心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果
init	有三个可选值：’k-means++’， ‘random’，或者自定义一个ndarray向量；‘k-means++’是 用一种特殊的方法选定初始聚类中发，可加速迭代过程的收敛。‘random’ 随机从训练数据中选取初始质心。
precompute_distances	三个可选值，‘auto’，True 或者 False；‘auto’：如果 样本数乘以聚类数大于 12million 的话则不预计算距离。True：总是预先计算距离。False：永远不预先计算距离
tol	float类型，默认值= 1e-4　与inertia结合来确定收敛条件