数据结构与算法笔记

看了《算法精粹——经典计算机科学问题的Python实现》这本书，记录了一些笔记，整理了此篇文章，持续更新…

0.序言

0.1数据结构

参考文章：最全的数据结构归纳总结

0.2斐波那契数列（递归）

斐波那契序列（Fibonacci sequence）是一系列数字，后面的数字是前两个数字之和。$$fib(n)=fib(n-1)+fib(n-2)$$

一般用递归编写fib函数，递归包括基线条件和递归条件。

"""
    利用字典对象作为结果缓存
"""
from typing import Dict
memo: Dict[int, int] = {0: 0, 1: 1}  # base cases

def fib3(n: int) -> int:
    if n not in memo:
        memo[n] = fib3(n - 1) + fib3(n - 2)     # memoization
    return memo[n]

0.3距离

• 欧氏距离（Euclidean distance）：对角线距离，$d=\sqrt{\Delta x^2+\Delta y^2}$
• 曼哈顿距离（Manhattan distance）：绝对值距离，$d=|x|+|y|$

1.排序

1.1冒泡排序

def bubble_sort(alist):
    for j in range(len(alist) - 1, 0, -1):
        # j表示每次遍历需要比较的次数，是逐渐减小的
        for i in range(j):
            if alist[i] > alist[i + 1]:
                alist[i], alist[i + 1] = alist[i + 1], alist[i]

li = [54, 26, 93, 17, 77, 31]
bubble_sort(li)
print(li)

1.2选择排序

def selection_sort(alist):
    n = len(alist)
    # 需要进行n-1次选择操作
    for i in range(n - 1):
        min_index = i
        for j in range(i + 1, n):
            if alist[j] < alist[min_index]:
                min_index = j
        # 如果选择出的数据不在正确位置，进行交换
        if min_index != i:
            alist[i], alist[min_index] = alist[min_index], alist[i]

li = [54, 26, 93, 17, 77, 31]
selection_sort(li)
print(li)

1.3插入排序

def insert_sort(alist):
    for i in range(1, len(alist)):
        # 从第i个元素开始向前比较，若小于前一个元素则交换位置
        for j in range(i, 0, -1):
            if alist[j] < alist[j - 1]:
                alist[j], alist[j - 1] = alist[j - 1], alist[j]

li = [54,26,93,17,77,31]
insert_sort(li)
print(li)

1.4快速排序

简单版本的：

def quicksort(array):
    # 基线条件
    if len(array) < 2:
        return array
    # 递归条件
    else:
        pivot = array[0]
        less = [i for i in array[1:] if i <= pivot]
        greater = [i for i in array[1:] if i > pivot]
        return quicksort(less) + [pivot] + quicksort(greater)
        
print (quicksort([10, 5, 2, 3]))

1.5希尔排序

def shell_sort(alist):
    n = len(alist)
    gap = n // 2     # 初始步长
    while gap > 0:
        # 按照步长进行插入排序
        for i in range(gap, n):
            j = i
            # 插入排序
            while j >= gap and alist[j - gap] > alist[j]:
                alist[j - gap], alist[j] = alist[j], alist[j - gap]
                j -= gap
        # 得到新的步长
        gap = gap // 2

li = [54, 26, 93, 17, 77, 31]
shell_sort(li)
print(li)

1.6归并排序

def merge_sort(alist):
    if len(alist) <= 1:
        return alist
    # 二分分解
    num = len(alist) // 2
    left = merge_sort(alist[: num])
    right = merge_sort(alist[num :])
    # 合并
    return merge(left, right)

def merge(left, right):
    # 合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组
    l, r = 0, 0     # left和right的下下标指针
    result = []
    while l < len(left) and r < len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]
    result += right[r:]
    return result

li = [54,26,93,17,77,31]
print(merge_sort(li))

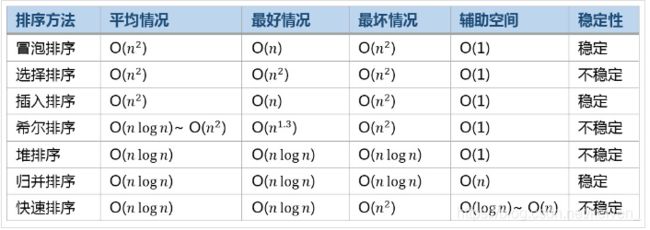
1.7总结

这里有一个贼nb的总结：十大经典排序算法（动图演示）

2.搜索算法

2.1线性搜索（Linear search）

按照原始数据结构的顺序遍历搜索空间（search space）中的每个元素。时间复杂度为$O(n)$。

2.2二分搜索（Binary search）

查看一定范围内有序元素的中间位置的元素，将其与所查找的元素进行比较，根据比较结果将搜索范围缩小一半，重复上述过程。

2.3深度优先搜索（Depth-first search）

DFS深度优先搜索：搜索尽可能深深入，碰到障碍就回溯到最后一次的决策位置。栈作为基本数据结构。

2.4广度优先搜索（Breadth-first search）

BFS广度优先搜索：寻找最短路径，离起点位置最近的元素最先被搜索。队列作为基本数据结构。

2.5A*搜索

A*搜索结合运用代价函数与启发函数。优先队列作为基本数据结构。

2.6总结

参考文章：搜索算法总结

3.约束满足问题（Constraint-satisfaction problem）

CSP约束满足问题由一组变量构成，变量可能的取值范围是值域（domain）,要求解决约束满足问题需要满足变量之间的约束。CSP是变量、值域和约束的汇聚点。

参考文章：人工智能 一种现代方法 第6章 约束满足问题

4.图问题

4.1贪婪算法

每一步都寻找最优解，最终解不一定是最优解。

参考文章：【算法】贪婪算法（贪心算法）

4.2Jarnik算法

一种贪婪算法，不适用于有向图和非连通图

参考文章：最小生成树之Prim（普里姆）算法

4.3Dijkstra算法

通过更新的方式寻找起点到终点的最短路径。

参考文章：最短路径问题—Dijkstra算法详解

5.遗传算法（Genetic algorithm）

遗传算法包含了名为染色体（chromosome）的个体组成的种群。所有染色体都要竞争解决一些问题，每条染色体都由定义其特性的基因组成。染色体解决问题的能力由适应度函数（fitness function）定义。遗传算法要经历很多代（generation）。每一代中适应力较强的染色体更有可能被选中进行繁殖。每一代中还有可能发生两条染色体的基因合并，即交换（crossover）。染色体的基因可能会随机发生变异（mutate）。所以染色体必须实现以下功能：

• 确定自己的适应度
• 创建一个携带了随机选中基因的实例（用于填充第一代个体的数据）
• 实现交换，让自己与另一个同类结合并创建后代
• 变异，让自己体内的数据发生相当随机的小变化

常见的两种遗传算法的选择方法：

• 轮盘式选择法（Roulette-wheel selection）：有时被称为适应度比例选择法（Fitness proportionate selection），让每一条染色体都有机会被选中，与其适应度成正比。
• 锦标赛选择法（Tournament selection）：一定数量的随机染色体会相互挑战，适应度最佳的那个染色体将会被选中。

参考文章：遗传算法详解（GA）（个人觉得很形象，很适合初学者）

6.K均值聚类（K-means clustering）

K均值聚类算法：根据每个点与聚类簇中心的相对距离，将聚类点分组到某个聚类簇中。是一种非监督学习方法。

kmeans++算法：不是完全随机选择形心，而是基于到各点距离的概率分布选择形心。

参考文章：Kmeans聚类算法详解

7.对抗搜索（adversarial search）

7.1极小化极大算法

极小化极大算法通常采用递归实现，两个玩家要么是极大化玩家，要么是极小化玩家。极大化玩家目标是找到能获得最大收益的走法，但是必须考虑极小化玩家的走法，即需要求得对手的回手：让极大化玩家的收益最小化的走法。这个过程一直进行（求最大值、求最小值），直到达到递归函数的基线条件。对于搜索空间太深而无法抵达终局的游戏，极小化极大函数minimax()会在达到一定深度后停止。

7.2α-β剪枝算法（alpha-beta pruning）优化极小化极大算法

在搜索时将不会生成更优结果的棋局排除，由此来增加搜索的深度。跟踪记录递归调用minimax()间的两个值$\alpha$和$\beta$，$\alpha$表示搜索树当前找到的最优极大化走法的评分，$\beta$表示当前找到的对手的最优极小化走法的评分，如果$\beta \le \alpha$，则不值得对该搜索分支进一步搜索。这种启发式算法能显著缩小搜索空间。

参考文章：极小化极大算法