数据结构与算法python北大版笔记 - 动态规划
优化问题和贪心策略
1.找零兑换问题:兑换最少个数的硬币问题
贪心策略:
从最大面值的硬币开始,用尽量多的数量有余额的,再到下一个最大面值的硬币,还用尽量多的数量,一直到penny($1)为止
1)递归解法:
首先确定基本结束条件,兑换硬币问题最简单直接的情况就是,需要兑换找零,其面值正好等于某种硬币。
其次是减少问题的规模,对每种硬币尝试一次(如美元硬币体系):
- 找零减去1分后,求兑换硬币最少数量
- 找零减去5分后,求兑换硬币最少数量
- 找零减去10分后,求兑换硬币最少数量
- 找零减去25分后,求兑换硬币最少数量
上述4项中选择最小的一个。
def recMC(coinValueList,change):
minCoins = change
if change in coinValueList:
return 1
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMC(coinValueList,change-i)
if numCoins < minCoins:
minCoins = numCoins
return minCoins
print(recMC([1,5,10,25],11))
以上递归解法存在大量重复计算。
2)递归解法改进
用一个表将计算过的中间结果保存起来,在计算前查看是否已经计算过。
这个算法的中间结果就是部分找零的最优解,在递归调用过程中已经达到的最优解记录下来。
- 在递归调用之前,先查找表中是否已有部分找零的最优解
- 如果有,直接返回最后节而不进行递归调用
- 如果没有,才进行递归调用
def recMC(coinValueList,change,knowResults):
minCoins = change
if change in coinValueList: # 递归基本结束条件
knowResults[change] = 1 # 记录最优解
return 1
elif knowResults[change] > 0:
return knowResults[change] # 查表成功,直接用最优解
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMC(coinValueList,change-i,knowResults)
if numCoins < minCoins:
minCoins = numCoins
#找到最优解,记录到表中
knowResults[change] = minCoins
return minCoins
print(recMC([1,5,10,25],63,[0]*64))
3)动态规划解法
找零兑换的动态规划算法从最简单的“1分钱找零”的最优解开始,逐步递加上去,直到我们需要的找零钱数。在找零递加的过程中,设法保持每一分钱的递加都是最优解,一直加到求解找零钱数,自然得到最优解。
问题的最优解包含了更小规模子问题的最优解,这是一个最优化问题能够用动态规划策略解决的必要条件。
def dpMakeChange(coinValueList,change,minCoins):
#从1分开始到change逐个计算最少硬币数
for cents in range(1, change+1):
# 1.初始化一个最大值
coinCount = cents
# 2.减去每个硬币,向后查最少硬币数,同时记录总的最少数
for j in [c for c in coinValueList if c <= cents]:
if minCoins[cents - j] + 1 < coinCount:
coinCount = minCoins[cents - j] + 1
# 3.得到当前最少硬币数,记录到表中
minCoins[cents] = coinCount
# 返回最后一个结果
return minCoins[change]
print(dpMakeChange([1,5,10,21,25],63,[0]*64))
动态规划的主要思想是:
- 从最简单情况开始到达所需找零的循环
- 其每一步都依靠以前的最优解来得到本步骤的最优解,直到得到答案
3)动态规划解法扩展:记录最少硬币数量的组合
def dpMakeChange(coinValueList, change, minCoins, coinsUsed):
#从1分开始到change逐个计算最少硬币数
for cents in range(1, change+1):
# 1.初始化一个最大值
coinCount = cents
newCoin = 1 # 初始化一下新加的硬币
# 2.减去每个硬币,向后查最少硬币数,同时记录总的最少数
for j in [c for c in coinValueList if c <= cents]:
if minCoins[cents - j] + 1 < coinCount:
coinCount = minCoins[cents - j] + 1
newCoin = j # 最小对应数量,所减的硬币
# 3.得到当前最少硬币数,记录到表中
minCoins[cents] = coinCount
coinsUsed[cents] = newCoin # 记录本步骤加的1个硬币
# 返回最后一个结果
return minCoins[change]
def printCoins(coinsUsed, change):
coin = change
while coin > 0:
thisCoin = coinsUsed[coin]
print(thisCoin)
coin = coin - thisCoin
amnt = 63
clist = [1, 5, 10, 21, 25]
coinsUsed = [0] * (amnt+1)
coinCount = [0] * (amnt+1)
print("Making change for", amnt, "requires")
print(dpMakeChange(clist, amnt, coinCount, coinsUsed), "coins")
print("They are:")
printCoins(coinsUsed, amnt)
print("The used list is as follows:")
print(coinsUsed)
2.博物馆大盗问题
大盗潜入博物馆,面前有5件宝物,分别有重量和价值,大盗的背包仅能负重20公斤,请问如何选择宝物,总价值最高?
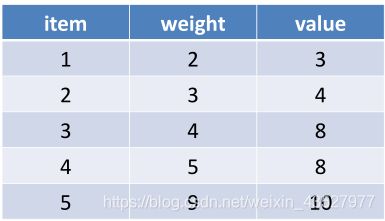
动态规划:
我们把 m(i i, , W) 记为:前i(1<=i<=5) 个宝物中,组合不超过W(1<=W<=20) 重量,得到的最大价值m(i, W) 应该是m(i-1, W) 和m(i-1, W-W i )+v i两者最大值我们从m(1, 1) 开始计算到m(5, 20)
# 宝物的重量和价值
tr = [None, {'w': 2, 'v': 3}, {'w': 2, 'v': 3},
{'w': 2, 'v': 3}, {'w': 2, 'v': 3},
{'w': 2, 'v': 3}]
# 大盗最大承重
max_w = 20
# 初始化二维表格m[m(i,w)]
# 表示前i个宝物中,最大重量w的组合,所得到的最大价值
# 当i什么都不取,或w上限为0,价值均为0
# 二维表初始化
m = {(i, w): 0 for i in range(len(tr)) for w in range(max_w + 1)}
#逐个填写二维表格
for i in range(1, len(tr)):
for w in range(1, max_w + 1):
if tr[i]['w'] > w: #装不下第i个宝物
m[(i, w)] = m[(i-1, w)]
else:
# 不装第i个宝物,装第i个宝物,两种情况下最大价值
m[(i, w)] = max(m[(i, w)], m[(i-1, w-tr[i]['w'])] + tr[i]['v'])
#输出结果
print(m[(len(tr)-1, max_w)])
递归:
# 宝物的重量和价值
tr = {(2, 3), (3, 4), (4, 8), (5, 8), (9, 10)}
# 大盗最大承重
max_w = 20
# 初始化记忆化表格m:记录中间值
# key是(宝物组合,最大重量),value是最大价值
m = {}
def theif(tr, w):
if tr == set() or w == 0:
m[(tuple(tr), w)] = 0 # tuple是key的要求
return 0
elif (tuple(tr), w) in m:
return m[(tuple(tr), w)]
else:
vmax = 0
for t in tr:
if t[0] <= w:
# 逐个从集合中去掉某个宝物,递归调用
# 选出所有价值中的最大值
v = theif(tr - {t}, w - t[0]) + t[1]
vmax = max(vmax, v)
m[(tuple(tr), w)] = vmax
return vmax
# 输出结果
print(theif(tr, max_w))


