【零基础】学python数据结构与算法笔记14-动态规划

---

前言

学习python数据结构与算法，学习常用的算法，
b站学习链接

88.动态规划介绍

动态规划在基因测序、基因比对、hmm 有应用场景。

从斐波那契数列看动态规划

练习： 使用递归和非递归的方法来求解斐波那契数列。

这种非递归求斐波那契数，可以看成是一个动态规划思想，每次都会把重复子问题的答案存起来。

89.钢条切割问题

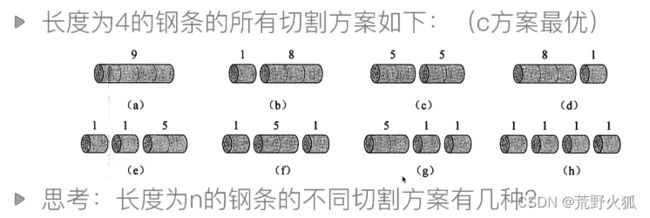
长度为n的一共有n-1口可以切，每一口可以选择切或者不切，所以有2^n-1种不同的方法。

r[i]那行是长度为i时，最多买的钱。可以这样考虑，在长度为2时，可以选择切成1和1 或者不切，不切最大利润是5，切了后最大利润是2，把最大利润存到r[2]下，当r[3]时，可以不切或者切成1和2（不考虑切成1、1、1，因为在r[2]中已经考虑过1和1 的利润没2大），选择最大的8存放在r[3]中，按照这样的思想，比方说看r[9],看不切或1和8或2和7或3和6或4和5，选择最大的放到r[9],
先看1和8，1+22
2和7，5+18
3和6，8+17
4和5，10+13
于是我们可以推出递推式，不切和切一刀之后最大值就是利润最大。此时从左边往右边切和从右边往左切是一样的，但我们还是考虑了切成5和4，切成6和3的情况。

我们可以将求解规模为n的原问题划分成规模更小的子问题：完成一次切割后，可以将产生的两端钢条看成两个独立的钢条切割问题，

这就叫最优子结构，把9的最大=3最大+6最大。

此时可以得出以上的递推式，不过还可以再进行简化，以上是不切和切一次的不同位置来构成的递推式。

这样还是切9， 左边一部分是不切的，所以价值是原来不切的价值
1和8，1+20
2和7，5+18
3和6，8+17
4和5，9+13
5和4，10+10
6和3，17+8
7和2，17+5
8和1，20+1
25还是最大，为什么可以这样做呢？因为现在最大是3和6 实则是3和6，但假设如果最大是23 那就是2和2和2和3，2没切，后面的7切成了三段，或者假设说是4和5，4没切，5切成2和3，那么就是说，这样左边没切，右边切，所有的情况还是都能列举，之前的方法有重复了，所以可以这样简化。

90.钢条切割问题：自顶向下实现

对照上面的公式写出以下两种实现，第二种简化的方法，少了一次递归，时间上少了很多。

将p改成p = [0,1,5,8,9,10,17,17,20,24,30,31,33,35,36,40,41,42,45,46,50]，长度改大，计算最大的时间也变慢了。

因为递归算法由于重复求解相同子问题，效率极低，随着长度越大，求解速度会变慢

因为这是用了自顶向下递归实现，为何自顶向下递归的效率会这么差？
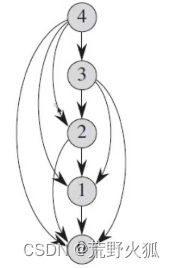
时间复杂度为O(2^n),如果n越大，就会造成指数爆炸。
求f(4),会重复求许多相同的问题。

动态规划的思想：每个问题只求解一次，保存求解结果
之后需要此问题时，只需要查找并保存结果。

91.钢条切割问题：自底向上实现

动态规划就是自底向上实现，每次都把最好的存起来，调用时直接取出来，不用再算。
按照第二种简化的方法写。

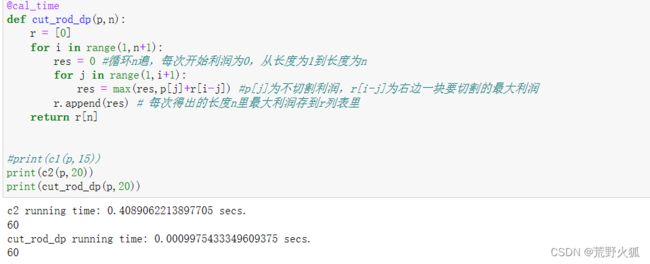
时间上比递归的方法快很多，时间复杂度为O(n^2)

92.钢条切割问题：重构解

如何修改动态规划算法，使其不仅输出最优解，还输出最优切割方案？
对每个问题，保存切割一次时左切切下的长度，s[i]为保存的当前最优利润时，左切下的长度

max()的话就不知道里面左边不切割的长度是多少，所以要换成以下写法

实际上这样把每次切出来的长度列出来，有个专有的名词叫路径带回

什么问题可以用动态规划方法？涉及到最大，最小，最优时

实际上，贪心算法是动态规划一个特例，贪心能解动态也能解，贪心不能解，动态也能解。
可以先从递归的思想想问题，如果递归能解就意味着动态规划能解。

93.最长公共子序列

首先要找到递推式或者说是最优子结构。
我们发现这样一个规律，如果两个字符串的最后一个字符不相等，比如说“ABCBDAB”和“BDCABA”这两个字符串找最长公共子序列。我们先看最后一个字符，不一样，那么我们可以等同于“ABCBDAB”和“BDCAB”中找最长公共子序列，或者“ABCBDA”和“BDCABA”中找，两者中哪个最长就是最长的公共子序列。如果最后一个字符一样，比如“ABCBDA”和“BDCABA”，那么最长的公共子序列就等于“ABCBD”和“BDCAB”的最长公共子序列 +1(因为最后一个字符相等)。
就得出如下定理：

安照这个图得出，空字符时都为0，如果末尾字符相等，那就取上面格子和下面格子的最大值，如果不相等，就取左上角一个格子的值+1。（从左上角过来的值代表匹配）

最长公共子序列：实现

首先求最长公共子序列的长度

再利用回溯法得出，这个最长的子序列的字符是多少

这种做法只能求得一个，如果 elif c[i-1][j] > c[i][j-1]: 改成 >= 则答案是BCBA，这两个都是最长公共子序列，所以都是对的。
存的路径如下。

总结

学习了动态规划算法。

---