NLP Beginner 任务一：基于机器学习的文本分类

NlP Beginner系列文章目录

任务一：基于机器学习的文本分类

---

前言

前两周每天一章的进度看完了鱼书《深度学习进阶：自然语言处理》，苦于没有实战项目练手。复旦大学邱锡鹏老师的NLP-Beginner：自然语言处理入门练习，感觉不错。练习共有五个任务，计划在三周内能够完成。

这里提示一下，任务的参考书籍是邱老师的《神经网络与深度学习》一书。以任务一为例，我在阅读了此书前两章后，才着手任务一。但是由于我个人的情况是此前已经学习过李宏毅深度学习和一些机器学习入门项目，急需的是项目练手。但是此书内容全面充实，理论偏多，代码偏少，不适合于我现阶段的需求。并且对于任务的完成而言，除了3.3节softmax公式的推导，其余内容对任务的完成帮助不大。所以建议有一定基础的同学，直接上手任务，对书中的内容有选择的进行针对性阅读。

此外，个人强烈推荐先看《深度学习进阶：自然语言处理》，以此书为基础，在了解了自然语言处理的大概内容及其代码实现后，再针对项目中的实际问题进行针对性训练。本文也会对书中的相关内容进行复习。

这里特别鸣谢
  NLP-Beginner 任务一：基于机器学习的文本分类 博客，本文在学习此篇博客的基础上，加入了一些自己的理解，更正与扩充。

---

一、任务介绍

本任务要求基于logistic/softmax regression实现文本分类。

任务背景来源于kaggle的一个比赛 Sentiment Analysis on Movie Reviews，利用数据集The Rotten Tomatoes movie review dataset ，将每个句子分为五类情感：negetive,somewhat negetive,neutral,somewhat positive,positive中的一类，分别用标签 0、1、2、3、4表示。

数据集下载：（迅雷链接：https://pan.xunlei.com/s/VNGUL-OUi9-ZS-IeayC2GnhVA1?pwd=7ccz#）
提取码：7ccz 复制这段内容后打开手机迅雷App，查看更方便）

二、文本特征表示

1.词袋模型（Bag of word）

词袋模型即把句子是由单词组成的无需集合。对于每个位置，单词出现则为1，不出现则为0.

例子：

单词：i,you,him,her,love,hate,but

句子A:I love you                                      向量A   :[1,1,0,0,1,0,0]

句子B:love you but hate him                   向量B   :[1,1,1,0,1,1,1]

句子C:I hate you but love him                 向量C   :[1,1,1,0,1,1,1]

这种转换方式很简单，但是由于没有考虑词序问题，句子B和句子C两个意思不一样的句子，向量确实一样的。因此，词袋模型在这种情况下会存在比较大的缺陷。

2.N元特征（N gram）

N元特征（N-gram），是由N个字或词组成的字符串。以N为2时，二元特征为例，“机器学习算法”以字为基本单位的二元特征集合为：{机器，器学，学习，习算，算法}。集合中每一项都是由二个相邻的字组成的子串，长度为2。这些子串可以是有益的（如：学习），也可以是无意义的（如：器学）。但是这些无意义的子串也有可能在分类中起到很关键的作用。一个长度为L的句子，可以提取出L-1个二元特征。

随着N的增加，可以抽取的特征就会越多，特征空间也会指数增加。这些高阶的特征出现的频率也会相对降低，对分类不但没有太多帮助，还会直接影响后续的效率与复杂度。因此在一般的文本分类任务中，N取3就够了，并且同时也使用一元和二元特征，防止出现过拟合。

3.从概率角度理解N gram

概率语言模型

假设词串W = w1,w2,...,wn,以p(W)表示该词串可能出现的概率，那么从概率的角度上，

p(W) = p(w1,w2,...,wn)

要计算p(W)，根据链式法则有：

p(W)=p(w1)p(w2|w1)...p(wn|w1,w2,...,wn-1)

其中w1,w2,...,wi-1为第i个词的历史词

例句： likely connects audiences with content

p( likely connects audiences with content)

=p(likely|sentence starts)

*p(connects|likely)

*p(audiences|likely,connects)

*p(with|likely,connects,audiences)

*p(content|likely,connects,audience,with)

极大似然估计 

最简单的方式就是采用极大似然估计（Maximum Likelihood Estimation,MLE）

 例如，采用MLE估计：

p(content|likely,connects,audience,with) = C(likely connects audience with content)/

C(likely connects audience with)

该估计方法依赖于假设：当前词出现的概率依赖于前面的词。然而，如果前面词的个数很大，一方面语料库中C(w1,w2...wm)或C(w1,w2,...,wm-1)极有可能为0，就导致条件概率为0或者无法计算。另一方面，随着历史长度的增长，不同历史书目会按指数级增长。

在此基础上，提出一个可行方案：当前词仅依赖于较短的历史词。

马尔科夫假设

位于某个特定状态的概率取决于前n-1个状态，即n-1阶马尔科夫链

马尔科夫假设应用于语言模型：假设每个词的出现概率只取决于前n-1个词。

p(wi|w1,w2,...,wi-1) ≈ p(wi|wi-n+1,...,wi-1) 

这种语言模型也被称为N-gram模型。

N-gram模型

• 1-gram模型（unigram）
• p（w1,w2,...,wn）≈p(w1)p(w2)p(w3)...p(wn)
• 2-gram模型(bigram)
• p(w1,w2,..,wn)≈p(w1)p(w2|w1)p(w3|w2)...p(wn|wn-1)
• 3-gram模型(trigram)
• p(w1,w2,...,wn)≈p(w1)p(w2|w1)p(w3|w1,w2)...p(wn|wn-2,wn-1)

三、最优化求解

四、代码及实现

主文件-main.py

import numpy
import csv
import random
from feature import Bag,Gram
from comparison_plot import alpha_gradient_plot

with open('train.tsv') as f:
    tsvreader = csv.reader(f,delimiter='\t')
    temp = list(tsvreader)

data = temp[1:]
max_item = 1000
random.seed(2021)
numpy.random.seed(2021)

bag = Bag(data,max_item)
bag.get_words()
bag.get_matrix()

gram = Gram(data,dimension=2,max_item=max_item)
gram.get_words()
gram.get_matrix()

alpha_gradient_plot(bag,gram,10000,10)

特征提取 feature.py 

这里实现了

1. 训练集和测试集划分函数data_split()，利用随机函数random.random()生成(0,1)之间的数，并和test_rate进行比较，实现以test_rate为测试集占比的划分。
2. 词袋模型的Bag类和N gram的Gram类。两个类都由三个函数组成：init()初始化函数，定义用到的所有类中全局变量；get_words()遍历每句话中的每个词，得到全文中所有单词到单词编号的映射;get_matrix()得到训练集矩阵和测试集矩阵。
3. 对于每句话words中的每个单词word,如果word没在dict_words中，则把它加入字典的键，同时将其值赋为字典的长度；这样随着新词加入，字典长度增加0,1,2...，新词对应的值也相应增大。
4. get_words()依次取出data中的每个记录，对记录term进行操作；get_matrix()依次取出data中每个记录对应的编号i，对编号进行操作（为了方便于矩阵索引）

#特征提取
import numpy as np
import random

def data_split(data,test_rate=0.3,max_item=1000):
    """把数据按一定比例分成训练集和测试集"""
    train = list()
    test = list()
    i = 0
    for datum in data:
        i += 1
        if random.random() >test_rate:
            train.append(datum)
        else:
            test.append(datum)
        if i>max_item:
            break
    return train,test

class Bag:
    """Bag of words"""
    def __init__(self,my_data,max_item):
        self.data = my_data[:max_item]
        self.max_item = max_item
        self.dict_words = dict()    #单词到单词编号的映射
        self.len = 0                #单词数量
        self.train,self.test = data_split(my_data,test_rate=0.3,max_item=1000)  #划分训练集测试集
        self.train_y = [int(term[3]) for term in self.train]    #训练集标签
        self.test_y = [int(term[3]) for term in self.test]      #测试集标签
        self.train_matrix = None    #训练集的0-1矩阵（每行一个句子）
        self.test_matrix = None     #测试集的0-1矩阵（每行一个句子）

    def get_words(self):
        for term in self.data:
            s = term[2]
            s = s.upper()   #统一转化为大写（或者全部转化为小写，否则I和i会被识别为两个不同的单词）
            words = s.split()
            for word in words:
                if word not in self.dict_words: #判断此单词是否出现过，如果没有则加入字典
                    self.dict_words[word] = len(self.dict_words)    #单词加入字典后，字典长度增加，则下一个单词的编号也增加
        self.len = len(self.dict_words)
        self.test_matrix = np.zeros((len(self.test),self.len))   #初始化0-1矩阵
        self.train_matrix = np.zeros((len(self.train),self.len))

    def get_matrix(self):
        for i in range(len(self.train)):    #训练集矩阵
            s = self.train[i][2]
            words = s.split()
            for word in words:
                word = word.upper()
                self.train_matrix[i][self.dict_words[word]]=1
        for i in range(len(self.test)):     #测试集矩阵
            s = self.test[i][2]
            words = s.split()
            for word in words:
                word = word.upper()
                self.test_matrix[i][self.dict_words[word]]=1

class Gram:
    """N-gram"""
    def __init__(self,my_data,dimension=2,max_item=1000):
        self.data = my_data[:max_item]
        self.max_item = max_item
        self.dict_words = dict()    #特征到编号的映射
        self.len = 0                #特征数量
        self.dimension = dimension  #使用几元特征，1-gram,2-gram...
        self.train,self.test = data_split(my_data,test_rate=0.3,max_item=max_item)
        self.train_y = [int(term[3]) for term in self.train]  #训练集类别
        self.test_y =[int(term[3]) for term in self.test]
        self.train_matrix = None                    #训练集0-1矩阵（每行代表一句话）
        self.test_matrix = None

    def get_words(self):
        for d in range(1,self.dimension+1):          #提取1-gram,2-gram...N-gram特征
            for term in self.data:
                s = term[2]
                s = s.upper()
                words = s.split()
                for i in range(len(words)-d+1): #一个一个遍历d-gram下的每一个特征
                    temp = words[i:i+d]
                    temp = '_'.join(temp)       #形成i d-gram 特征
                    if temp not in self.dict_words:
                        self.dict_words[temp] = len(self.dict_words)
        self.len = len(self.dict_words)
        self.train_matrix = np.zeros((len(self.train),self.len))  #训练集矩阵初始化
        self.test_matrix = np.zeros((len(self.test),self.len))

    def get_matrix(self):
        for d in range(1,self.dimension+1):
            for i in range(len(self.train)):    #训练集矩阵
                s = self.train[i][2]
                s = s.upper()
                words = s.split()

                for j in range(len(words)-d+1):
                    temp = words[j:j+d]
                    temp = '_'.join(temp)
                    self.train_matrix[i][self.dict_words[temp]] = 1

            for i in range(len(self.test)):     #测试集矩阵
                s = self.test[i][2]
                s = s.upper()
                words = s.split()

                for j in range(len(words)-d+1):
                    temp = words[j:j+d]
                    temp = '_'.join(temp)
                    self.test_matrix[i][self.dict_words[temp]] = 1

Softmax回归- mysoftmax_regression.py

这里有两个函数重点讲解一下，change_y()把情感种类转化为一个one-hot向量，这里是把有y[k]转化为one-hot向量；regression()针对"mini"、"shuffle"、"batch"三种策略进行选择处理，每种策略中都对权重self.W进行times次更新。

代码中也有两处地方没太理解，一是prediction()中，既然返回的是最大值下标，那么为什么还需要经过sofmax的归一化，直接使用x.dot(self.W)的结果可以哇。二是regression()中，对样本长度进行条件判断时，x和y不应该是一样长的吗。

import numpy as np
import random

class Softmax:
    """softmax regression"""
    def __init__(self,sample,typenum,feature):
        self.sample = sample    #训练集样本个数
        self.typenum = typenum  #情感种类
        self.feature = feature  #dict_words向量的长度
        self.W = np.random.randn(feature,typenum) #参数矩阵W初始化

    def softmax_calculation(self,x):
        """x是向量，计算softmax值"""
        exp = np.exp(x-np.max(x))   #先减去行最大值防止指数太大溢出
        return exp/exp.sum()

    def softmax_all(self,wtx):
        """wtx是矩阵，即许多向量叠在一起，按行计算softmax的值"""
        wtx -= np.max(wtx,axis=1,keepdims=True)
        wtx = np.exp(wtx)
        wtx = wtx/np.sum(wtx,axis=1,keepdims=True)
        return wtx

    def change_y(self,y):
        """把情感种类转化为一个one-hot向量"""
        ans = np.array([0]*self.typenum)
        # print("{}".format(y))
        ans[y] = 1
        return ans.reshape(-1,1)

    def prediction(self,x):
        """给定0-1矩阵X，计算每个句子的y_hat值（概率）"""
        prob = self.softmax_all(x.dot(self.W))
        return prob.argmax(axis=1)           #既然返回的是最大值，那为什么要需要经过softmax,直接返回 x.dot(self.W)的最大值也可以哇

    def correct_rate(self,train,train_y,test,test_y):
        """计算训练集和测试集的准确率"""
        #train set
        n_train = len(train)
        pred_train = self.prediction(train)
        train_correct = sum(train_y[i] == pred_train[i] for i in range(n_train)) / n_train
        #test set
        n_test = len(test)
        pred_test = self.prediction(test)
        test_correct = sum(test_y[i] == pred_test[i] for i in range(n_test)) / n_test

        print("train_correct:{}   test_correct:{}".format(train_correct,test_correct))
        return train_correct,test_correct

    def regression(self,x,y,alpha,times,strategy="mini",mini_size=100):
        """Softmax regression"""
        if self.sample != len(x) or self.sample != len(y):    #这里x 和 y不应该一样长吗
            raise Exception("Sample size does not match!")
        #mini-batch
        if strategy == "mini":
            for i in range(times):
                increment = np.zeros((self.feature,self.typenum))
                for i in range(mini_size):                  #随机抽mini-size次
                    k = random.randint(0,self.sample-1)
                    y_hat = self.softmax_calculation(self.W.T.dot(x[k].reshape(-1,1)))
                    increment += x[k].reshape(-1,1).dot((self.change_y(int(y[k]))-y_hat).T)     #梯度加和
                self.W += alpha/mini_size*increment         #参数更新
        #shuffle 随机梯度
        elif strategy == "shuffle":
            for i in range(times):
                k = random.randint(0,self.sample-1)     #每次抽一个
                y_hat = self.softmax_calculation(self.W.T.dot(x[k].reshape(-1,1)))
                # print("y[{}]:{}".format(k,y[k]))
                # print("y_hat:{}".format(y_hat))
                increment = x[k].reshape(-1,1).dot((self.change_y(int(y[k]))-y_hat).T)      #计算梯度

                self.W += alpha*increment   #参数更新

        #batch 整批量梯度
        elif strategy == "batch":
            for i in range(times):
                increment = np.zeros((self.feature,self.typenum))
                for i in range(self.sample):    #所有样本都要计算
                    k = random.randint(0,self.sample-1)
                    y_hat = self.softmax_calculation(self.W.T.dot(x[k].reshape(-1,1)))
                    increment += x[k].reshape(-1,1).dot((self.change_y(int(y[k]))-y_hat).T)     #梯度加和
                self.W += alpha*increment/self.sample   #参数更新

        else:
            raise Exception("Unkown strategy")

结果&画图-comparison_plot.py

import matplotlib.pyplot as plt
from mysoftmax_regression import Softmax

def alpha_gradient_plot(bag,gram,total_times,mini_size):
    """Plot categorization verses different parameters"""
    alphas = [0.001,0.01,0.1,1,10,100,1000,10000]

    #Bag of words

    #Shuffle
    shuffle_train = list()
    shuffle_test = list()
    for alpha in alphas:
        soft = Softmax(len(bag.train),5,bag.len)
        soft.regression(bag.train_matrix,bag.train_y,alpha,total_times,"shuffle")
        r_train,r_test = soft.correct_rate(bag.train_matrix,bag.train_y,bag.test_matrix,bag.test_y)
        shuffle_train.append(r_train)
        shuffle_test.append(r_test)

    #Batch
    batch_train = list()
    batch_test = list()
    for alpha in alphas:
        soft = Softmax(len(bag.train), 5, bag.len)
        soft.regression(bag.train_matrix, bag.train_y, alpha, int(total_times/bag.max_item), "batch")
        r_train, r_test = soft.correct_rate(bag.train_matrix, bag.train_y, bag.test_matrix, bag.test_y)
        batch_train.append(r_train)
        batch_test.append(r_test)

    #Mini-batch
    mini_train = list()
    mini_test = list()
    for alpha in alphas:
        soft = Softmax(len(bag.train), 5, bag.len)
        soft.regression(bag.train_matrix, bag.train_y, alpha, total_times, "mini")
        r_train, r_test = soft.correct_rate(bag.train_matrix, bag.train_y, bag.test_matrix, bag.test_y)
        mini_train.append(r_train)
        mini_test.append(r_test)

    plt.subplot(2, 2, 1)
    plt.semilogx(alphas, shuffle_train, 'r--', label='shuffle')
    plt.semilogx(alphas, batch_train, 'g--', label='batch')
    plt.semilogx(alphas, mini_train, 'b--', label='mini-batch')
    plt.semilogx(alphas, shuffle_train, 'ro-', alphas, batch_train, 'g+-', alphas, mini_train, 'b^-')
    plt.legend()
    plt.title("Bag of words -- Training Set")
    plt.xlabel("Learning Rate")
    plt.ylabel("Accuracy")
    plt.ylim(0, 1)
    plt.subplot(2, 2, 2)
    plt.semilogx(alphas, shuffle_test, 'r--', label='shuffle')
    plt.semilogx(alphas, batch_test, 'g--', label='batch')
    plt.semilogx(alphas, mini_test, 'b--', label='mini-batch')
    plt.semilogx(alphas, shuffle_test, 'ro-', alphas, batch_test, 'g+-', alphas, mini_test, 'b^-')
    plt.legend()
    plt.title("Bag of words -- Test Set")
    plt.xlabel("Learning Rate")
    plt.ylabel("Accuracy")
    plt.ylim(0, 1)

    # N-gram
    # Shuffle
    shuffle_train = list()
    shuffle_test = list()
    for alpha in alphas:
        soft = Softmax(len(gram.train), 5, gram.len)
        soft.regression(gram.train_matrix, gram.train_y, alpha, total_times, "shuffle")
        r_train, r_test = soft.correct_rate(gram.train_matrix, gram.train_y, gram.test_matrix, gram.test_y)
        shuffle_train.append(r_train)
        shuffle_test.append(r_test)

    # Batch
    batch_train = list()
    batch_test = list()
    for alpha in alphas:
        soft = Softmax(len(gram.train), 5, gram.len)
        soft.regression(gram.train_matrix, gram.train_y, alpha, int(total_times / gram.max_item), "batch")
        r_train, r_test = soft.correct_rate(gram.train_matrix, gram.train_y, gram.test_matrix, gram.test_y)
        batch_train.append(r_train)
        batch_test.append(r_test)

    # Mini-batch
    mini_train = list()
    mini_test = list()
    for alpha in alphas:
        soft = Softmax(len(gram.train), 5, gram.len)
        soft.regression(gram.train_matrix, gram.train_y, alpha, int(total_times / mini_size), "mini", mini_size)
        r_train, r_test = soft.correct_rate(gram.train_matrix, gram.train_y, gram.test_matrix, gram.test_y)
        mini_train.append(r_train)
        mini_test.append(r_test)
    plt.subplot(2, 2, 3)
    plt.semilogx(alphas, shuffle_train, 'r--', label='shuffle')
    plt.semilogx(alphas, batch_train, 'g--', label='batch')
    plt.semilogx(alphas, mini_train, 'b--', label='mini-batch')
    plt.semilogx(alphas, shuffle_train, 'ro-', alphas, batch_train, 'g+-', alphas, mini_train, 'b^-')
    plt.legend()
    plt.title("N-gram -- Training Set")
    plt.xlabel("Learning Rate")
    plt.ylabel("Accuracy")
    plt.ylim(0, 1)
    plt.subplot(2, 2, 4)
    plt.semilogx(alphas, shuffle_test, 'r--', label='shuffle')
    plt.semilogx(alphas, batch_test, 'g--', label='batch')
    plt.semilogx(alphas, mini_test, 'b--', label='mini-batch')
    plt.semilogx(alphas, shuffle_test, 'ro-', alphas, batch_test, 'g+-', alphas, mini_test, 'b^-')
    plt.legend()
    plt.title("N-gram -- Test Set")
    plt.xlabel("Learning Rate")
    plt.ylabel("Accuracy")
    plt.ylim(0, 1)
    plt.tight_layout()
    plt.show()

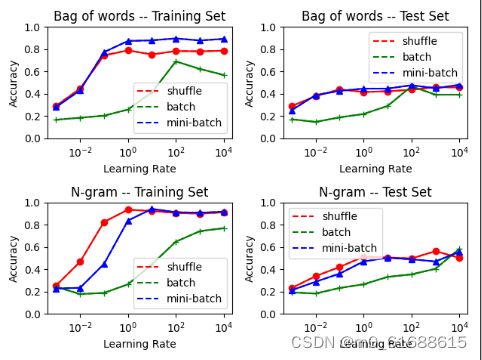
 结果

从横轴看来，小的学习率不足以让模型收敛，这里大学习率效果更好，且未发生振荡现象。shuffle和mini-batch明显优于batch。测试集上情况和训练集类似。

基于以上图片，我们可以得出下述结论：使用N gram在学习率为1左右，对于本数据集的Softmax回归模型参数求解效果最佳。

---

总结

除了画图部分，其余部分都自己进行了理解实现，再调试跑通结果之后，自己再独立对项目进行复现。在任务原有的要求中，还有损失函数以及特征选择部分没有进行效果测试，希望之后有机会进行扩充。