java实现,二叉搜索树(过程非常详细)
文章目录
-
- 1. 接口设计
- 2. 添加步骤
- 3. 比较规则定义
-
- 3.1 第一种:定义一个比较接口(给类添加比较规则)
- 3.2 第二种:定义一个比较器(给集合添加比较规则)
- 3.3 最终解决方案
- 4. 遍历二叉搜索树
-
- 4.1 前序遍历
-
- 4.1.1 递归实现
- 4.1.2 非递归、迭代实现(使用栈实现)
- 4.2 中序遍历
-
- 4.2.1 递归实现
- 4.2.2 非递归(栈实现)
- 4.3 后序遍历
-
- 4.3.1 递归实现
- 4.3.2 非递归(栈实现)
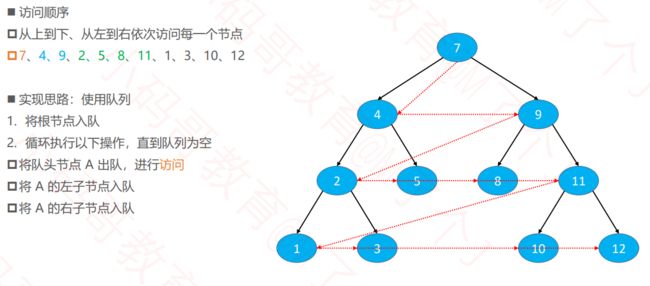
- 4.4 层序遍历
-
- 4.4.1 队列实现层序遍历
- 4.5 LeetCode对应练习
- 5. 设计对外遍历暴露的接口
-
- 5.1 设计对外遍历暴露的接口
- 5.2 增强对外遍历暴露的接口
- 6. 各种遍历的应用
- 7. 前驱结点、后继结点
- 8. remove方法实现
-
- 8.1 删除的是叶子结点
- 8.2 删除的是度为一的结点
- 8.3 删除的是度为二的结点
- 8.4 代码实现
- 9. 设计继承结构,重构BST
思维导图:
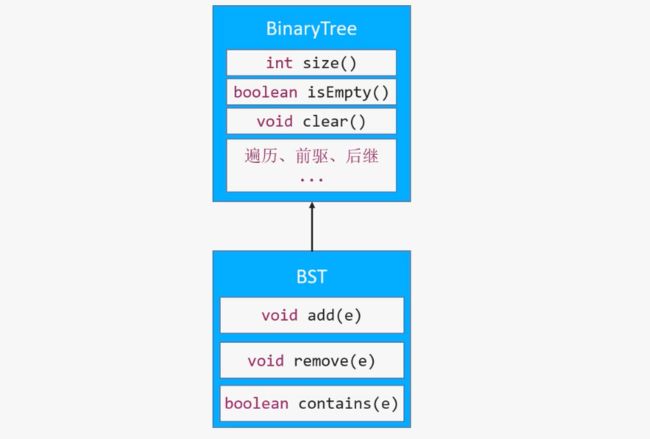
1. 接口设计
int size();//元素的数量
boolean isEmpty();//是否为空
void clear();//清除所有的元素
void add(E element);//添加元素
void remove(E element);//删除元素
boolean contains();//是否包含某元素
2. 添加步骤
- 找到父结点parent
- 创建新结点node
- parent.left = node 或者 parent.right= node
- 遇到值相同的直接返回或者覆盖该元素(推荐覆盖该元素,因为比较的可能是对象,对象中的某个值相等的话需要覆盖)
3. 比较规则定义
在二叉搜索树中,有一个非常重要的特性,就是二叉搜索树存储的元素必须具备可比性,不允许为null。如果传入的是一个类我们必须要指定比较的规则,我们需要告诉保存我们类的集合什么是大,什么是小,在Java中一般我们有两种做法
3.1 第一种:定义一个比较接口(给类添加比较规则)
public interface Comparable<E> {
int compareTo(E e);//定义比较规则
}
然后每个需要比较的对象都必须要实现这个比较接口并且需要指定比较规则,例如我这里定义一个Person对象
public class Person implements Comparable<Person>{
private int age;
public Person(int age){
this.age = age;
}
public int getAge(){
return age;
}
/**
* 比较规则,我们可以指定返回值大于1表示当前类在比较中是大的,小于0表示是小的,0表示相等
*/
@Override
public int compareTo(Person person) {
// if(age > person.age) return 1; //可以简化成下面的写法
// if(age < person.age) return -1;
// return 0;
return age - person.age;
}
}
这种比较规则的缺点也显而易见,就是比较规则都写在待比较的类里面了,不够灵活,如果我们对两个集合的比较规则不一样的话就不能进行合适的比较了。例如想在我有两个Person集合同时进行比较,第一个集合的比较规则是年纪大的大,而第二个集合比较规则是年纪小的大,这样的话就不能同时进行比较。
3.2 第二种:定义一个比较器(给集合添加比较规则)
我们可以指定一个比较器,并当做参数传入到集合BinarySearchTree中
/**
* 比较器,可以在类外面自定义比较规则,这种方式是给集合指定比较规则
* @param
*/
public interface Comparator<E> {
int compare(E e1,E e2);
}
我们在BinarySearchTree中通过构造器就可以将我们自定义的比较规则传入
private Comparator<E> comparator;//比较器
public BinarySearchTree(Comparator<E> comparator){this.comparator = comparator;}
然后就可以非常灵活的每次创建集合的时候都指定比较规则,也不用每个类都去实现Comparable接口了
/**
* 自定义比较规则1
*/
private static class PersonComparator implements Comparator<Person>{
@Override
public int compare(Person e1, Person e2) {
return e1.getAge() - e2.getAge();
}
}
/**
* 自定义比较规则2
*/
private static class PersonComparator2 implements Comparator<Person>{
@Override
public int compare(Person e1, Person e2) {
return e2.getAge() - e1.getAge();
}
}
@Test
public void test01(){
BinarySearchTree<Person> bst1 = new BinarySearchTree<>(new PersonComparator());
bst1.add(new Person(11));
bst1.add(new Person(12));
BinarySearchTree<Person> bst2 = new BinarySearchTree<>(new PersonComparator2());
bst2.add(new Person(11));
bst2.add(new Person(12));
}
当然我们也可以通过匿名内部类进行简化
@Test
public void test01(){
BinarySearchTree<Person> bst1 = new BinarySearchTree<>(new Comparator<Person>() {
@Override
public int compare(Person e1, Person e2) {
return e1.getAge() - e2.getAge();
}
});
bst1.add(new Person(11));
bst1.add(new Person(12));
BinarySearchTree<Person> bst2 = new BinarySearchTree<>(new Comparator<Person>() {
@Override
public int compare(Person e1, Person e2) {
return e2.getAge() - e1.getAge();
}
});
bst2.add(new Person(11));
bst2.add(new Person(12));
}
不过我们一般开发都是会使用Lambda语法进行进一步的简化
@Test
public void test01(){
BinarySearchTree<Person> bst1 = new BinarySearchTree<>((e1, e2) -> e1.getAge() - e2.getAge());
bst1.add(new Person(11));
bst1.add(new Person(12));
BinarySearchTree<Person> bst2 = new BinarySearchTree<>((e1, e2) -> e2.getAge() - e1.getAge());
bst2.add(new Person(11));
bst2.add(new Person(12));
}
这两种方式都很常见,第一种方法我们在给List进行排序的时候经常用到Collections.sort()对其进行排序,只需要在需要排序的类E中实现java.lang.Comparable比较接口就可以了,比较规则也是在每一次的比较中返回大于1的数表示当前类大,返回小于0的数表示当前类小,返回0表示一样大。当然list本身自己也有sort()方法用来对其中的对象进行排序
通过Collections.sort()的方式
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
Collections.sort(list,Person::compareTo);
list.forEach(e -> System.out.println(e.getAge()));
}
通过list.sort()进行排序
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
list.sort(Person::compareTo);
list.forEach(e -> System.out.println(e.getAge()));
}
还可以用stream API
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
list.stream()
.sorted()
.forEach(e -> System.out.println(e.getAge()));
}
第二种方式使用Comparator比较器,给每一个集合定制比较规则,其实这种方式更加常用,一般开发中我们都是用的这种方法,给集合定制比较规则,而不是去给类实现比较接口
通过Collections.sort()的方式
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
Collections.sort(list, new java.util.Comparator<Person>() {
@Override
public int compare(Person o1, Person o2) {
return o2.getAge() - o1.getAge();
}
});
}
//Lambda简化
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
Collections.sort(list, (o1, o2) -> o2.getAge() - o1.getAge());
}
通过list.sort()进行排序
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
list.sort(new java.util.Comparator<Person>() {
@Override
public int compare(Person o1, Person o2) {
return o1.getAge() - o2.getAge();
}
});
}
//Lambda简化
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
list.sort((o1, o2) -> o2.getAge() - o1.getAge());
}
stream API
@Test
public void test02(){
List<Person> list = new ArrayList<>();
list.add(new Person(20));
list.add(new Person(19));
list.stream()
.sorted((o1, o2) -> o2.getAge() - o1.getAge())
.forEach(e -> System.out.println(e.getAge()));
}
3.3 最终解决方案
第一种方法让类去实现Comparable并自定义compareTo方法不够灵活,无法对每个集合对定制比较规则
第二种方法比较灵活,但是每次都需要传入比较器
综上所述:我们可以结合两者使用,我们可以传入给集合定制的比较器,也可以不传,不传就默认使用类实现比较接口的比较器,但是如果我们在集合中写成这样的话其实也有问题,就是待比较的类我们都必须实现比较接口,不实现就报错
public class BinarySearchTree<E extends Comparable<E>> {}
为了解决这个问题,我们可以在集合中具体的比较中这样写,这样的话既不用强制让类实现比较接口,又不用强制给集合传入比较器,当然Java其实已经实现了comparator和Comparable
/**
* 规定传入对象的比较规则
* @param e1 第一个对象
* @param e2 第二个对象
* @return 0表示相等,大于0表示 e1 > e2,小于0表示 e2 < e1
*/
@SuppressWarnings("unchecked")//表示不进行强制类型转换提示,即下面类型转换的时候没有类型装换提示
private int compare(E e1,E e2){
if(comparator != null){
return comparator.compare(e1,e2);
}
return ((Comparable<E>) e1).compareTo(e2);
}
贴一下实现了部分功能的代码,可以实现比较和插入
package com.fx.binarySearchTree;
import com.fx.printer.BinaryTreeInfo;
import java.util.Stack;
/**
* @author: Eureka
* @date: 2022/3/14 20:12
* Description: 二叉搜索树
*/
@SuppressWarnings("unchecked")
public class BinarySearchTree<E> implements BinaryTreeInfo {
//结点以内部类的形式存在
private static class Node<E> {
E element;//当前结点保存的元素
Node<E> left;//左结点
Node<E> right;//右结点
Node<E> parent;//父结点
public Node(E element, Node<E> parent) {
this.element = element;
this.parent = parent;
}
}
private int size;//当前树结点个数
private Node<E> root;//根结点
private Comparator<E> comparator;//比较器
public BinarySearchTree() {
}
public BinarySearchTree(Comparator<E> comparator) {
this.comparator = comparator;
}
public void add(E element) {
//非空检测
elementNotNullCheck(element);
//先判断是否为根结点
if (root == null) {
root = new Node<>(element, null);
}
//非根结点,非递归进行添加
Node<E> node = root;//用来标记移动的结点
Node<E> parent = root;//保存当前结点的父结点,默认根结点就是父结点
//根据比较规则找到待添加元素的位置
int cmp = 0;
while (node != null) {
//比较值
cmp = compare(element, node.element);
//保存当前结点的父结点
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else {
return;
}
}
//添加元素
Node<E> newNode = new Node<>(element, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
}
public void remove(E element) {
}
public boolean contains(E e1, E e2) {
return true;
}
/**
* 规定传入对象的比较规则
*
* @param e1 第一个对象
* @param e2 第二个对象
* @return 0表示相等,大于0表示 e1 > e2,小于0表示 e2 < e1
*/
private int compare(E e1, E e2) {
if (comparator != null) {
return comparator.compare(e1, e2);
}
//这样装换可以不用强制要求类实现Comparable接口
return ((java.lang.Comparable<E>) e1).compareTo(e2);
}
/**
* 返回树结点个数
*/
public int size() {
return size;
}
/**
* 判断树是否为空
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 清空当前树
*/
public void clear() {
}
/**
* 判断元素是否为空
*/
private void elementNotNullCheck(E element) {
if (element == null) {
throw new IllegalArgumentException("element must not be null");
}
}
}
4. 遍历二叉搜索树
一共有四种遍历方式:
前序遍历(Preorder Traversal)
中序遍历(Inorder Traversal)
后续遍历(Postorder Traversal)
层序遍历(Level Order Traversal)
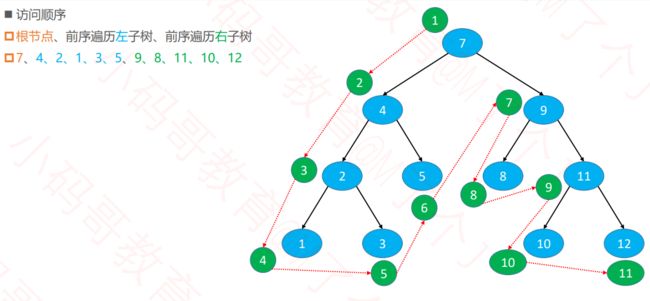
4.1 前序遍历
其实我在记这些遍历的时候更喜欢记为前根遍历、中根遍历、后根遍历,对应着遍历的分别是,当然也对应一些方法
前根遍历 --> 根左右 --> 包线法
中根遍历 --> 左根右
后根遍历 --> 左右根
前根遍历,就是先遍历根结点,然后左子树,右子树,举个栗子:
4.1.1 递归实现
/**
* 前序遍历
*/
public void preorderTraversal(){
preorderTraversal(root);
}
public void preorderTraversal(Node<E> node){
if(node == null) return;
//业务代码
System.out.println(node.element);
preorderTraversal(node.left);
preorderTraversal(node.right);
}
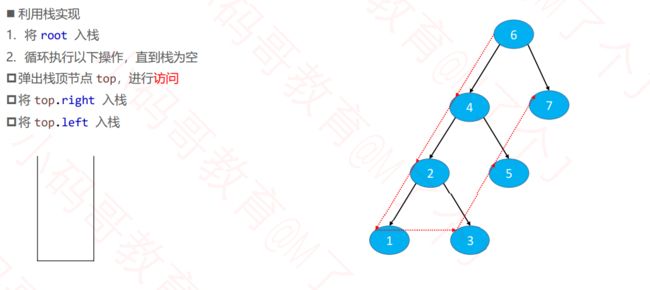
4.1.2 非递归、迭代实现(使用栈实现)
代码实现:
private final Stack<Node<E>> stack = new Stack<>();
public void preorderTraversalByStack(){
//将根元素入栈
preorderTraversalByStack(root);
}
public void preorderTraversalByStack(Node<E> popNode){
while (popNode != null){
//输出元素
System.out.println(popNode.element);
//将其右结点入栈
if(popNode.right != null){
stack.push(popNode.right);
}
//将其左结点入栈
if(popNode.left != null){
stack.push(popNode.left);
}
//将栈顶元素出栈
popNode = stack.isEmpty() ? null : stack.pop();
}
}
4.2 中序遍历
中序遍历,根结点在中间,例如左根右、右根左,举个栗子:
4.2.1 递归实现
/**
* 中序遍历(递归实现)
*/
public void inorderTraversal(){
inorderTraversal(root);
}
public void inorderTraversal(Node<E> node){
if(node == null) return;
inorderTraversal(node.left);
System.out.println(node.element);
inorderTraversal(node.right);
}
如果想要降序只需要改变一下递归的顺序
public void inorderTraversal(Node<E> node){
if(node == null) return;
inorderTraversal(node.right);
System.out.println(node.element);
inorderTraversal(node.left);
}
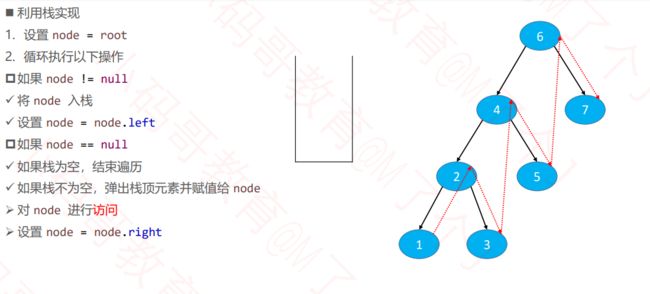
4.2.2 非递归(栈实现)
public void inorderTraversalByStack() {
inorderTraversalByStack(root);
}
public void inorderTraversalByStack(Node<E> popNode) {
//只要左结点存在就一直入栈
while (true) {
if(popNode != null){
stack.push(popNode);
popNode = popNode.left;
}else {
if(stack.isEmpty()) return;
popNode = stack.pop();
//业务逻辑
System.out.println(popNode.element);
popNode = popNode.right;
}
}
}
4.3 后序遍历
4.3.1 递归实现
public void postorderTraversal() {
postorderTraversal(root);
}
public void postorderTraversal(Node<E> node) {
if (node == null) return;
postorderTraversal(node.left);
postorderTraversal(node.right);
System.out.println(node.element);
}
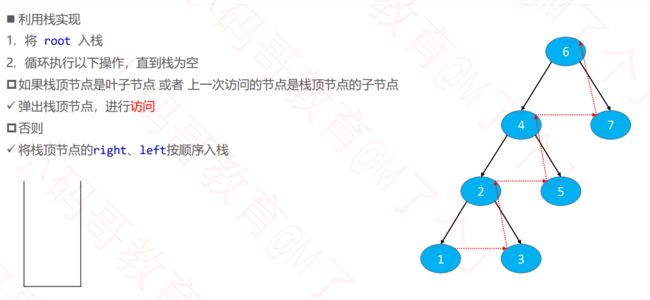
4.3.2 非递归(栈实现)
public void postorderTraversalByStack(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode temp = null;
while (!stack.isEmpty()) {
temp = stack.pop();
//业务逻辑
System.out.println(temp);
if (temp.left != null) {
stack.push(temp.left);
}
if (temp.right != null) {
stack.push(temp.right);
}
}
}
4.4 层序遍历
4.4.1 队列实现层序遍历
由于层序遍历的性质,显然递归是无法实现的,所以最好采用队列进行实现
public void leverOrderTraversal(){
if(root == null) return;
Queue<Node<E>> queue = new LinkedList<>();
//将根结点入队
queue.offer(root);
while (!queue.isEmpty()){
//出队
Node<E> node = queue.poll();
System.out.print(node.element);
if(node.left !=null) queue.offer(node.left);
if(node.right !=null) queue.offer(node.right);
}
}
4.5 LeetCode对应练习
-
二叉树的前序遍历: https://leetcode-cn.com/problems/binary-tree-preorder-traversal/ (递归+迭代)
-
二叉树的中序遍历 : https://leetcode-cn.com/problems/binary-tree-inorder-traversal/ (递归+迭代)
-
二叉树的后序遍历: https://leetcode-cn.com/problems/binary-tree-postorder-traversal/ (递归+迭代)
-
二叉树的层次遍历: https://leetcode-cn.com/problems/binary-tree-level-order-traversal/ (迭代)
-
二叉树的最大深度: https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/ (递归+迭代)
-
二叉树的层次遍历II: https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/
-
二叉树最大宽度:https://leetcode-cn.com/problems/maximum-width-of-binary-tree/
-
N叉树的前序遍历: https://leetcode-cn.com/problems/n-ary-tree-preorder-traversal/
-
N叉树的后序遍历: https://leetcode-cn.com/problems/n-ary-tree-postorder-traversal/
-
N叉树的最大深度: https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
5. 设计对外遍历暴露的接口
5.1 设计对外遍历暴露的接口
在前面的四种遍历方式中,都只是把遍历到的元素打印了出来,但我们实际应用的业务场景可以并不是去打印遍历到的元素,可能实现想对遍历到的元素加一。所以我们对外暴露的遍历接口需要重写优化一下!
核心思想与之前比较规则定义的思路一样,让用户在遍历之前将对元素操作的逻辑传入到遍历的函数中
定义遍历的回调接口
//遍历接口,接口可以写在BST内部
public interface Visitor<E>{
void visit(E element);
}
修改一下前面的代码,将对遍历到元素的业务逻辑交给调用者传入
//层次遍历接口暴露
public void leverOrderTraversal(Visitor<E> visitor){
if(root == null || visitor == null){
throw new IllegalArgumentException("参数不合法");
}
Queue<Node<E>> queue = new LinkedList<>();
//将根结点入队
queue.offer(root);
while (!queue.isEmpty()){
//出队
Node<E> node = queue.poll();
//回调,将处理遍历数据的业务交给调用者
visitor.visit(node.element);
if(node.left !=null) queue.offer(node.left);
if(node.right !=null) queue.offer(node.right);
}
}
我们可以测试一下:
@Test
public void test03(){
int[] arr = new int[]{7,4,9,2,5,8,11,3};
BinarySearchTree<Integer> bst1 = new BinarySearchTree<>();
//将数据添加到BST中
Arrays.stream(arr).forEach(bst1::add);
bst1.leverOrderTraversal(new BinarySearchTree.Visitor<Integer>() {
@Override
public void visit(Integer element) {
System.out.println(element);
}
});
}
//Lambda简化
@Test
public void test03(){
int[] arr = new int[]{7,4,9,2,5,8,11,3};
BinarySearchTree<Integer> bst1 = new BinarySearchTree<>();
//将数据添加到BST中
Arrays.stream(arr).forEach(bst1::add);
bst1.leverOrderTraversal(System.out::println);
}
其他的遍历方法也是一样,我们最后来测试一下所有的遍历方法
@Test
public void test03(){
int[] arr = new int[]{7,4,9,2,5,8,11,3};
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
//将数据添加到BST中
Arrays.stream(arr).forEach(bst::add);
//将二叉树的树型结构打印出来
BinaryTrees.println(bst);
//前序
System.out.print("前序:");
bst.preorderTraversal(e -> System.out.print(e + " "));
System.out.println();
//中序
System.out.print("中序:");
bst.inorderTraversal(e -> System.out.print(e + " "));
System.out.println();
//后序
System.out.print("后序:");
bst.postorderTraversal(e -> System.out.print(e + " "));
System.out.println();
//层次遍历
System.out.print("层序:");
bst.leverOrderTraversal(e -> System.out.print(e + " "));
}
结果:
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
前序:7 4 2 3 5 9 8 11
中序:2 3 4 5 7 8 9 11
后序:3 2 5 4 8 11 9 7
层序:7 4 9 2 5 8 11 3
5.2 增强对外遍历暴露的接口
我们现在实现的遍历接口还有一个缺点,那就是当调用者调用遍历方法后就停不下来了,但是如果调用者遍历到每个数时就想要让这次遍历结束,我们的接口是不能实现的,所以我们还需要增强一下我们的接口
核心是将接口提供的回调函数的返回值改为布尔类型,当其返回true时,遍历停止,但是递归遍历中是不能用返回值进行判断的,因为每一次递归都是一个新的方法,无法保存标记的属性,所以可以在将接口改成抽象类并增加一个属性
修改接口:(抽象类不能使用Lambda表达式,需要使用匿名内部类)
/**
* 遍历接口
* @param
*
* visit 返回true表示停止遍历
返回false表示不停止,继续遍历
*/
public abstract static class Visitor<E>{
/**
* stop用来标记递归遍历中是否需要停止遍历
*/
boolean stop = false;
abstract boolean visit(E element);
}
修改层次遍历:
/**
* 层次遍历接口暴露
* @param visitor 逻辑接口
*/
public void leverOrderTraversal(Visitor<E> visitor){
if(visitor == null || root == null) throw new IllegalArgumentException("Visitor不能为空");
Queue<Node<E>> queue = new LinkedList<>();
//将根结点入队
queue.offer(root);
while (!queue.isEmpty()){
//出队
Node<E> node = queue.poll();
//回调,将处理遍历数据的业务交给调用者,如果返回true停止遍历
if(visitor.visit(node.element)) return;
if(node.left !=null) queue.offer(node.left);
if(node.right !=null) queue.offer(node.right);
}
}
测试:
@Test
public void test03(){
int[] arr = new int[]{7,4,9,2,5,8,11,3};
BinarySearchTree<Integer> bst = new Binar
//将数据添加到BST中
Arrays.stream(arr).forEach(bst::add);
//打印树型结构
BinaryTrees.println(bst);
//层次遍历
System.out.print("层序:");
bst.leverOrderTraversal(new BinarySearchTree.Visitor<Integer>() {
@Override
boolean visit(Integer element) {
System.out.print(element + " ");
return element == 2;;
}
});
}
结果:
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
层序:7 4 9 2
修改后序遍历:
/**
* 后序遍历
*/
public void postorderTraversal(Visitor<E> visitor) {
if(visitor == null) throw new IllegalArgumentException("visitor不能为空");
postorderTraversal(root,visitor);
}
public void postorderTraversal(Node<E> node,Visitor<E> visitor) {
//第一个visitor.stop让递归终止
if (node == null || visitor.stop) return;
postorderTraversal(node.left,visitor);
postorderTraversal(node.right,visitor);
//第二个visitor.stop让调用者的业务逻辑停止
if(visitor.stop) return;
visitor.stop = visitor.visit(node.element);
}
修改中序遍历:
/**
* 中序遍历(递归实现)
*/
public void inorderTraversal(Visitor<E> visitor) {
if(visitor == null) throw new IllegalArgumentException("visitor不能为空");
inorderTraversal(root,visitor);
}
private void inorderTraversal(Node<E> node,Visitor<E> visitor) {
if (node == null) return;
inorderTraversal(node.left,visitor);
//回调
if(visitor.stop) return;
visitor.stop = visitor.visit(node.element);
inorderTraversal(node.right,visitor);
}
修改前序遍历:
/**
* 前序遍历
*/
public void preorderTraversal(Visitor<E> visitor) {
if(visitor == null) throw new IllegalArgumentException("visitor不能为空");
preorderTraversal(root,visitor);
}
private void preorderTraversal(Node<E> node, Visitor<E> visitor) {
if(node == null || visitor.stop) return;
//回调
if(visitor.stop) return;
visitor.stop = visitor.visit(node.element);
preorderTraversal(node.left,visitor);
preorderTraversal(node.right,visitor);
}
6. 各种遍历的应用
-
前序遍历可以用来打印二叉树
-
BST中序遍历的元素是升序或者降序,可以用来处理有序集合
-
后序遍历适用于一些先子后父的操作
-
层序遍历可以用来计算二叉树的高度和用来判断当前树是否是完全二叉树
-
判断二叉树高度
/** * 非递归返回树的高度 * * @return 树的高度 */ public int heightByLevelOrder() { Queue<Node<E>> queue = new LinkedList<>(); //将根结点入队 queue.offer(root); //记录树的高度 int height = 0; //记录每一层的元素数量 int levelSize = 1; while (!queue.isEmpty()) { //出队 Node<E> node = queue.poll(); //当前层元素减少 levelSize--; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); //访问下一层 if (levelSize == 0) { levelSize = queue.size(); height++; } } return height; } -
判断是否为完全二叉树
//修改一下node private static class Node<E> { E element;//当前结点保存的元素 Node<E> left;//左结点 Node<E> right;//右结点 Node<E> parent;//父结点 public Node(E element, Node<E> parent) { this.element = element; this.parent = parent; } public boolean isLeaf(){ return left == null && right == null; } public boolean hasTwoChildren(){ return left != null && right != null; } } /** * 判断该树是否是一棵完全二叉树 * @return true是
false不是 */ public boolean isComplete(){ if(root == null) return false; Queue<Node<E>> queue = new LinkedList<>(); //将根结点入队 queue.offer(root); //标记上一次访问的结点是否度为一且子树为左子树 boolean flag = false; //遍历所有结点 Node<E> node; while (!queue.isEmpty()) { //出队 node = queue.poll(); //上一次访问的结点左子树存在右子树不存在那么这次访问的结点必须是叶子结点 if(flag && !node.isLeaf()) return false; if(node.left != null){ queue.offer(node.left); }else if(node.right != null){ return false; } if(node.right != null){ queue.offer(node.right); }else { flag = true; } } return true; }
-
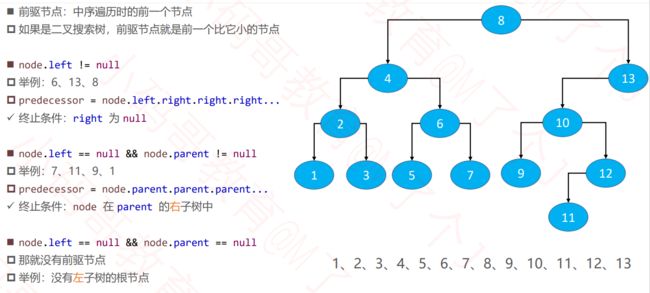
7. 前驱结点、后继结点
对于BST,某一个结点的前驱结点就是其
中序遍历的前一个元素
/**
* 找到当前结点的前驱结点
*/
public Node<E> predecessor(Node<E> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
//前驱结点在左子树当中(left.right.right.......)
Node<E> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
/*
* 这里有两种情况
* 1. node.parent == null
* 2. node = node.parent.right;
*/
return node.parent;
}
/**
* 找到其后继结点
*/
public Node<E> successor(Node<E> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
Node<E> p = node.right;
//第一种情况,其后继结点为node.right.left.left...
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
/*
* 来到这里有两种情况
* 1. node.right = null
* 2. node = node.parent.left;
*/
return node.parent;
}
8. remove方法实现
在二叉搜索树上删除结点的时候一定要注意需要维护好二叉搜索树的性质,也就是当前结点的左子树都比该结点小,右子树都比该结点大,其实形式上等价于中序遍历二叉搜索树的集合在删除某个数后再组成的二叉搜索树
删除结点一共已有三种情况:
- 删除的是叶子结点
- 删除的是度为1的结点
- 删除的是度为2的结点
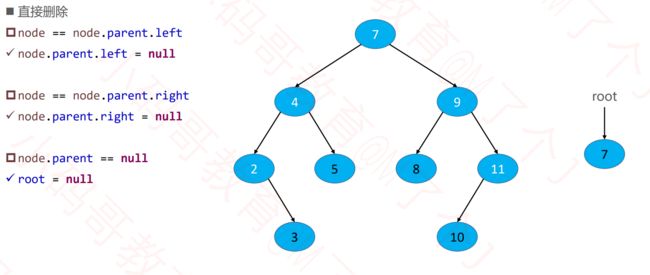
8.1 删除的是叶子结点
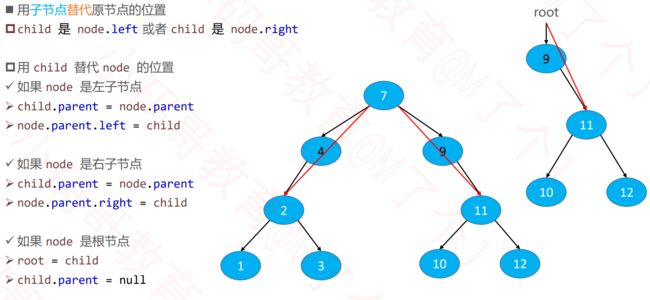
8.2 删除的是度为一的结点
8.3 删除的是度为二的结点
这里有两个结论需要重点记录一下:
- 度为一的结点其前驱或者后继结点的度为1或0
- 删除度为2的结点其实删除其前驱结点或者后继结点
第一点,为什么度为1的结点其前驱或者后继结点的度为1或0呢,我们回想一下BST的性质 ,在BST中当前结点的左子树都比其小,右子树都比其大,那么我们在找其前驱或者后继结点的时候按照第七点里面的步骤,有两种情况,第一种是node.left.right....或者node.right.left....,这样就一定会落到叶子结点上;第二种是node = node.parent.parent,这样的结点一定是度为1的结点
第二点,例如上面如果要删除7这个结点,那么做法是在左子树上找到其前驱结点4然后用7指向4的子节点,最后再用4覆盖7这个结点,这样就相当于是在找7的前驱结点并且删除它
8.4 代码实现
/**
* 对外暴露的删除方法
*/
public void remove(E element) {
remove(node(element));
}
/**
* 根据结点删除该结点
*/
private void remove(Node<E> node) {
if (node == null) return;
//优先处理度为2的结点
if (node.hasTwoChildren()) {
//找到其后继结点
Node<E> successor = successor(node);
//用后继结点的值覆盖度为2的结点的值
node.element = successor.element;
//因为度为2的结点的后继或者前驱结点一定是度为1或0,所以将删除结点交给后面的代码来做
node = successor;
}
//删除度为1或者度为0的结点
Node<E> replaceNode = node.left != null ? node.left : node.right;
/*
* 这里有三种情况,需要分类讨论
* 1. node是度为1的结点
* 2. node是叶子结点并且是根结点
* 3. node是叶子结点
*/
if (replaceNode != null) {
//先修改node.parent的指向
replaceNode.parent = node.parent;
//修改parent的left、right指向
if(node.parent == null){ //node是度为1的结点且是根结点
root = replaceNode;
}else if(node == node.parent.left){
node.parent.left = replaceNode;
}else {
node.parent.right = replaceNode;
}
} else if (node.parent == null) {
//node是叶子结点并且是根结点,直接让该结点为null
root = null;
} else {
//叶子结点
//父结点的左子树
if (node == node.parent.left) {
node.parent.left = null;
} else {
//父结点右子树
node.parent.right = null;
}
}
//将元素数量-1
size--;
}
/**
* 根据传入的元素找到结点
*/
private Node<E> node(E element) {
Node<E> node = root;
while (node != null) {
int cmp = compare(element, node.element);
if (cmp == 0) return node;
if (cmp > 0) {
node = node.right;
} else {
node = node.left;
}
}
//没找到
return null;
}
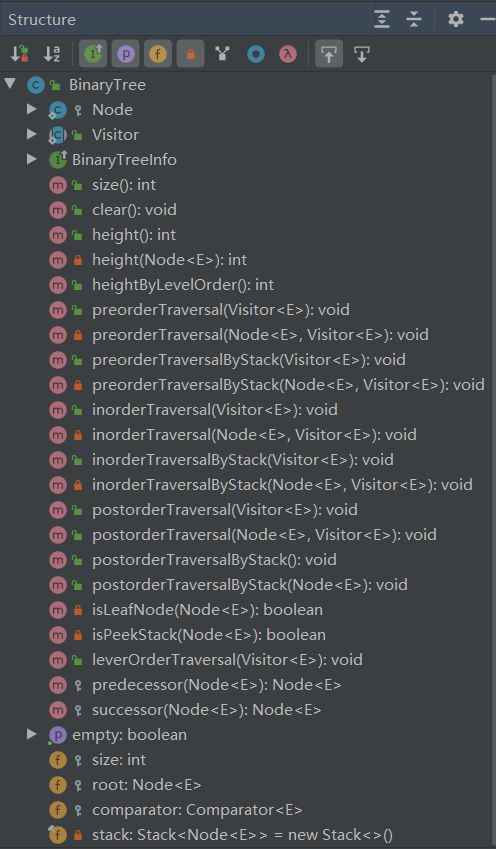
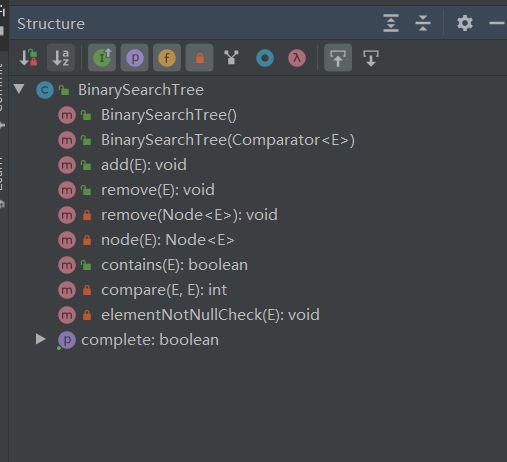
9. 设计继承结构,重构BST
我们需要将一些共有的方法提取出来,重新设计一下二叉搜索树与二叉树之间的继承结构
贴一下之间写的完整代码
package com.fx.binarySearchTree;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
/**
* @author: Eureka
* @date: 2022/3/14 20:12
* Description: 二叉搜索树
*/
@SuppressWarnings("unchecked")
public class BinarySearchTree<E> {
//结点以内部类的形式存在
private static class Node<E> {
E element;//当前结点保存的元素
Node<E> left;//左结点
Node<E> right;//右结点
Node<E> parent;//父结点
public Node(E element, Node<E> parent) {
this.element = element;
this.parent = parent;
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
}
private int size;//当前树结点个数
private Node<E> root;//根结点
private Comparator<E> comparator;//比较器
public BinarySearchTree() {
}
public BinarySearchTree(Comparator<E> comparator) {
this.comparator = comparator;
}
public void add(E element) {
//非空检测
elementNotNullCheck(element);
//先判断是否为根结点
if (root == null) {
root = new Node<>(element, null);
}
//非根结点,非递归进行添加
Node<E> node = root;//用来标记移动的结点
Node<E> parent = root;//保存当前结点的父结点,默认根结点就是父结点
//根据比较规则找到待添加元素的位置
int cmp = 0;
while (node != null) {
//比较值
cmp = compare(element, node.element);
//保存当前结点的父结点
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else {
return;
}
}
//添加元素
Node<E> newNode = new Node<>(element, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
}
/**
* 对外暴露的删除方法
*/
public void remove(E element) {
remove(node(element));
}
/**
* 根据结点删除该结点
*/
private void remove(Node<E> node) {
if (node == null) return;
//优先处理度为2的结点
if (node.hasTwoChildren()) {
//找到其后继结点
Node<E> successor = successor(node);
//用后继结点的值覆盖度为2的结点的值
node.element = successor.element;
//因为度为2的结点的后继或者前驱结点一定是度为1或0,所以将删除结点交给后面的代码来做
node = successor;
}
//删除度为1或者度为0的结点
Node<E> replaceNode = node.left != null ? node.left : node.right;
/*
* 这里有三种情况,需要分类讨论
* 1. node是度为1的结点
* 2. node是叶子结点并且是根结点
* 3. node是叶子结点
*/
if (replaceNode != null) {
//先修改node.parent的指向
replaceNode.parent = node.parent;
//修改parent的left、right指向
if(node.parent == null){ //node是度为1的结点且是根结点
root = replaceNode;
}else if(node == node.parent.left){
node.parent.left = replaceNode;
}else {
node.parent.right = replaceNode;
}
} else if (node.parent == null) {
//node是叶子结点并且是根结点,直接让该结点为null
root = null;
} else {
//叶子结点
//父结点的左子树
if (node == node.parent.left) {
node.parent.left = null;
} else {
//父结点右子树
node.parent.right = null;
}
}
}
/**
* 根据传入的元素找到结点
*/
private Node<E> node(E element) {
Node<E> node = root;
while (node != null) {
int cmp = compare(element, node.element);
if (cmp == 0) return node;
if (cmp > 0) {
node = node.right;
} else {
node = node.left;
}
}
//没找到
return null;
}
public boolean contains(E e) {
return node(e) != null;
}
/**
* 规定传入对象的比较规则
*
* @param e1 第一个对象
* @param e2 第二个对象
* @return 0表示相等,大于0表示 e1 > e2,小于0表示 e2 < e1
*/
private int compare(E e1, E e2) {
if (comparator != null) {
return comparator.compare(e1, e2);
}
return ((java.lang.Comparable<E>) e1).compareTo(e2);
}
/**
* 返回树结点个数
*/
public int size() {
return size;
}
/**
* 判断树是否为空
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 清空当前树
*/
public void clear() {
root = null;
size = 0;
}
/**
* 判断元素是否为空
*/
private void elementNotNullCheck(E element) {
if (element == null) {
throw new IllegalArgumentException("element must not be null");
}
}
/**
* 递归输出树的高度
*
* @return 返回树的高度
*/
public int height() {
return height(root);
}
private int height(Node<E> node) {
if (node == null) return 0;
return 1 + Math.max(height(node.left), height(node.right));
}
/**
* 非递归返回树的高度
*
* @return 树的高度
*/
public int heightByLevelOrder() {
Queue<Node<E>> queue = new LinkedList<>();
//将根结点入队
queue.offer(root);
//记录树的高度
int height = 0;
//记录每一层的元素数量
int levelSize = 1;
while (!queue.isEmpty()) {
//出队
Node<E> node = queue.poll();
//当前层元素减少
levelSize--;
if (node.left != null) queue.offer(node.left);
if (node.right != null) queue.offer(node.right);
//访问下一层
if (levelSize == 0) {
levelSize = queue.size();
height++;
}
}
return height;
}
/**
* 判断该树是否是一棵完全二叉树
*
* @return true是
false不是
*/
public boolean isComplete() {
if (root == null) return false;
Queue<Node<E>> queue = new LinkedList<>();
//将根结点入队
queue.offer(root);
//标记上一次访问的结点是否度为一且子树为左子树
boolean flag = false;
//遍历所有结点
Node<E> node;
while (!queue.isEmpty()) {
//出队
node = queue.poll();
//上一次访问的结点左子树存在右子树不存在那么这次访问的结点必须是叶子结点
if (flag && !node.isLeaf()) return false;
if (node.left != null) {
queue.offer(node.left);
} else if (node.right != null) {
return false;
}
if (node.right != null) {
queue.offer(node.right);
} else {
flag = true;
}
}
return true;
}
/**
* 遍历接口
*
* @param visit 返回true表示停止遍历
返回false表示不停止,继续遍历
*/
public abstract static class Visitor<E> {
/**
* stop用来标记递归遍历中是否需要停止遍历
*/
boolean stop = false;
abstract boolean visit(E element);
}
/**
* 前序遍历
*/
public void preorderTraversal(Visitor<E> visitor) {
if (visitor == null) throw new IllegalArgumentException("visitor不能为空");
preorderTraversal(root, visitor);
}
private void preorderTraversal(Node<E> node, Visitor<E> visitor) {
if (node == null) return;
//回调
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
preorderTraversal(node.left, visitor);
preorderTraversal(node.right, visitor);
}
/**
* 栈实现前序遍历
*/
private final Stack<Node<E>> stack = new Stack<>();
public void preorderTraversalByStack(Visitor<E> visitor) {
if (root == null) throw new IllegalArgumentException("Visitor不能为空");
//将根元素入栈
preorderTraversalByStack(root, visitor);
}
private void preorderTraversalByStack(Node<E> popNode, Visitor<E> visitor) {
while (popNode != null) {
//回调
if (visitor.stop) return;
visitor.stop = visitor.visit(popNode.element);
//将其右结点入栈
if (popNode.right != null) {
stack.push(popNode.right);
}
//将其左结点入栈
if (popNode.left != null) {
stack.push(popNode.left);
}
//将栈顶元素出栈
popNode = stack.isEmpty() ? null : stack.pop();
}
}
/**
* 中序遍历(递归实现)
*/
public void inorderTraversal(Visitor<E> visitor) {
if (visitor == null) throw new IllegalArgumentException("visitor不能为空");
inorderTraversal(root, visitor);
}
private void inorderTraversal(Node<E> node, Visitor<E> visitor) {
if (node == null || visitor.stop) return;
inorderTraversal(node.left, visitor);
//回调
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
inorderTraversal(node.right, visitor);
}
/**
* 中序栈实现
*/
public void inorderTraversalByStack(Visitor<E> visitor) {
if (root == null || visitor == null) throw new IllegalArgumentException("Visitor不能为空");
inorderTraversalByStack(root, visitor);
}
private void inorderTraversalByStack(Node<E> popNode, Visitor<E> visitor) {
//只要左结点存在就一直入栈
while (true) {
if (popNode != null) {
stack.push(popNode);
popNode = popNode.left;
} else {
if (stack.isEmpty()) return;
popNode = stack.pop();
//回调
visitor.visit(popNode.element);
popNode = popNode.right;
}
}
}
/**
* 后序遍历
*/
public void postorderTraversal(Visitor<E> visitor) {
if (visitor == null) throw new IllegalArgumentException("visitor不能为空");
postorderTraversal(root, visitor);
}
public void postorderTraversal(Node<E> node, Visitor<E> visitor) {
if (node == null || visitor.stop) return;
postorderTraversal(node.left, visitor);
postorderTraversal(node.right, visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
}
/**
* 后序遍历非递归实现
*/
public void postorderTraversalByStack() {
postorderTraversalByStack(root);
}
public void postorderTraversalByStack(Node<E> root) {
if (root == null) return;
Stack<Node<E>> stack = new Stack<>();
stack.push(root);
Node<E> temp = null;
while (!stack.isEmpty()) {
temp = stack.pop();
//业务逻辑
System.out.println(temp);
if (temp.left != null) {
stack.push(temp.left);
}
if (temp.right != null) {
stack.push(temp.right);
}
}
}
private boolean isLeafNode(Node<E> node) {
System.out.println(node.element);
return node.left == null && node.right == null;
}
private boolean isPeekStack(Node<E> node) {
return stack.peek().left == node || stack.peek().right == node;
}
/**
* 层序遍历接口暴露
*
* @param visitor 逻辑接口
*/
public void leverOrderTraversal(Visitor<E> visitor) {
if (visitor == null || root == null) throw new IllegalArgumentException("Visitor不能为空");
Queue<Node<E>> queue = new LinkedList<>();
//将根结点入队
queue.offer(root);
while (!queue.isEmpty()) {
//出队
Node<E> node = queue.poll();
//回调,将处理遍历数据的业务交给调用者
if (visitor.visit(node.element)) return;
if (node.left != null) queue.offer(node.left);
if (node.right != null) queue.offer(node.right);
}
}
/**
* 找到当前结点的前驱结点
*/
public Node<E> predecessor(Node<E> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
//前驱结点在左子树当中(left.right.right.......)
Node<E> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
/*
* 这里有两种情况
* 1. node.parent == null
* 2. node = node.parent.right;
*/
return node.parent;
}
/**
* 找到其后继结点
*/
public Node<E> successor(Node<E> node) {
if (node == null) throw new IllegalArgumentException("node不能为空");
Node<E> p = node.right;
//第一种情况,其后继结点为node.right.left.left...
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
//从祖父结点里面找
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
/*
* 来到这里有两种情况
* 1. node.right = null
* 2. node = node.parent.left;
*/
return node.parent;
}
}
现在我们需要把二叉树共有的方法提取出来,我这里放一张共有方法的图
BinaryTree
BST
这里要注意的是用于继承的方法要将访问权限修改为protected,然后一棵BST就写好了