Pytorch-1.3 认识tensor【1】storage()和storage.offset()、shape和size()、stride()、t()和transpose()

前言 tensor简介
张量是指将向量和矩阵推广到任意维数的一种数据结构，它存储使用索引可以单独访问的数字集合，并且可以使用多个索引进行索引。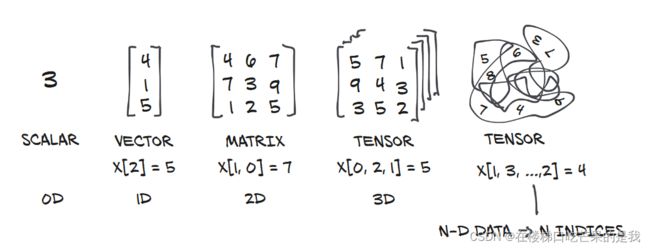
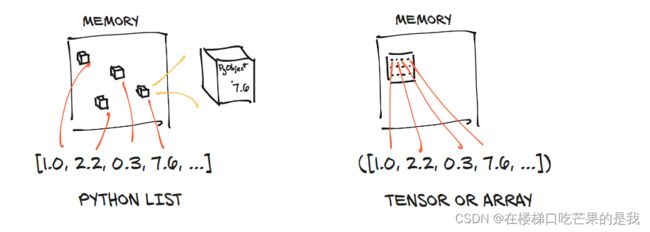
Python中的列表或数字元组是在内存中单独分配的Python对象的集合；而PyTorch张量或NumPy数组是分配在连续的内存块中。如图：

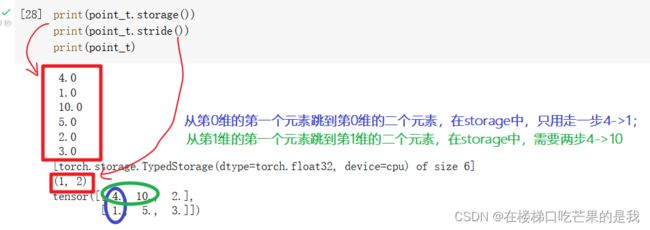
1.storage()和storage.offset()

通过storage()和storage.offset()来理解tensor的内存

storage()返回的是内存的存储信息。
storage.offset()返回tensor的第一个元素与storage的第一个元素的偏移量。

pytorch中的一个tensor分为头信息区（Tensor）和存储区（Storage），信息区主要保存着tensor的形状（size）、步长（stride）、数据类型（type）等信息。
  而真正的数据则保存成连续数组，存储在存储区。一般一个tensor都会有相对应的Storage，但也有另一种情况时多个tensor都对应着相同的一个Storage，这几个tensor只是头信息区不同。

实际操作再来理解一下：

import torch
#创建一个2维张量
points_3 = torch.tensor([[4.,1.],[2.,5.],[2.,3.]])
points_3
>>> tensor([[4., 1.],
        [2., 5.],
        [2., 3.]])

#查看points_3的存储内容
points_3.storage()
>>> 4.0
 1.0
 2.0
 5.0
 2.0
 3.0
[torch.storage.TypedStorage(dtype=torch.float32, device=cpu) of size 6]

再创建一个张量，让我们理解一下“另一种情况时，多个tensor都对应着相同的一个Storage，这几个tensor只是头信息区不同”这句话。

#再创建一个张量second_points_3
#second_points_3为points_3的第一行
second_points_3 = points_3[1]
second_points_3
>>>tensor([2., 5.])

已知storage.offset()的作用是返回tensor的第一个元素与storage的第一个元素的偏移量，我们可以查看一下second_points_3.storage.offset()：

#返回second_points_3在原张量（points_3）中起点的索引号
second_points_3.storage_offset()
>>>2

返回索引 [2] 即points_3.storage()中的第三个位置，这就说明second_points_3并不是重新开了一个内存再赋值；而是指向了points_3中的部分存储。也就是说多个张量确实可以索引相同的存储，即使它们对数据的索引方式不同。
再进一步验证一下，我们可以尝试：通过second_points_3是否可以更改points_3对应内存的中值，来验证他们是不是真的对应同一段内存。

#验证一下second_points_3是否与points_3共用内存
#令second_points_3的第一个值改为10，原数值为2.
second_points_3[0]=10
second_points_3,points_3
>>>(tensor([10.,  5.]), tensor([[ 4.,  1.],
         [10.,  5.],
         [ 2.,  3.]]))

可以看到，修改一个张量元素的值，另一个张量元素的值也同时改变，这进一步说明了：second_points_3确实与points_3共用内存。

所以之后如果我们需要使新张量的值等同于另一个张量的部分，那我们应该这样做：

anther_points = points_3[1].clone()
anther_points,anther_points.storage_offset()
>>>(tensor([10.,  5.]), 0)

再用同样的方法验证：

anther_points[0]=20
points_3,anther_points
>>>(tensor([[ 4.,  1.],
         [10.,  5.],
         [ 2.,  3.]]), tensor([20.,  5.]))

2.shape和size()

shape和size()两者作用类似，前者是一个函数，后者是一个属性。

points_3.size(),points_3.shape
>>>(torch.Size([3, 2]), torch.Size([3, 2]))

3.stride()

stride是在指定维度dim中从一个元素跳到下一个元素所必需的步长。当没有参数传入时，返回所有步长的元组。否则，将返回一个整数值作为特定维度dim中的步长。

points_3,points_3.stride()
>>>(tensor([[ 4.,  1.],
         [10.,  5.],
         [ 2.,  3.]]), (2, 1))

points_3是一个二维三行两列的张量，stride()返回的结果（2，1）意思是，从第0个维度中第一个元素【4.】跳到第二个元素【10.】需要两步；从第1个维度中第一个元素【4.】跳到第二个元素【1.】需要一步。
更直观地，我们可以设置dim的值查询对应维度，从一个元素跳到第二个元素要几步：

#返回一个整数值作为特定维度dim中的步长。
points_3.stride(0)
>>>2
points_3.stride(1)
>>>1

再来看一下一维张量second_points_3，因为是一维的，所以从一个元素到另一个元素只需要一步。

second_points_3,second_points_3.stride()
>>>(tensor([10.,  5.]), (1,))

4.t()和transpose(）

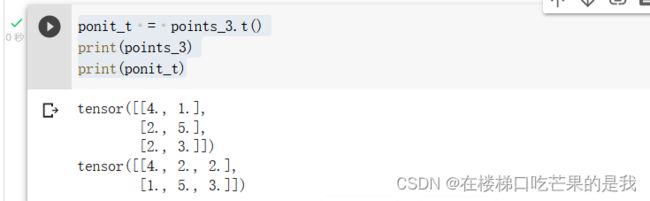
ponit_t = points_3.t()
print(points_3)
print(ponit_t)

一件重要的事：
转置并不会开辟新的内存，仍然使用的是points_3指向的内存。

id(points_3.storage()) == id(ponit_t.storage())
>>>True

用这张图再来理解一下stride()的意思。

三维张量以上就不能使用转置了，可以用transpose来交换矩阵的两个维度：

#创建一个三维的张量，可以猜一下它的stride()输出
some_t = torch.ones(3,4,5)
some_t.stride()
>>>(20, 5, 1)

也就是说，从第0维的第一个元素到第0维的第二个元素需要跳4*5=20步；从第1维的第一个元素到第1维的第二个元素需要跳5步；从第2维的第一个元素到第2维的第二个元素需要跳1步。
此时我们运行用transpose()将第0维和第2维交换。

#transpose同样没有新建内存
transpose_t = some_t.transpose(0,2)
transpose_t.shape
>>>torch.Size([5, 4, 3])

那么它的stride()输出会是怎么样的，大胆猜测一下：

transpose_t.stride()
>>>(1, 5, 20)

为什么会变化，主要是因为transpose（）也是指向原来的内存，只是索引顺序发生了改变，可以看到使用is_contiguous()函数来判断内存是否连续，变换前的张量some_t指向的内存就是连续的，而转换后的就是不连续的了，这就导致stride()不同维度的跳跃步长发生了变化。

#is_contiguous()判断内存是否连续
print(some_t.is_contiguous())
print(transpose_t.is_contiguous())
>>>True
>>>False

参考：
1.pytorch笔记（一）——tensor的storage()、stride()、storage_offset（）