【Java集合 从源码透析,月薪上万不是梦】简单理解
集合源码解析
-
-
- 一、前言
- 二、List集合
-
- (一) ArrayList
-
- (1)ArrayList的方法
- (2)ArrayList底层源码实现和解析
- (二) LinkdedList
-
- (1)LinkdedList的方法
- (2)LinkdedList底层源码实现和解析
- (三)Arraylist和Linkedlist异同
- (四)使用 LinkedList,而不用ArrayList场景
- (五)Vector和Arraylist异同
- 二、HashMap集合
-
- (一)Hashmap不足
- (二)LinkedHashmap
- (三)TreeMap
-
一、前言
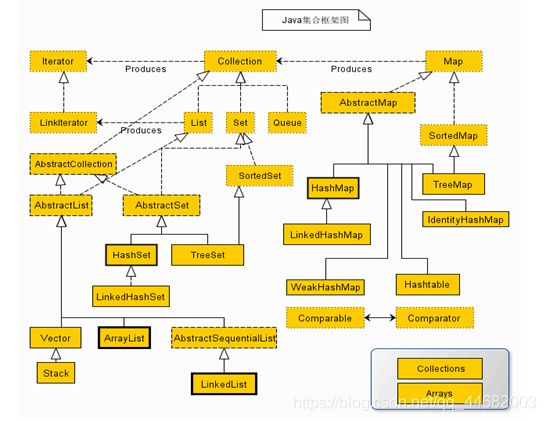
- 上图是java集合框架图,我们可以看到java集合类主要由三个接口派生而出,即Collection和Map接口和Iterator
- java有三种集合,包括Set、List和Map,它们都处于java.util包中,Set、List和Map都是接口,它们有各自的实现类。
- Iterator,所有的集合类,都实现了Iterator接口,这是一个用于遍历集合中元素的接口,主要包含以下三种方式:
1、hasNext()判断是否还有下一个元素。
2、next()放回下一个元素。
3、remove()删除当前元素。
每个接口都有自己的特性,下面来一一分析
二、List集合
- List集合特点:list集合代表一个元素是有序的且可以重复的集合,集合中每个元素都有其对应的顺序索引;list集合允许添加重复数据,可以通过索引方式来访问指定位置的元素
- List接口的两个常用实现类:ArrayList和LinkedList
(一) ArrayList
- ArrayList:底层是数组,长度可变;其实就是对数组进行封装,元素满后自动扩容
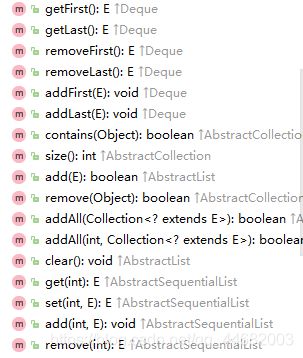
(1)ArrayList的方法
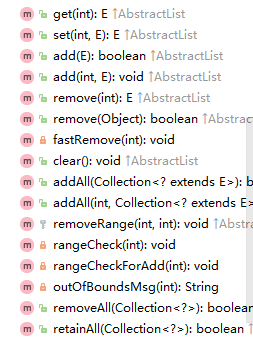
我们在使用这些方法都是直接用,但面试官可不允许这样,面试官更看中的是底层源码实现和理解,下面我用代码来实现下:ArrayList底层源码
(2)ArrayList底层源码实现和解析
下面是我手写的模拟ArrayList底层源码实现的
public class MyArrayList{
private Object[]element;
private static final int DEFAULT_CAPACITY = 10;
private static final Object[] EMPTY_ELEMNRT = {};
private int size ;//有效个数
private class Itr implements Iterator{
private int cur;//当前元素下标
int lastcur = -1;//返回下标
@Override
public boolean hasNext() {//判断遍历是否结束
return cur!=size;
}
@Override
public T next() {//取到当前元素的方法next(),并且移动到下一元素位置
int newcur = cur;//保存当前的cur下标
if (newcur>=size){
throw new NoSuchElementException();
}
cur = newcur + 1;
return (T)element[lastcur = newcur];
}
@Override
public void remove() {
if (lastcur<0){
throw new Error ("元素为空");
}
MyArrayList.this.remove(lastcur);
cur = lastcur;
lastcur = -1;
}
}
//返回这个类
public Iterator iterator() {
return new Itr();
}
public MyArrayList() {
element = EMPTY_ELEMNRT;
}
//返回数组元素个数
public int size() {
return size;
}
//判断下标
public void rangeCheck(int index) {
if (index >= size || index < 0) {
throw new IndexOutOfBoundsException();
}
}
//扩容
public void ensureCapacity(int size) {
if (size > element.length){
grow(size);
}
}
private void grow(int size) {
if (size == 1){
element = new Object[DEFAULT_CAPACITY];
return;
}
int oldsize = element.length;
int newsize = oldsize+(oldsize>>1);
element = Arrays.copyOf(element,newsize);
}
//增加元素
public void add(T value) {
ensureCapacity(size+1);
element[size++] = value;
}
//指定下标插入元素
public void add(int index, T value) {
rangeCheck(index);
ensureCapacity(size+1);
System.arraycopy(element, index, element, index + 1, size - index);
element[index] = value;
size++;
}
//删除指定下标元素
public void remove(int index) {
rangeCheck(index);
System.arraycopy(element,index+1,element,index,size-index-1);
element[size-1] =null;
size--;
}
//返回指定下标元素
public T getIndex(int index) {
rangeCheck(index);
return (T)element[index];
}
//修改指定下标元素
public void setIndex(int index,T value) {
rangeCheck(index);
element[index] = value;
}
public void show(){
for (int i = 0;i 对上述部分代码进行解析
- 1
private static final Object[] EMPTY_ELEMNRT = {};
public MyArrayList() {
element = EMPTY_ELEMNRT;
}
我们可以看到我们在调用MyArraylist时候,element给我们是空的数组,这样做有什么好处?
回答:也就是在调用MyArraylist时候,并不会直接给我们开辟内存,避免了内存的浪费,那什么时候开辟呢?看底下
- 2
//指定下标插入元素
public void add(int index, T value) {
rangeCheck(index);
ensureCapacity(size+1);
System.arraycopy(element, index, element, index + 1, size - index);
element[index] = value;
size++;
}
//判断下标
public void rangeCheck(int index) {
if (index >= size || index < 0) {
throw new IndexOutOfBoundsException();
}
}
//扩容
public void ensureCapacity(int size) {
if (size > element.length){
grow(size);
}
}
private void grow(int size) {
if (size == 1){
element = new Object[DEFAULT_CAPACITY];
return;
}
int oldsize = element.length;
int newsize = oldsize+(oldsize>>1);
element = Arrays.copyOf(element,newsize);
}
我们看到增加元素时候:add(int index, T value),会先 判断断下标:rangeCheck(index);是否扩容:ensureCapacity(size+1);
例如:现在空集合,size=0;增加第一个元素,通过rangeCheck(index)后,进入到ensureCapacity(size+1),进入grow(size),判断size == 1;然后这时候才分配内存;同时扩容操作也是在 grow(size)中完成的。
(二) LinkdedList
-
LinkdedList:底层用双向链表实现的存储。特点:查询效率低,增删效率高,线程不安全。
-
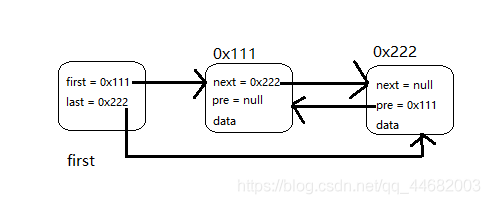
双向链表也叫双链表,是链表的一种,它的每个数据节点中都有两个指针,分别指向前一个节点和后一个节点。 所以,从双向链表中的任意一个节点开始,都可以很方便地找到所有节点。LinkedList储存结构图如下:
-
双向链表有一个头结点:first,没有data数字域,first其实就是一个标记,first保存的下一节点内存地址;last保存的是链表最后一个节点的内存地址
-
节点:我们看到每个节点有三部分,当然data就是存储的元素,next保存的是下一节点的内存地址;pre保存的是上一节点的内存地址
(1)LinkdedList的方法
- LinkdedList特有的方法:
- 1:添加
addFirst (开头添加)
addLast(末尾添加)
- 2:获取
getFirst()
getLast()
3:删除
removefirst()
removeLast()
下面我模拟LinkdedList源码来实现LinkdedList部分方法
(2)LinkdedList底层源码实现和解析
- 1、LinkdedList结构实现
public class MyLinkedlist {
private Node first;//头指针
private Node last;//指向末尾节点,形成双链表
private int size ;//有效个数
//节点
private static class Node{
Node pre;//指向上一节点
Node next;//指向下一节点
E element;//数据域
//构造方法
public Node(Node pre, Node next, E element) {
this.pre = pre;
this.next = next;
this.element = element;
}
}
- 2、LinkdedList公用的方法
(2.1)返回查找index后的节点
public Node node(int index) {
Node x = first;
//优化
//先判断index靠近头,还是靠近尾,再决定从哪里找(实现:index和size/2比较)
if (index > (size >> 1)) {
//靠近尾
x = last;
for (int i = size-1; i>index; i--) {
x = x.pre;
}
} else {//靠近头
for (int i = 0; i < index; i++) {
x = x.next;
}
}
return x;
}
说明: 通过对index和size/2的比较,可以判断查找index靠近头还是尾,遍历节约时间
(2.2)判断index>=0 && index
//判断索引是否合法
private void checkElementIndex(int index){
if (!isElementIndex(index)){
throw new IndexOutOfBoundsException("Index:"+ index+ "Size:"+ size);
}
}
//判断索引是否满足条件
private boolean isElementIndex(int index) {
return index>=0 && index(2.3)判断index>=0 && index <=size
private void checkPostionIndex(int index){
if (!isPostionIndex(index)){
throw new IndexOutOfBoundsException("Index:"+ index+ "Size:"+ size);
}
}
private boolean isPostionIndex(int index) {
return index>=0 && index<=size;
}
- 3、LinkdedList的get方法
// 说明:我们找index下标元素,需要从first节点出发找index次 first->1->2->3
public T get(int index){
checkElementIndex(index);
return node(index).element;//返回节点的元素
}
说明: 我们要找index下标元素,然后对下标index判断,通过node(int index)返回对应的节点
- 4、LinkdedList的add方法
// 注意:这里index 可以等于size,也就是最后添加元素
public void add(int index, T element) {
checkPostionIndex(index);
if (index == size){//头添加/尾添加
linklast(element);
}else {
linkBefore(element,node(index));
}
size++;
}
private void linklast(T element) {
//思路:拿到last节点 构建node完成指向关系 修改last指向
Node x = last;
Node newnode = new Node(x,null,element);
last = newnode;
if (x==null){
first = newnode;
} else {
x.next = newnode;
}
}
private void linkBefore(T element,Node node){
Node pre = node.pre;//前一个节点
Node newnode = new Node<>(pre,node,element);//新节点信息,这时候只是建立新节点pre和next单线
node.pre = newnode;//下一节点pre指向新节点
注意:index为0时 pre为空,空指针异常
if (pre==null){
first = newnode;
}else {
pre.next = newnode;//上一节点next指向新节点
}
}
注意: index == size有两种特殊情况,一种index = size !=0,也就是尾插;另一种情况index = size = 0,也就是链表为空插入;
当index!=size时候,也有两种情况,一种是头插入(即:pre为空,它就是frist指向的节点),一种是中间插入(即:pre和next都不为空)
- 5、LinkdedList的remove方法
public T remove(int index){
checkElementIndex(index);
modCount++;
Node node = node(index);
Node pre = node.pre;//前一节点
Node next = node.next;//后一节点
//分析 删除节点为头节点/尾节点 空指针异常
if (pre ==null){
first = next;
next.pre = null;
}else {
pre.next = next;
}
if (next == null){
last = pre;//注意:这里只写:last = pre一条语句可以完成删除操作,但node.pre这个引用
//并未断掉,还是指向pre的,根据垃圾回收,它是可以到达:可达性分析oot节点的,不会被回收
//所以,我们要添加底下一行代码:node.pre = null; 断掉node的所有指向引用
node.pre = null;
}else {
next.pre = pre;
}
size--;
return node.element;
}
注意: 源码对remove实现是这样的,正常的我们中间删除一个节点node,那就让node的前一节点的next指向node下一节点,node的下一节点的pre指向node前一节点,但这样有问题:node的前一节点和下一节点都可能为空,此时会有空指针异常;源码对这两种情况分类讨论,也就是我上面对pre和next的讨论
(三)Arraylist和Linkedlist异同
- ArrayList是基于索引的数据接口,它的底层是数组。它可以以O(1)时间复杂度对元素进行随机访问。与此对应,LinkedList是以元素列表的形式存储它的数据,每一个元素都和它的前一个和后一个元素链接在一起,在这种情况下,查找某个元素的时间复杂度是O(n)。
- 相对于ArrayList,LinkedList的插入,添加,删除操作速度更快,因为当元素被添加到集合任意位置的时候,不需要像数组那样重新计算大小或者是更新索引。
- LinkedList比ArrayList更占内存,因为LinkedList为每一个节点存储了两个引用,一个指向前一个元素,一个指向下一个元素。
(四)使用 LinkedList,而不用ArrayList场景
- 你的应用不会随机访问数据 。因为如果你需要LinkedList中的第n个元素的时候,你需要从第一个元素顺序数到第n个数据,然后读取数据。
- 你的应用更多的插入和删除元素,更少的读取数据 。因为插入和删除元素不涉及重排数据,所以它要比ArrayList要快。
换句话说,ArrayList的实现用的是数组,LinkedList是基于链表,ArrayList适合查找,LinkedList适合增删
(五)Vector和Arraylist异同
- 使用上: 两者方法实现几乎都是一样的
- 源码
1、底层数据结构:完全相同
2、构造函数
Arraylist初始数组大小为空,在添加第一个元素时候,数组容量大小为:10
Vector初始数组大小就为:10
3、grow函数比较
Arraylist:当添加第一个元素,判断size = 1,开辟10个格子大小,然后后面就是:1.5倍扩容
Vector:Vector存在一个增长因子:capacityIncrement,扩容时候会先判断capacityIncrement,若capacityIncrement不大于0,Vector默认2倍扩容,否则扩大capacityIncrement个大小
分析: 增长因子的存在有什么好处,对于Arraylist来说,对于数据越多时候,1.5倍扩容内存也是很大的,但我们数据如果远远小于扩容的大小,会造成很大的浪费;而 增长因子:capacityIncrement存在很好的解决了这个问题,但capacityIncrement也有弊端,设置太小,而数据太多,会造成频繁的扩容,所以要结合实际情况
4、Vector线程安全
Vector所有方法都添加了:synchronized锁,所以Vector是线程安全的集合,而Arraylist没有加锁处理,所以Arraylist线程不安全
二、HashMap集合
一、存储方式:
JDK1.8之前是:**数组+链表**存储结构
JDK1.8之后是:**数组+链表+红黑树**存储结构
二、存储特点:
1、存储无序
2、键值对都可以为null,但键位置只能是一个null
3、阈值>8并且数组长度大于64,才可以将链表转换成红黑树,目的是为了高效的查询
三、面试及重点知识
1、哈希底层采用何种算法计算hash值?还有哪些算法可以算出hash值?
答:底层采用的key的hashCode方法的值结合数组长度进行无符号右移(>>>),按位异或(^),按位与(&)计算出索引;还可以采用平方取中法,取余数,伪随机数法
2、当两个对象hashCode一样会怎么样
答:会发生哈希碰撞,若key值一样就会替换旧的Value,否则连接到链表后(JDK1.8后采用的尾插,之前是头插法)。链表长度超过阈值8就转换成红黑树结构存储
3、何时发生哈希碰撞,如何解决
答:当两个元素的Key值计算出的hashCode相同,也就是对应同一个数组下标就会发生哈希碰撞。jdk1.8之前采用的链表,jdk1.8后采用的链表+红黑树解决问题的
4、若两个键的hashCode相同,如何存储键值对
相同时,通过equls比较内容是否相同,相同则替换旧的value,否则添加新的键值对
5、为什么jdk1.8引入红黑树
答:哈希函数固然很巧妙,但也不可能达到元素百分百的均匀分布。当元素很多时候,不可避免的会发生哈希碰撞,这会导致链表长度很长,我们知道单链表的遍历时间复杂度:O(n),数据越多,hashCode优势越小,向单链表靠近。为此,引入红黑树(查找时间复杂度logn)来优化这个问题。
6、为什么Map链表节点个数超过8才可以转成红黑树
因为树的节点的大小约是普通节点的两倍,所以我们只在箱子包含足够的节点时才使用树结构。当它们变得太少(降到6 由于删除调整),就会又变回去(链表)。理想情况下:在随机哈希码下,链表中节点的频率服从泊松分布:
第一个值是:
0: 0.605
1: 0.3032
…
8: 0.00000006
8时候,概率非常小了
四、集合类的成员
一、集合的初始化容量(必须是2的n次幂)
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
问题:为什么必须是2的n次幂?不是2的n次幂会怎么样?
答:首先,为了减少哈希冲突,我们采用算法:hash%length取模来完成,但计算机中直接求余效率不如位运算,源码采用的是:hash&(length-1)
来运算,上述两式相等的前提就是:length是2的n次幂
再问:为什么这样就可以减少哈希碰撞呢?
答:2的n次方实际就是1后面个0;2的n次方-1,就是n个1,按位运算:二进制上,同1则1,否则为0.
举例:3&(8-1)还是3;2&(8-1)还是2,计算出的索引不同
二、传参时候,初始容量不是2的n次幂会如何
源码:
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
此方法会找到大于等于传参的最小的2的n次幂
怎么实现的呢,我们来分析下:

其实经过上述测试,我们看到最终的,我们得到:00001111,后几位是连续的1
注意:容量最大也就是32bit的正数,因此最后n|=n>>>16,最多也就32个1(但有符号位存在,这时候是负数,所以在执行tableSizeFor前,先对initialCapacity判断,如果大于
MAXIMUM_CAPACITY(2^30),则取MAXIMUM_CAPACITY。如果等于,会进行移位操作。所以这里移位操作最大30个1,不会大于等于MAXIMUM_CAPACITY。30个1,加上1之后是
2^30 )
三、加载因子和负载因子
int threshold;//负载因子
static final float DEFAULT_LOAD_FACTOR = 0.75f;//加载因子
负载因子:当实际大小(容量*负载因子)超过临界值,会进行扩容
加载因子:用来衡量hashmap满的程度,表示hashmap疏密程度,计算加载因此方法 = size/capacity(12/16).。加载因子太大导致查找元素效率低,因为越大也就意味着你的扩容时机越晚,会存储更多的元素。
四、扩容方法resize
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];//32
transfer(newTable, initHashSeedAsNeeded(newCapacity));
table = newTable;
threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}
1、什么时候扩容
当hashmap中元素个数大于数组长度*加载因子时候们就会扩容,就会把数组扩大一倍,然后重新计算各个元素在数组中的位置,而这是一个非常耗性能的操作,所以最好,我们可以知道我们需要多少元素,节省性能
补充:
当hashmap中其中一个链表的对象达到8时,此时数组长度没有达到64,那么hashmap会先用扩容解决,如果已经达到了64,那么这个链表才会被转换成红黑树,节点类型也会给改变。
2、扩容是什么
hashmap中进行扩容,使用的rehash非常巧妙
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length;
for (Entry e : table) {
while(null != e) {
Entry next = e.next;
if (rehash) {
e.hash = null == e.key ? 0 : hash(e.key);
}
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];//x
newTable[i] = e;
e = next;
}
}
}
因为每次每次扩容都是翻倍,与原来计算的(n-1)&hash的结果相比,只是多了一个bit位,所以节点要么在原来位置,要么被分配到“原位置+旧容量”
(一)Hashmap不足
一、浪费空间
开始我们存储元素,会开辟16个桶子大小,当加载因子是0.75,可以存储size = 12个元素
哈希冲突最大时候:所有元素对应一个下标
哈希冲突最小:每个元素都占一个下标
空间利用率高,元素数量多,哈希冲突高,查询效率低
二、依赖哈希算法
哈希算法设计的好,查询效率高
哈希算法设计的不好,查询效率低
但你设计再好,也很难达到完全平均
为此我们必须要改进Hashmap,下面介绍LinkedHashmap,Treemap
(二)LinkedHashmap
LinkedHashmap继承了Hashmap,就是添加双向指针
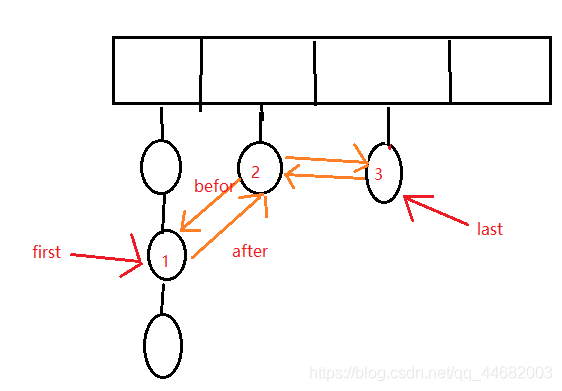
图画的不太好,大家可以看懂就行,图中的红色数字:1,2,3代表的是插入顺序,那就是用双向链表结构把插入顺序的节点串起来,其实就是维护一个插入顺序,遍历顺序其实就是插入顺序:维护了插入顺序+hashmap的特点
我的做法是先完成hashmap源码的添加,删除,在此基础添加几个指针就好,完成指向关系,最终实现如下:
//1、模拟源码实现Hashmap
//2、在Hashmap基础上实现LinkedHashmap
public class MyHashmap {
private Entry[] table = new Entry[16];
static final Entry[] EMPTY_TABLE = {};
private static final int DEFAULT_CAPACITY = 1<<4;
float threshold = 0.75f;//加载因子
//加载因子越大扩容的时机越晚 ,哈希冲突发生的概率越大,空间利用率越高
//加载因子越小扩容的时机越早 ,哈希冲突发生的概率越低,空间利用率越低
private int size;
private Entry last;//只想最有一个节点
private Entry first;//指向第一个节点,这两个指针为了LinkedHashmap插入正确性,底下写show方法
int modCount;
public MyHashmap() {
//此处传一个空数组
table = EMPTY_TABLE;
}
public static class Entry {
Entry before, after;
K key;
V value;
Entry next;
int hash;
public Entry(int hash,K key, V value, Entry next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
@Override
public String toString() {
return "Entry{" +
"key=" + key +
", value=" + value +
'}';
}
}
private class HashIterator implements Iterator>{
Entry next;//保存的下一要被遍历的节点
int index;//当前遍历的节点下标
Entry current;//保存当前节点
int expectedModcount = modCount;
public HashIterator() {
//next指向下一节点
if (size>0){
Entry [] t = table;
//寻找第一个不为空的节点在哪
while (index next() {
if (modCount!=expectedModcount){
throw new ConcurrentModificationException();
}
//返回当前节点,让next指向下一节点
Entry e = next;
//让next只想下一节点
next = next.next;
if (next == null){
Entry [] t = table;
//寻找第一个不为空的节点在哪((这个方法很妙)
while (index> iterator(){
return new HashIterator();
}
//返回hash(key) = index
public int hash(K Key) {
if (Key == null){
return 0;
}
return Key.hashCode();
}
public int indexOf(int hash,int length){
return hash & (length-1);
}
//加入元素
public V put(K key, V value) {
//第一次添加数据:对数组进行初始化
if (table == EMPTY_TABLE){
table = new Entry[DEFAULT_CAPACITY];
}
//通过key得到index
int hash = hash(key);
int index = indexOf(hash,table.length);
//1:key为空情况
if (key==null){
return putForNullKey(hash,value);
}
//2:key不为空(key是否重复)
//key重复
for (Entry e = table[index];e !=null;e = e.next){
/**
* 对象的hashcode相当于人名,hashcode相同并不能说明就是同一个人
*/
if (e.hash == hash && (e.key == key|| e.key.equals(key))){//说明重复
V entry = e.value;
e.value = value;
return entry;
}
}
//判断扩容
if (size>=table.length*threshold && (null!=table[0])){
//二倍扩容
resize();
index = indexOf(hash,table.length);
}
//头插法
Entry head = table[index];
Entry newEntry = new Entry<>(hash,key, value, head);
table[index] = newEntry;
//这里判断,可能添加第一个元素
if (last!=null){
last.after = newEntry;
newEntry.before = last;
last = newEntry;
}else {
last = newEntry;
first = newEntry;
}
size++;
modCount++;
return newEntry.value;
}
//二倍扩容
public void resize(){
int oldlength = table.length;
int newlength = oldlength<<1;
Entry[] newtable = new Entry[newlength];
for (Entry e:table){//遍历原数组
while (null!=e){
Entry next = e.next;
int i = indexOf(e.hash,newlength);
e.next = newtable[i];//x
newtable[i] = e;
e = next;
}
}
table = newtable;
}
//key为空时候的添加元素情况,并且返回旧值
private V putForNullKey(int hash,V value) {
/**
* 两种情况:本来就有和没有null
*/
//1:若本来就存在key==null
for (Entry e = table[0];e !=null;e = e.next){
if (e.key == null){//说明重复
V entry = e.value;
e.value = value;
return entry;
}
}
//判断扩容
if (size>=table.length*threshold && (null!=table[0])){
//二倍扩容
resize();
}
//2:说明没有重复元素,返回值就好
Entry head = table[0];
Entry newEntry = new Entry<>(hash,null, value, head);
table[0] = newEntry;
if (last!=null){
last.after = newEntry;
newEntry.before = last;
last = newEntry;
}else {
last = newEntry;
first = newEntry;
}
size++;
modCount++;
return newEntry.value;
}
public V remove(K key){//注意和删除时候可能要更新first和last节点,分类讨论
//两种情况:key为空和不为空
//1:key为空
if(key == null){
return removeForNullKey(key);
}
//通过key得到index
int hash = hash(key);
int index = indexOf(hash,table.length);
//key不为空时候删除
Entry e = table[index];
//头删除
/**
* 注意:重写eqlues必须重写hashcode
*/
if (e.hash == hash && (e.key == key|| e.key.equals(key))){
removeFL(e);
Entry entry = e.next;
V value = e.value;
table[index] = entry;
size--;
modCount--;
return value;
}else {
//非头部删除
while (e.next!=null){
if (e.next.key.equals(key)){
removeFL(e.next);
Entry entry = e.next.next;
V value = e.value;
e.next = entry;
size--;
modCount--;
return value;
}else {
e = e.next;
}
}
}
return null;
}
//key为空时候的删除情况
private V removeForNullKey(K key) {
//注意头部删除也要更新first指针
//头部删除
Entry head = table[0];
if (head.key == null){
removeFL(head);
Entry next = head.next;
V value = head.value;
table[0] = next;
size--;
modCount--;
return value;
}
//非头部删除
while (head.next!=null){
if (head.next.key==null){
removeFL(head.next);
Entry next = head.next.next;
V value = head.next.next.value;
head.next = next;
size--;
modCount--;
return value;
}
}
return null;
}
//删除时候对last和first调整
public void removeFL(Entry entry){
if (size==1){
last = first = null;
}else if (first == entry){
first = first.after;
}else if (last == entry){
last = last.before;
}else {
entry.before.after = entry.after;
entry.after.before = entry.before;
}
}
public void show (){
while (first!=null){
System.out.println(first);
first = first.after;
}
}
(三)TreeMap
TreeMap存储Key-value结构,key-value的存储位置是根据key的大小排序的来的
底层数据结构:红黑树(关于红黑树性质,代码实现,在我别的博客里)
TreeMap的增删改查就是:红黑树的增删改查操作