2022牛客寒假算法基础集训营 4(四) 全部题解
文章目录
- A R 模拟
- B 进制 线段树
- C 蓝彗星 前缀和
- D 雪色光晕 计算几何
- E 真假签到题 签到
- F 小红的记谱法 模拟
- G 子序列权值乘积 数学
- H 真真真真真签到题 签到
- I 爆炸的符卡洋洋洒洒 背包dp
- J 区间合数的最小公倍数 数学
- K 小红的真真假假签到题题 签到
- L 在这冷漠的世界里光光哭哭 dp【待补】
- 总结
比赛链接
题解https://ac.nowcoder.com/discuss/835616?type=101&channel=-1&source_id=0
A R 模拟
题目链接
题意:
给一个包含只包含大写字母的字符串,找有多少个子串包含 k k k 个 R R R 字符且不包含 P P P 字符

题解:
不包括 P P P 就分段来计算
至少包含 k k k 个 R R R
贡献就等于这个位置 第前 k 个 R R R 位置
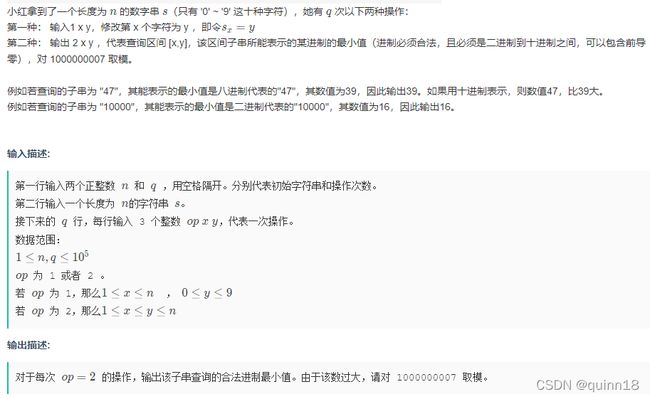
#includeB 进制 线段树
题解:
所能表示的某进制的最小值的某进制就是该串里的最大的数字+1,不然那个数不可能出现
题目要求单点修改和区间查询
那就是最简单的求最大值和求和的线段树板子
求和的线段树是存了2-10进制棵每一位的数字 * 该位权值
比如10进制树 123存的是1 * 10 * 10 ------- 2*10 -------3
求和出来还要除与多的权值 取[1,2] ,答案等于120/10
#include
}
}
build(1, 1, n);
for(int i=2; i<=10; i++) build1(1, 1, n, i);
//cout<<"$$$"<
while(q--) {
int op, x, y;
cin>>op>>x>>y;
if(op==1) {
update(1, 1, n, x, y);
for(int i=2; i<=10; i++) update1(1, 1, n, x, y*ksm(i, n-x), i);
}else {
int dang=query(1, 1, n, x, y);
if(dang==0) cout<<0<<endl;
else {
dang++;
cout<<query1(1,1,n,x, y,dang)%M*ksm(ksm(dang, n-y), M-2)%M<<endl;//逆元
}
}
}
return 0;
}
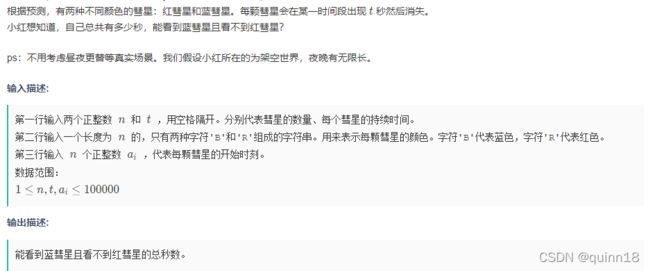
C 蓝彗星 前缀和
题解:
前缀和求覆盖次数
#include
}
int ans=0;
for(int i=1; i<=N; i++) {
if(b[i]&&!c[i]) ans++;
}
cout<<ans<<endl;
return 0;
}
D 雪色光晕 计算几何
题目链接
题意:
题解:
求点到线段的最短距离板子
#includeE 真假签到题 签到
题目链接
题意:
那个函数就是求本身
题解:
要开longlong
#includeF 小红的记谱法 模拟
题目链接
题意:
模拟
题解:
模拟
#includeG 子序列权值乘积 数学
题目链接
题意:
求这个数组的所有 非空子序列 的最大值*最小值的乘积是多少?
1e5
题解:
先排序
若它作为一个字序列的最小值,后面的 n − i n-i n−i 个数随意,也就是有 2 的 n − i 2的n-i 2的n−i 次方 个机会作为最小值,同样的,有 2 的 i − 1 2的 i-1 2的i−1次方 个机会作为最小值,那这个数产生的贡献就是
幂次取模的话取 M o d − 1 Mod-1 Mod−1
证明如下

#includeH 真真真真真签到题 签到
题目链接
题意:
题解:
就是把距离当成体对角线来算体积
因为小紫肯定在正方体中间
#includeI 爆炸的符卡洋洋洒洒 背包dp
题目链接
题意
题解
d p [ i ] [ j ] dp[i][j] dp[i][j] 代表轮到第 i i i张卡时候的质量% k = = j k==j k==j的最大值
转移方程
i n t p = ( j − a [ i ] + k ) int p=(j-a[i]+k) intp=(j−a[i]+k)%k
d p [ j ] [ i ] = m a x ( d p [ j ] [ i − 1 ] , d p [ j ] [ i ] ) ; dp[j][i]=max(dp[j][i-1], dp[j][i]); dp[j][i]=max(dp[j][i−1],dp[j][i]);不取当前牌
d p [ j ] [ i ] = m a x ( d p [ p ] [ i − 1 ] + b [ i ] , d p [ j ] [ i ] ) ; dp[j][i]=max(dp[p][i-1]+b[i], dp[j][i]); dp[j][i]=max(dp[p][i−1]+b[i],dp[j][i]); 取当前牌
#includeJ 区间合数的最小公倍数 数学
题目链接
题意:
#includeK 小红的真真假假签到题题 签到
题目链接
题意:
题解:
101变成101101
就等于乘(2的幂次+1)一定是倍数且1的个数不同
#includeL 在这冷漠的世界里光光哭哭 dp【待补】
题目链接
总结
Qwq