理解RNN和LSTM

  本文是台大李宏毅教授ML2020课程笔记。同时参考了其他博客。

网上关于RNN和LSTM的blogs太多了，本文只是摘抄+笔记。

1. RNN

  RNN（Recurrent Neural Network）是一类用于处理序列数据的神经网络。所谓序列，通常除了数据维度以外，还存在广义的时间维度，即序列是有顺序的，反应了数据随着时间的变化状态，例如，一串语音信号、一段文本或者一段视频都是序列。

1.1 RNN结构

  传统的前馈神经网络包含输入层、输出层和隐藏层，通过激活函数控制输出，层与层之间通过权值相连。神经网络训练的过程即是学习这些权重向量。
  与基础的NN不同，RNN不仅有多层，且也有激活函数和权值向量，其最大的区别在于，RNN在同一层的神经元之间也存在权值连接，如下图：

  在上面的图中，神经网络的模块，$A$，正在读取某个输入 $x_i$，并输出一个值 $h_i$ 。循环可以使得数据可以从当前步传递到下一步。
在时间维度上将上图展开：

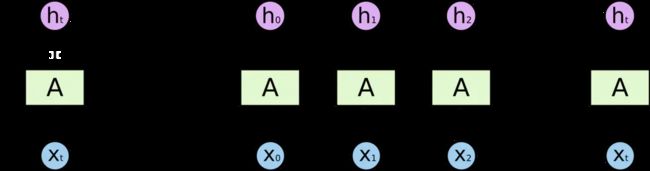
  RNN 可以被看做是同一神经网络的多次复制，每个神经网络模块会把消息传递给下一个。特别注意上述并不是传统NN的多个神经元，而是同一个神经元在时间维度上的展开，其本质还是一个神经元。
   RNN的基本结构便是这样，我们可以通过堆叠多个模块 $A$ (其实就是权值矩阵)来实现多层RNN网络。
   为了说明方便，我们设定一个slot filling问题，要求给定一句话，如

I would like to arrive Taipei on November 2nd.

  机器能够分别出句子中的信息：

Destination:Taipei
time of arrival:November 2nd

  据此构建的RNN网络如下：

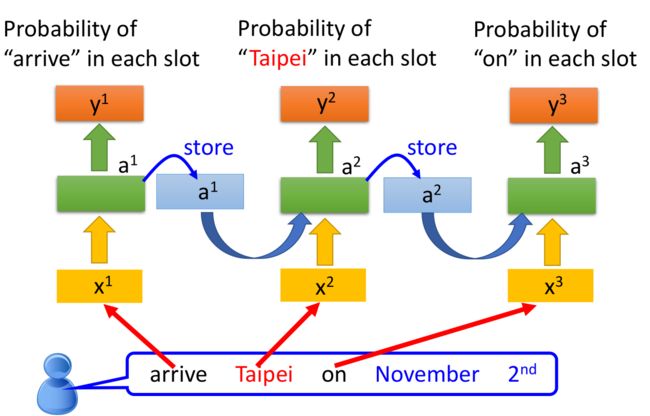
  图中，当 $x^1$ arrive 输入后，模块 $A$ 返回 $a^1$ 并存储在 $A$ 中，当序列的下一个数据 $x^2$ Taipei到达时，模块 $A$ 根据上一次的结果 $a^1$ 和当前的输入 $x^2$ 来决定当前的输出 $a^2$ 和 $y^2$（$y^2$ 是根据 $a^2$ 得到的）。

1.2 模块 $A$ 的内部结构

  为了更深入理解RNN的具体工作原理以及后面back-propagation 的推导，有必要从数学上知道整个RNN的工作过程。我们将上图RNN的结构更详细的表示成：

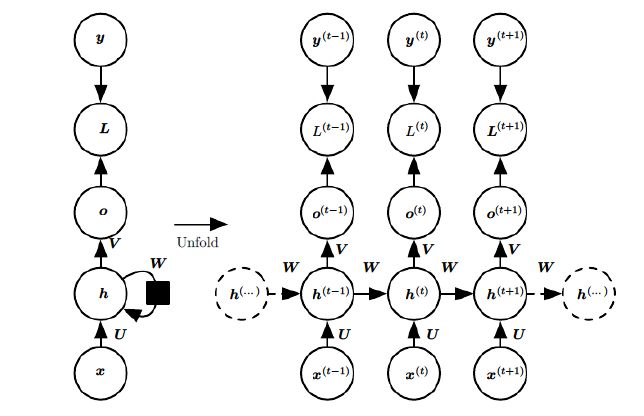
  这是一个标准的RNN结构图，图中每个箭头代表做一次变换，和之前一样，左侧是折叠起来的样子，右侧是展开的样子。我们可以很清楚的知道模块 $A$ 包含了哪些结构。图中，$x$ 代表输入向量，$U、V、W$代表将要学习的权值矩阵，$o$ 代表输出，$y$ 代表样本给出的确定值（即标签），元素右上角带的 $t$ 代表 $t$ 时刻的状态（或者说，序列中的第 $t$ 个元素），$L$ 代表损失函数，我们可以看到，损失也是随着序列的推进而不断积累的。

1.3 标准RNN的前向传播过程

  有了以上结构，RNN的 feed-forward过程如下。对于 $t$ 时刻，有：
$$h^{(t)}=\varphi \left(U{x}^{(t)}+W{h}^{(t-1)}+b\right)$$

这里的 $h^{(t)}$ 和前文例子中的 $a^t$ 一样，只不过来自于不同的资料，数学符号表示不同。

  其中 $\varphi ()$ 为激活函数，一般来说会选择 tanh 函数，$b$ 为偏置。
显然，$t$ 时刻的输出如下：
$$o^{(t)}=V{h}^{(t)}+c$$
  最终模型的预测输出为：
$$y^{(t)}=\sigma \left(o^{(t)}\right)$$
  其中 $\sigma ()$ 为激活函数，通常RNN用于分类，故这里一般用 softmax 函数。

1.4 RNN的训练方法——BPTT

  BPTT（back-propagation through time）算法是常用的训练RNN的方法，其实本质还是BP算法，只不过RNN处理时间序列数据，所以要基于时间反向传播，故叫随时间反向传播。BPTT的中心思想和BP算法相同，沿着需要优化的参数的负梯度方向不断寻找更优的点直至收敛，因此仍需要求各个参数的梯度。

1.4.1 chain rule 回顾

  考虑函数 $z=f(x,y)$, 其中 $x=g(t),y=h(t),g(t)$ 和 $h(t)$ 是可微函数, 那么:
$$\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}$$
  假设 $z=f(u,\nu )$ 的每一个自变量都是二元函数, 也就是说, $u=h(x,y),V=g(x,y)$, 且这些函数都是可微的。那么, $z$ 的偏导数为:
$$\begin{array}{rl}& \frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x}\\ & \frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y}\end{array}$$

1.4.2 BPTT

  观察 1.2 中的结构，需要寻优的参数有三个，分别是 $U、V、W$ 。与BP算法不同的是，其中 $W$ 和 $U$ 两个参数的寻优过程需要追溯之前的历史数据，参数 $V$ 相对简单只需关注目前，那么我们就来先求解参数 $V$ 的偏导数：
$$\frac{\partial L^{(t)}}{\partial V}=\frac{\partial L^{(t)}}{\partial o^{(t)}}\cdot \frac{\partial o^{(t)}}{\partial V}$$

因为 $V$ 是与时间无关的参数，所有没有角标 $t$。

  其中，$L^t$ 代表了时刻 $t$ 的损失函数，而总的损失函数是所有时刻的损失函数求和：
$$L=\sum _{t=1}^n{L}^{(t)}$$
  因此，最终损失函数 $L$ 对 $V$ 的梯度如下：
$$\frac{\partial L}{\partial V}=\sum _{t=1}^n\frac{\partial L^{(t)}}{\partial o^{(t)}}\cdot \frac{\partial o^{(t)}}{\partial V}$$
  其中，$\frac{\partial L^{(t)}}{\partial o^{(t)}}$ 取决于损失函数的定义，$\frac{\partial o^{(t)}}{\partial V}=h^{(t)}$。$W$ 和 $U$ 的偏导的求解由于需要涉及到历史数据，其偏导求起来相对复杂，我们先假设只有三个时刻，那么在第二个时刻 $L$ 对 $W$ 的偏导数为：
$$\frac{\partial L^{(2)}}{\partial W}=\frac{\partial L^{(2)}}{\partial o^{(2)}}\frac{\partial o^{(2)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial W}+\frac{\partial L^{(2)}}{\partial o^{(2)}}\frac{\partial o^{(2)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial h^{(1)}}\frac{\partial h^{(1)}}{\partial W}$$
  同理，该时刻 $L$ 对 $U$ 的偏导数为：
$$\frac{\partial L^{(2)}}{\partial U}=\frac{\partial L^{(2)}}{\partial o^{(2)}}\frac{\partial o^{(2)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial U}+\frac{\partial L^{(2)}}{\partial o^{(2)}}\frac{\partial o^{(2)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial h^{(1)}}\frac{\partial h^{(1)}}{\partial U}$$
  在第三个时刻，有：
$$\frac{\partial L^{(3)}}{\partial W}=\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial W}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial W}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial h^{(1)}}\frac{\partial h^{(1)}}{\partial W}$$
$$\frac{\partial L^{(3)}}{\partial W}=\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial W}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial W}+\frac{\partial L^{(3)}}{\partial o^{(3)}}\frac{\partial o^{(3)}}{\partial h^{(3)}}\frac{\partial h^{(3)}}{\partial h^{(2)}}\frac{\partial h^{(2)}}{\partial h^{(1)}}\frac{\partial h^{(1)}}{\partial W}$$
  而为了求出整个损失函数 $L$ 对 $W、U$ 的偏导数，我们需要对损失函数求和。观察上式，我们可以发现规律如下：
$$\begin{array}{rl}& \frac{\partial L^{(t)}}{\partial W}=\sum _{k=1}^t\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}\left(\prod _{j=k+1}^t\frac{\partial h^{(j)}}{\partial h^{(j-1)}}\right)\frac{\partial h^{(k)}}{\partial W}\\ & \frac{\partial L^{(t)}}{\partial U}=\sum _{k=1}^t\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}\left(\prod _{j=k+1}^t\frac{\partial h^{(j)}}{\partial h^{(j-1)}}\right)\frac{\partial h^{(k)}}{\partial U}\end{array}$$
  其中，${\prod }_{j=k+1}^t$ 当 $j=k+1>t$ 时值为1。
  整体的偏导公式就是将其按时刻再一一加起来。可以看出，中间的累乘部分：
$$\prod _{j=k+1}^t\frac{\partial h^{(j)}}{\partial h^{(j-1)}}=\prod _{j=k+1}^t{f}^{\prime }\cdot W_s$$
  $f()$ 代表激活函数，可选 $\tanh$ 或者 $sigmoid$ ，而由于这两个函数的导数都非常小（且小于 $1$），累乘之后将接近于 $0$，从而导致整个梯度接近于零，这种现象被称为梯度消失。
  解决梯度消失是非常重要的，否则网络将收敛地很慢，常用的改善方法为：

• 选取更好的激活函数，例如 ReLU，该函数在大于零时的导数为 $1$，这就避免了小数的连乘，一定程度上改善了梯度消失。
• 改变传播结构。

2. LSTM

2.1 Why LSTM

  RNN 的关键之一就是他们可以用来连接先前的信息到当前的任务上。例如，我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the ____” 最后的词，我们并不需要任何其他的上下文 —— 因为下一个词很显然就应该是 sky。在这样的场景中，相关的信息和预测的词位置之间的间隔是非常小的，RNN 可以学会使用先前的信息。但是同样会有一些更加复杂的场景。假设我们试着去预测“I grew up in France… I speak fluent ____”最后的词（…表示中间还有一些其他的句子）。当前的信息建议下一个词可能是一种语言的名字，但是如果我们需要弄清楚是什么语言，我们是需要先前提到的离当前位置很远的 France 的上下文的。不幸的是，正如前文所言，在这个间隔不断增大时，RNN对远处信息的学习能力大幅下降。
  因此，Hochreiter & Schmidhuber (1997) 等人于1997年就提出了LSTM 网络，并且在接下来的工作中被许多人改进和推广。LSTM 在各种各样的问题上表现非常出色，现在被广泛使用。它被明确设计用来避免长期依赖性问题。长时间记住信息实际上是 LSTM 的默认行为，而不是需要努力学习的东西。

2.2 LSTM结构

  首先回顾一下在RNN的前向传播结构中，模块 $A$ 中的内容可以用数学公式表示为：
$$h^{(t)}=\varphi \left(U{x}^{(t)}+W{h}^{(t-1)}+b\right)$$
  即通过一个 tanh 层实现重复的模块：

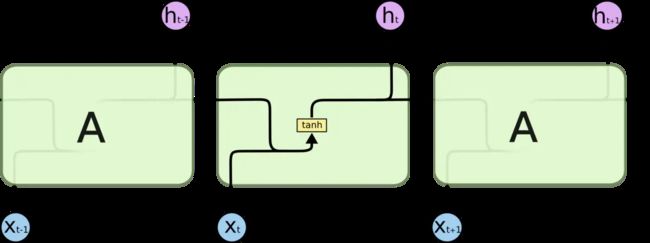
  LSTM 同样是这样的结构，但是重复的模块拥有一个不同的结构。不同于 单一神经网络层，这里是有四个，以一种非常特殊的方式进行交互：

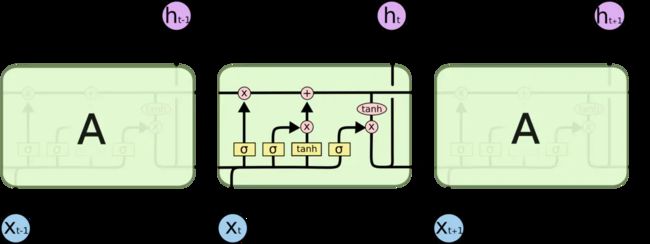
  先来熟悉一下图中使用的各种元素的图标：

  在上面的图例中，每一条黑线传输着一整个向量，从一个节点的输出到其他节点的输入。粉色的圈代表 pointwise （对应元素）的操作，而黄色的矩阵就是学习到的神经网络层。合在一起的线表示向量的连接，分开的线表示内容被复制，然后分发到不同的位置。
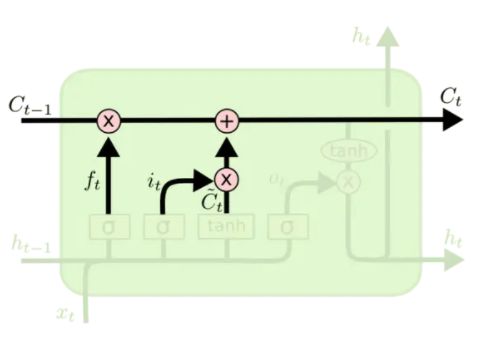
  LSTM 内部的本质还是矩阵向量乘法和激活函数计算，为了方便理解，将 LSTM 的内部结构分成三个门（gate），分别是 input gate、forget gate 和 output gate。图中的 $\sigma ()$ 都是指 sigmoid 函数，取值显然是 $0$ 到 $1$，用来表示该gate对数据的控制作用，0 代表“不许任何量通过”，1 就指“允许任意量通过”。

forget gate

  LSTM 中，模块上方的水平线就代表了这个模块的 memory，即下图的 $C_{t-1}、C_t$ ：

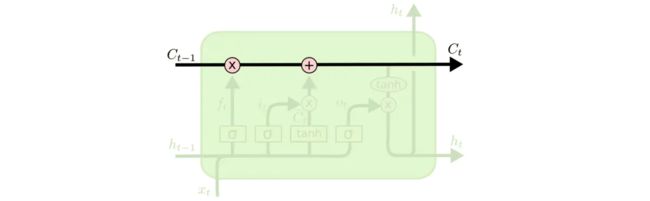
  forget gate用来决定上一时刻模块中的 memory 的保留程度

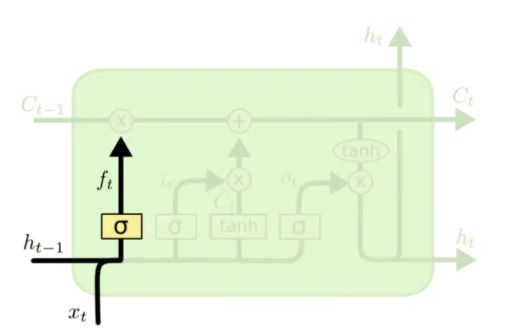
  首先 sigmoid 函数的输出为：
$$f_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)$$
  其中，$W_f、b_f$ 为forget gate 的权值矩阵和向量，$h_{t-1}$ 为上一时刻该模块（神经元）的输出，$x_t$ 为 $t$ 时刻输入。通过 sigmoid 函数的结果 $f_t$ 和 上一时刻模块的 memory $C_{t-1}$ 相乘，决定我们会从模块中丢弃什么信息。例如，当我们看到一个长句子新的主语，我们希望忘记旧的主语。

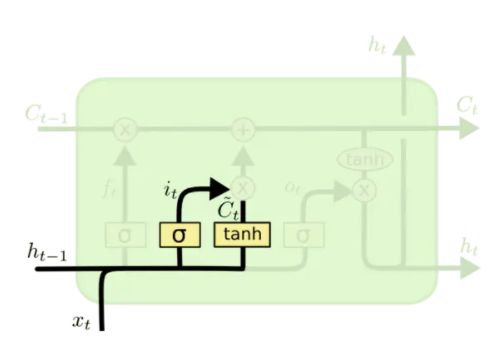
input gate

  下一步是确定什么样的新信息被存放在模块中。这里包含两个部分。第一，sigmoid 层决定什么值将要更新。然后，一个 tanh 层创建一个新的向量（memory），${\tilde{C}}_t$，会被加入到该模块中。下一步，将这两个信息来产生对状态的更新：
$$\begin{array}{rl}{i}_t& =\sigma \left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)\\ {\tilde{C}}_t& =\tanh \left(W_C\cdot \left[h_{t-1},x_t\right]+b_C\right)\end{array}$$
  此时输入数据以及处理完毕。这里的$W、b$ 同样代表要被学习的权值矩阵和向量。

output gate

  最后在 output gate 中，首先更新模块的 memory，并输出该模块该时刻最终的处理结果 $h_t$，：
$$\begin{array}{rl}{C}_t^{\prime }& =i_t\cdot {\tilde{C}}_t\\ C_t& =C_t^{\prime }+f_t\cdot C_{t-1}=i_t\cdot {\tilde{C}}_t+f_t\cdot C_{t-1}\\ o_t& =\sigma \left(W_o\left[h_{t-1},x_t\right]+b_o\right)\\ h_t& =o_t\ast \tanh \left(C_t\right)\end{array}$$

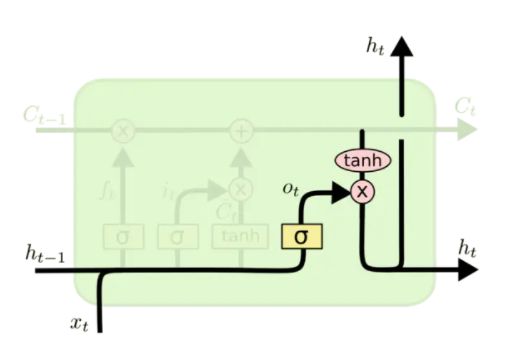
  通过一个 sigmoid 函数来决定该层的输入 $x_t$ 和上一层的输出 $h_{t-1}$ 对该层的输出的影响。而通过一个 tanh 函数对更新后的 memory 进行处理，得到一个在 $-1$ 到 $1$ 之间的值，两者相乘得到最终的输出部分。

  以上便完成了LSTM的cell的计算过程。

3. pytorch中的RNN 和 LSTM module

3.1 torch.nn.RNN()

  pytorch中的RNN模块实现了一个多层的RNN结构，其数学表示如下：
$$h_t=f\left(W_{ih}{x}_t+b_{ih}+W_{hh}{h}_{(t-1)}+b_{hh}\right)$$
  其中，$h_t$ 为 $t$ 时刻隐藏层的状态，$x_t$ 为 $t$ 时刻的输入，$f$ 只能是 $\tanh$ 或者 sigmoid 函数。其参数如下：

• input_size - 输入 $x$ 中特征的数量，即向量 $x$ 的维度，并不是指序列的长度。必须给定
• hidden_​​size - 隐藏状态 $h$ 的特征数，即隐藏层中节点的个数。必须给定
• num_layers - 循环层数，即前文所述的模块 $A$ 向上堆叠的层数，必须给定
• nonlinearity - 输出激活函数，可选’tanh’ 或 ‘relu’。 默认: ‘tanh’
• bias - 如果False，则该层不使用偏差权重 $b_{ih}$ 和 $b_{hh}$ 。默认：True
• batch_first – 如果True，则输入和输出张量作为(batch, seq, feature)而不是(seq, batch, feature) 提供。默认：False
• dropout - 如果非零，则在除最后一层之外的每个 RNN层的输出上引入一个Dropout层。默认值：0
• bidirectional - 如果True，则是双向 RNN。默认：False

  网络的输入数据解释如下：

• input - 形如 $\left(L,N,H_{in}\right)$ 的 Tensor 当 batch_first=False，或者 $\left(N,L,H_{in}\right)$ 的 Tensor 当 batch_first=True.
• h_0 - 形如 $\left(D\ast \text{num\_layers},N,H_{\text{out}}\right)$ 的 Tensor，给出隐藏层的初始状态。

其中：
$$\begin{array}{rl}N& =\text{ batch size }\\ L& =\text{ sequence length }\\ D& =2\text{ if bidirectional }=\text{ True otherwise }1\\ H_{\text{in }}& =\text{ input\_size }\\ H_{\text{out }}& =\text{ hidden\_size }\end{array}$$

  网络的输出数据解释如下：

• output - 形如 $\left(L,N,D\ast H_{\text{out }}\right)$ 的 Tensor 当 batch_first=False，或者 $\left(N,L,D\ast H_{\text{out }}\right)$ 的 Tensor 当 batch_first=True.
• h_n - 形如 $\left(D\ast \text{num\_layers},N,H_{\text{out}}\right)$ 的 Tensor，给出隐藏层的最终状态。

  用例：

rnn = nn.RNN(10, 20, 2) # input_size = 10; hidden_size = 20; num_layers = 2
input_ = torch.randn(5, 3, 10) # sequence length = 5; batch size = 3; input_size = 10;
h0 = torch.randn(2, 3, 20) # D = 1; D∗num_layers = 2; batch size = 3; hidden_size = 20;
output, hn = rnn(input_, h0)

  最后，关于 input_size 、hidden_size 和 sequence length 这几个量，首先想象一个普通的神经网络如下图，

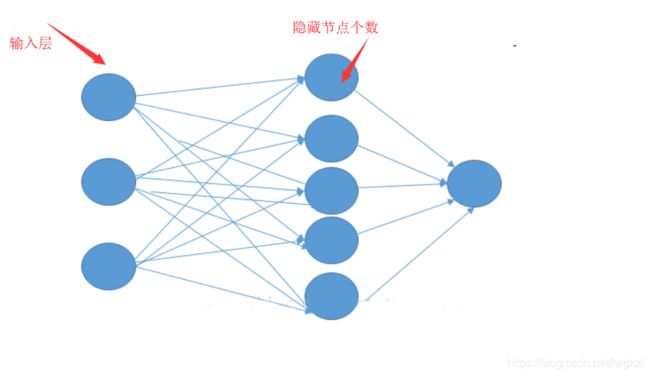
  我们将这个图贴在xz平面，并且向y轴方向复制，那么复制的次数就是序列的长度 sequence length，此时相当于RNN沿着时间维度扩展（权值矩阵相同，因为是复制过去的），而 input_size 就是图中输入层节点的数量，或者说是输入向量 $x_i$ 的维度，hidden_size 就是隐藏节点的个数，例如，在下图中：

  图被复制了三次，那么sequence length = 3，而显然 input_size = 3，hidden_size = 5。

3.2 torch.nn.LSTM()

  lstm里，层与层之间传递的是输出 $h_t$ ，同一层内传递的细胞状态（即memory）$C_i$，导致它和RNN有一些区别。
同理，我们写出LSTM的运算过程如下：
$$\begin{array}{rl}{i}_t& =\sigma \left(W_{ii}{x}_t+b_{ii}+W_{hi}{h}_{t-1}+b_{hi}\right)\\ f_t& =\sigma \left(W_{if}{x}_t+b_{if}+W_{hf}{h}_{t-1}+b_{hf}\right)\\ g_t& =\tanh \left(W_{ig}{x}_t+b_{ig}+W_{hg}{h}_{t-1}+b_{hg}\right)\\ o_t& =\sigma \left(W_{io}{x}_t+b_{io}+W_{ho}{h}_{t-1}+b_{ho}\right)\\ c_t& =f_t\odot c_{t-1}+i_t\odot g_t\\ h_t& =o_t\odot \tanh \left(c_t\right)\end{array}$$
  其中，各种变量和前文所述一样，$\odot$ 代表 element-wise product。网络的参数如下：

• input_size - 输入 $x$ 中特征的数量，即向量 $x$ 的维度，并不是指序列的长度。必须给定
• hidden_​​size - 隐藏状态 $h$ 的特征数，即隐藏层中节点的个数。必须给定
• num_layers - 循环层数，即前文所述的模块 $A$ 向上堆叠的层数，必须给定
• nonlinearity - 输出激活函数，可选’tanh’ 或 ‘relu’。 默认: ‘tanh’
• bias - 如果False，则该层不使用偏差权重 $b_{ih}$ 和 $b_{hh}$ 。默认：True
• batch_first – 如果True，则输入和输出张量作为(batch, seq, feature)而不是(seq, batch, feature) 提供。默认：False
• dropout - 如果非零，则在除最后一层之外的每个 RNN层的输出上引入一个Dropout层。默认值：0
• bidirectional - 如果True，则是双向 RNN。默认：False
• proj_size - 如果大于 0，将使用具有相应大小投影的LSTM。默认：0

  网络的输入数据解释如下：

• input - 形如 $\left(L,N,H_{in}\right)$ 的 Tensor 当 batch_first=False，或者 $\left(N,L,H_{in}\right)$ 的 Tensor 当 batch_first=True.
• h_0 - 形如 $\left(D\ast \text{num\_layers},N,H_{\text{out}}\right)$ 的 Tensor，给出隐藏层的初始状态。
• c_0 - 形如 $\left(D\ast \text{num\_layers},N,H_{\text{cell}}\right)$ 的 Tensor，给出cell的初始状态（初始的memory）。

其中：
$$\begin{array}{rl}N& =\text{ batch size }\\ L& =\text{ sequence length }\\ D& =2\text{ if bidirectional }=\text{ True otherwise }1\\ H_{\text{in }}& =\text{ input\_size }\\ H_{\text{cell}}& =\text{ hidden\_size }\\ H_{\text{out}}& =\text{proj\_size if proj\_size}>0\text{ otherwise hidden\_size}\end{array}$$

  网络的输出数据解释如下：

• output - 形如 $\left(L,N,D\ast H_{\text{out }}\right)$ 的 Tensor 当 batch_first=False，或者 $\left(N,L,D\ast H_{\text{out }}\right)$ 的 Tensor 当 batch_first=True.
• h_n - 形如 $\left(D\ast \text{num\_layers},N,H_{\text{out}}\right)$ 的 Tensor，给出隐藏层的最终状态。
• c_n - 形如 $\left(D\ast \text{num\_layers},N,H_{\text{cell}}\right)$ 的 Tensor，给出cell的最终状态（最终记忆的memory）。

  用例：

rnn = nn.LSTM(10, 20, 2)
input_ = torch.randn(5, 3, 10)
h0 = torch.randn(2, 3, 20)
c0 = torch.randn(2, 3, 20)
output, (hn, cn) = rnn(input_, (h0, c0))

4. Reference

1. 台大李宏毅ML2020课件-RNN (v2) Recurrent Neural Network
2. https://blog.csdn.net/zhaojc1995/article/details/80572098
3. 链式法则
4. 理解 LSTM 网络
5. http://deeplearning.net/tutorial/lstm.html
6. pytorch api
7. https://blog.csdn.net/lwgkzl/article/details/88717678