Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey 论文阅读笔记
本文是论文的阅读笔记。
Paper: A Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey
Author:
Naveed Akhtar (cor) ([email protected])
Ajmal Mian
Press: 2018 IEEE Access
Department: Department of Computer Science and Software Engineering, The University of Western Australia Crawley, WA 6009, Australia
摘要
深度学习是当下兴起的人工智能的核心,也推动了计算机视觉领域的应用。
但是近来的研究证明,深度学习对以对输入进行微小扰动导致模型做出错误的预测输出的对抗攻击具有脆弱性,严重影响了人工智能投入到实际应用中。
本文是第一篇计算机视觉领域基于深度学习的对抗攻击的综述。
1 引言
深度学习在包括计算机视觉在内的多个领域都取得了巨大的突破和成功,并已经在人们日常生活和一些安全相关的方方面面都进行了应用。
Szegedy et al. [22]首先发现了深度神经网络一个有趣的软肋:对图像做一个微小的扰动,尽管人类的视觉无法区分,但是深度学习分类器以高置信度做出了一个错误的判断。自此以后,该领域吸引了一大批研究者进入,来探究深度学习对抗攻击的攻击和防御。
2 术语的定义
- Adversarial example/image 对抗样本、图片
对原始的图片做一个有目的的扰动(如引入噪音),使其能够迷惑机器学习技术,比如深度学习。 - Adversarial pertubation 对抗扰动
将噪音增加到原始样本中使其成为对抗样本的扰动 - Adversarial training 对抗训练
使用除了原始样本以外的对抗样本一起训练机器学习分类器 - Adversary 攻击者
创建对抗样本的人,有些时候指对抗样本本身 - Black-box attacks 黑盒攻击
一般指在对目标模型一无所知的条件下生成对抗样本,有些时候可指能获取少量模型信息 - White-box attacks 白盒攻击
目标模型的所有信息皆已知,包括参数值、模型结构、训练方法和训练数据等 - Detector 检测器
检测一个样本是否是对抗样本的机制 - Fooling ratio/rate 欺骗率
当扰动加到样本上后预测结果改变的比例 - One-shot/one-step methods 一步法
只需一步的计算即可生成对抗扰动,与高计算量的迭代法相对 - Quasi-imperceptible 基本不可察觉
微小地影响图片使人类无法察觉到 - Rectifier 修正器
恢复一个对抗样本的原始样本的分类标签 - Targeted attacks 目标攻击
使得分类器对对抗样本做出攻击者预定的分类标签的预测,与无目标攻击相对 - Threat model 威胁模型
潜在的攻击方法 - Universal perturbation 通用扰动
能迷惑一个检测器使其对不管什么图片都能误分的扰动 - Transferability 迁移性
某模型生成的对抗样本对其他模型也具有攻击效力
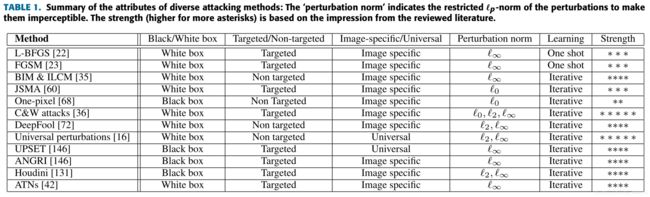
3 对抗攻击
3.1 针对分类的攻击
3.1.1 Box-constrained L-BFGS
Szegedy等[22]首先提出了微小的扰动能导致分类器误分的问题。
并给出了公式如下:
∥ m i n ρ ∥ 2 s . t . C ( I c + ρ ) = l ; I c + ρ ∈ [ 0 , 1 ] m \left\|min_\rho\right\|_2 s.t.\mathcal{C}(I_c+\rho)=l; I_c+\rho\in[0,1]^m ∥minρ∥2s.t.C(Ic+ρ)=l;Ic+ρ∈[0,1]m
其中,原始图片: I c ∈ R m I_c\in\mathbb{R}^m Ic∈Rm,扰动: ρ ∈ R m \rho\in\mathbb{R}^m ρ∈Rm,错误的标签: l l l,分类器: C ( ⋅ ) \mathcal{C}(\cdot) C(⋅)
由于难以求解,将其转换成可得解精确解的凸优化问题,使用L-BFGS的近似求解公式如下:
m i n ρ c ∣ ρ ∣ + L ( I c + ρ , l ) s . t . I c + ρ ∈ [ 0 , 1 ] m min_\rho c\left|\rho\right|+\mathcal{L}(I_c+\rho,l) s.t. I_c+\rho\in[0,1]^m minρc∣ρ∣+L(Ic+ρ,l)s.t.Ic+ρ∈[0,1]m
其中,求解分类器损失函数: L ( . , . ) \mathcal{L}(.,.) L(.,.)
3.1.2 Fast Gradient Sign Method (FGSM)
Goodfellow等[23]提出了有效生成对抗样本的方法:
ρ = ϵ s i g n ( ∇ J ( θ , I c , l ) ) \rho=\epsilon sign(\nabla \mathcal{J}(\theta,I_c,l)) ρ=ϵsign(∇J(θ,Ic,l))
其中,损失函数关于输入的导数: ∇ J ( . , . , . ) \nabla \mathcal{J}(.,.,.) ∇J(.,.,.),符号函数: s i g n ( . ) sign(.) sign(.),限制扰动大小的参数: ϵ \epsilon ϵ
此外,Miyato等[103]提出基于其的目标攻击:
ρ = ϵ ∇ J ( θ , I c , l ) ∥ ∇ J ( θ , I c , l ) ∥ 2 \rho=\epsilon\frac{\nabla\mathcal{J}\mathcal(\theta,I_c,l)}{\left\|\nabla\mathcal{J}\mathcal(\theta,I_c,l)\right\|_2} ρ=ϵ∥∇J(θ,Ic,l)∥2∇J(θ,Ic,l)
Kurakin[80]把上式称为’$Fast Gradient l 2 l2 l2‘,并提出了使用’ F a s t G r a d i e n t l ∞ Fast Gradient l\infty FastGradientl∞’
以上的这些都属于one-step或one-shot方法。
3.1.3 Basic & Least-likely-class Iterative Methods
The Basic Iterative Method (BIM)[35]使用的是迭代的思想:
I p i + 1 = C l i p ϵ { I p i + α s i g n ( ∇ J ( θ , I P i , l ) ) } I_p^{i+1}=Clip_\epsilon \{I_p^i+\alpha sign(\nabla\mathcal{J}(\theta,I_P^i,l))\} Ipi+1=Clipϵ{Ipi+αsign(∇J(θ,IPi,l))}
其中, C l i p ϵ { . } Clip_\epsilon \{.\} Clipϵ{.}在 ϵ \epsilon ϵ时削减了每个像素的值,且 α \alpha α决定每一步的步长。第i次扰动的图片: I p i + 1 I_p^{i+1} Ipi+1。
Madry等[55]指出此方法和一种叫梯度下降投影(Projected Gradient Descent)的标准凸优化方法相似。
与FGSM扩展到‘one-step target class’相似,Kurakin等[35]也将BIM扩展到’Iterative Least-likely Method’ (ILCM)。
3.1.4 Jacobian-based Saliency Map Attack (JSMA)
Papernot等[60]提出了通过限制 l 0 l_0 l0范数来生成对抗攻击的方法,这在物理上意味着一次只修改几个像素,而不是扰动整个图像。
该方法一次只扰动一个像素,并检查分类结果的变化情况。其可以进行目标攻击,并在每次选择一个最能迷惑网络的像素并改变它,以此反复迭代。
3.1.5 One Pixel Attack
对抗攻击的一个极端的例子是当仅仅一个像素发生改变就能够迷惑分类器。
Su等[68]人使用了差分进化(Differential Evolution)的方法,每次修改原图像的一个像素生成子图像,并通过比较选择保留,直到最后一张图,仅修改一个像素就可以对抗攻击。
这是一种黑盒攻击,唯一需要直到的就是目标分类器对样本的预测概率。
3.1.6 Carlini and Wagner Attacks (C&W)
Carlini和Wagner[36]提出了三种对抗攻击的方法,其对蒸馏防御(defensive distillation)有效。
该算法生成的扰动可以从unsecrued网络,迁移到secured网络上(有蒸馏),从而实现黑盒攻击。
受此启发,Chen等[41]提出了基于’Zeroth Order Optimization (ZOO)'的攻击。其直接估计目标模型的梯度来生成对抗样本。
3.1.7 DeepFool
Moosavi-Dezfooli等[72]提出使用迭代的方式来对给定的图片计算最小的规范对抗扰动,具体来说就是在每次迭代的时候用一个小的向量扰动图片使其逐渐被移除出被线性化的决策边界外。
作者证明他们的方法比FGSM的扰动小,但是却不失其性能。
3.1.8 Universarial Adversarial Perturbations
Moosavi-Dezfooli等[16]提出一种通用的对抗扰动方法,通用的扰动需满足下式:
P I c ℑ c ( C ( I c ) ≠ C ( I c + ρ ) ) ≥ δ s . t . ∥ ρ ∥ p ≤ ξ \mathop P\limits_{I_c~\Im_c}(\mathcal{C}(I_c)\ne\mathcal{C}(I_c+\rho))\ge\delta s.t. \left\|\rho\right\|_p\leq\xi Ic ℑcP(C(Ic)̸=C(Ic+ρ))≥δs.t.∥ρ∥p≤ξ
其中, P ( . ) P(.) P(.)是概率, δ \delta δ是欺骗率
作者使用和DeepFool相似的扰动方式,但是其是同时将所有的图片推到决策边界外。
3.1.9 Upset and Angri
Sarkar 等[145]提出了两种黑盒攻击算法,分别称为UPSET:Universal Perturbation for Steering to Exact Targets,和ANGRI:Antagonistic Network for Gnerating Rogue Images。
UPSET是特定类别目标的对抗攻击,不管什么图片都能使其误分为预定的类别,其解决如下优化问题:
I ρ = m a x ( m i n ( s R ( t ) + I c , l ) − l ) I_\rho=max(min(sR(t)+I_c,l)-l) Iρ=max(min(sR(t)+Ic,l)−l)
其中,像素值 I c I_c Ic被限制在[-1,1]内,s是一个标量,R(.)把目标类别t作为输入,并输出一个扰动R(t)。
ANGRI则是图像特定的扰动,思路相似。
两者都达到了较高的欺骗精度。
3.1.10 Houdini
Cisse等[130]提出了‘Houndini’一种欺骗基于梯度的机器学习方法的攻击方法。具体来说,就是根据模型的损失函数,利用网络的可微损失的梯度生成扰动。
3.1.11 Adversarial Transformation Networks (ATNs)
Baluja 和Fischer[42]训练前向神经网络来生成对抗样本来攻击一个或一组网络。被训练的模型被称为对抗变化网络(Adversarial Transformation Networks, ATNs)。
对抗样本通过最小化包含两部分的联合损失函数来生成:第一部分,使对抗样本和原始样本保持相似性;第二部分,使目标网络错分。
在相同的研究思路上,Hayex和Danezis[47]也使用攻击神经网络来进行黑盒攻击的对抗样本的生成。
在当下的结果显示,尽管上述方法能被察觉出来,但是它们的欺骗率是前所未有的高。
3.1.12 Miscellaneous(混杂的) Attacks
其他的攻击方法包括:
- Sabour等[26]提出和图像的分布式表达思路相似,可以通过改变表征图像类别的内部网络层来生成对抗样本。
- Papernot等[109]研究了对抗攻击对深度学习及其他机器学习模型的可迁移性,并引入更进一步的迁移攻击的思路。
- Narodytska和Kasiviswanathan[54]提出了仅改变图像中的几个像素点来欺骗神经网络的更进一步的黑盒攻击。
- Liu等[31]介绍了“epsilon近邻”这种能够以100%准确率欺骗蒸馏防御网络的白盒攻击方法。
- Oh等[132]从博弈论的角度研究了针对防御对抗的网络的攻击。
- Mpouri等[134]设计了与数据无关的方法来生成通用的对抗扰动。
- Hosseini等[98]引入了“语义对抗样本”的概念,以输入图像能与人类的语义相同但是会被错分为基础思路。
- Kanbak等[73]基于DeepFool方法的缺陷使用了“ManiFool”方法,用于评估神经网络对几何扰动的鲁棒性。
- Dong等[168]提出了一种迭代方法来提升黑盒攻击。
- Carlini和Wagner[49]说明了十种对抗的防御方法可以通过使用新的损失函数而失效。
- Rozsa等[94]提出了“热、冷”的方法,对一张图像生成多个可能的对抗样本。