图像的浅层特征与深度特征_图像LBP特征

LBP特征属于一种纹理特征，该算法在1996年由Ojala等提出，在2002年对算法进行了改进，提出了均衡模式LBP编码和旋转不变性LBP编码。该算法整体来说还是比较简单。但是，根据LBP编码之后的结果对图像进行分类的效果还是比较好。可以用于人脸分类，也可以用于其他对象的基于纹理特征的分类，通常采用LBP编码之后，需要对编码后的图像进行分块，计算每一块的直方图，然后将所有的直方图连接成一个大的直方图，其实就是一维向量。图像就用这个一维向量来表示。在进行分类的时候，可以采用SVM或者KNN等分类算法实现。

LBP的编码方式还是简单，图1是从原始论文中截图的编码示意图。具体的公式在这里就不详细介绍了，简单说一下方法。首先在图像上取一块邻域，比如3X3大小的区域，然后依次比较周围八个像素值与中间像素值的灰度值大小，如果大于等于中间像素值，则赋值为“1”，否则赋值为“0”。请见图1(a)和图1(b)。然后将得到的“1”和“0”连接起来，得到一个二进制串。至于这个二进制串从哪个位置开始，没有规定。对于同一幅图像，自己规定一个统一的起点就可以了。如图1(b),从右下角开始，按照顺时针方式得到的二进制串为“10111000”，然后将这个二进制串转换成十进制，为“169”，将这个值代替原来3X3邻域的中间位置的像素值。

图1 LBP算法编码示意

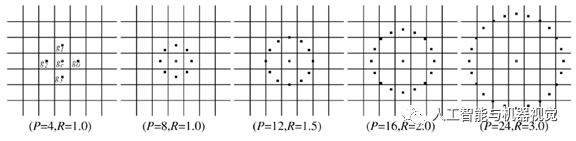
原始的LBP编码不具有旋转不变性，而且，容易受到噪声干扰。所以，研究者对该算法进行了很多改进。作者在2002年提出了改进的方法，首先将原来的3X3区域改成圆形区域，利用圆形边界上的点与中心点进行大小比较，圆形边界上的点采用插值得到。其次，作者分析了二进制串从“1”到“0”或从“0”到“1”的变化次数，发现图像上的特征对于每一个二进制串的变化次数一般不操作2次，因此得到均衡模式LBP编码，该编码方式只有58种编码结果。其他变化次数操作2次的都归为第59种。此外，还提出一种旋转不变编码方式，就是将得到的二进制串进行依次移位操作，只取得到的最大值最为编码结果，由此得到旋转不变性编码。图2是圆形LBP编码示意图，图3是旋转不变编码结果，这种方式只有36种编码值。

图2 圆形LBP邻域编码

图3 旋转不变性36种编码结果

LBP算法体现的是图像局部纹理特征，该算法自从提出来以后，在google学术上可以看得到引用次数已经上万次了，证明该算法确实有一定的效果。对其进行改进的算法也很多。Spring出版了两本关于LBP方面的书《Computer Vision Using Local Binary Patterns》和《Local Binary Patterns: New Variants and Applications》也足以说明该算法的影响力。

LBP算法为什么有效？从LBP编码的方式来看，其实该算法利用的也是图像的梯度关系。对于图像而言，梯度反映了图像的变化，而且，梯度一般不受光照变化的影响，梯度对于同一类型图像而言，其变化是很小的。所以，利用图像像素值之间的梯度关系可以实现图像分类。其实，很多与图像处理有关的算法，都离不开图像的梯度。LBP算法类似于计算了邻域像素与中心像素的梯度大小联合分布。因此，基于梯度的描述算子的判别性比较高，利用梯度关系进行图像分类一般效果都比较好。

LBP算法很简单，但是，如果在LBP上进行算法改进，还是有很多改进空间。如果想要在这方面发表几篇文章，还是很有机会的。LBP的原理很简单，下面以具体的代码来实现LBP编码，有需要的可以借鉴下，在opencv里面也有LBP的编码代码。

#include#include #include#include#include#includeusing namespace std;using namespace cv;///原始LBP编码void originLBP(Mat src,Mat dst){    for(int i=1;i-1;i++)    {        for(int j=1;j-1;j++)        {      unsigned char center = src.at(i,j);            unsigned char lbpCode = 0;            lbpCode |= (src.at(i-1,j-1) > center) << 7;            lbpCode |= (src.at(i-1,j  ) > center) << 6;            lbpCode |= (src.at(i-1,j+1) > center) << 5;            lbpCode |= (src.at(i  ,j+1) > center) << 4;            lbpCode |= (src.at(i+1,j+1) > center) << 3;            lbpCode |= (src.at(i+1,j  ) > center) << 2;            lbpCode |= (src.at(i+1,j-1) > center) << 1;            lbpCode |= (src.at(i  ,j-1) > center) << 0;            dst.at(i-1,j-1) = lbpCode;        }    }}template  staticinline void elbp_(InputArray _src, OutputArray _dst, int radius, int neighbors) {    //get matrices    Mat src = _src.getMat();    // allocate memory for result    _dst.create(src.rows-2*radius, src.cols-2*radius, CV_32SC1);    Mat dst = _dst.getMat();    // zero    dst.setTo(0);    for(int n=0; n  {        // sample points        float x = static_cast(radius * cos(2.0*CV_PI*n/static_cast(neighbors)));        float y = static_cast(-radius * sin(2.0*CV_PI*n/static_cast(neighbors)));        // relative indices        int fx = static_cast(floor(x));        int fy = static_cast(floor(y));        int cx = static_cast(ceil(x));        int cy = static_cast(ceil(y));        // fractional part        float ty = y - fy;        float tx = x - fx;        // set interpolation weights        float w1 = (1 - tx) * (1 - ty);        float w2 =      tx  * (1 - ty);        float w3 = (1 - tx) *      ty;        float w4 =      tx  *      ty;        // iterate through your data    for(int i=radius; i < src.rows-radius;i++)     {      for(int j=radius;j < src.cols-radius;j++)       {        // calculate interpolated value        float t = static_cast(w1*src.at<_tp>(i+fy,j+fx) + w2*src.at<_tp>(i+fy,j+cx) + w3*src.at<_tp>(i+cy,j+fx) + w4*src.at<_tp>(i+cy,j+cx));        // floating point precision, so check some machine-dependent epsilon        dst.at(i-radius,j-radius) += ((t > src.at<_tp>(i,j)) || (std::abs(t-src.at<_tp>(i,j)) < std::numeric_limits::epsilon())) << n;            }        }    }}static void elbp(InputArray src, OutputArray dst, int radius, int neighbors){    int type = src.type();    switch (type) {    case CV_8SC1:   elbp_(src,dst, radius, neighbors); break;    case CV_8UC1:   elbp_(src, dst, radius, neighbors); break;    case CV_16SC1:  elbp_(src,dst, radius, neighbors); break;    case CV_16UC1:  elbp_(src,dst, radius, neighbors); break;    case CV_32SC1:  elbp_(src,dst, radius, neighbors); break;    case CV_32FC1:  elbp_(src,dst, radius, neighbors); break;    case CV_64FC1:  elbp_(src,dst, radius, neighbors); break;    default:        string error_msg = format("Using Original Local Binary Patterns for feature extraction only works on single-channel images (given %d). Please pass the image data as a grayscale image!", type);    CV_Error(Error::StsNotImplemented, error_msg);        break;    }}//圆形LBPMat circularLBP(InputArray src, int radius, int neighbors) {    Mat dst;    elbp(src, dst, radius, neighbors);    return dst;}//计算跳变次数int getHopTimes(int n){    int count = 0;    bitset<8> binaryCode = n;    for(int i=0;i<8;i++)    {        if(binaryCode[i] != binaryCode[(i+1)%8])        {            count++;        }    }    return count;}///均衡模式LBP编码Mat uniformPatternLBP(Mat src,int radius,int neighbors){  Mat dst;  //建立映射表  uchar temp = 1;    uchar table[256] = {0};    for(int i=0;i<256;i++)    {        if(getHopTimes(i)<3)        {            table[i] = temp;            temp++;        }    }  //调用圆形LBP编码  Mat CircularDst = circularLBP(src, radius, neighbors);  //根据映射表重新确定dst的值  Mat dst_abs;  convertScaleAbs(CircularDst,dst_abs);//使用线性变换转换输入数组元素成8位无符号整型  //根据映射表重新确定dst的值  int rows = dst_abs.rows;  int cols = dst_abs.cols;  for(int i = 0;i   {    uchar* data = dst_abs.ptr(i);    for(int j = 0;j < cols;j++)    {      data[j] = table[data[j]];    }  }  convertScaleAbs(dst_abs,dst);//使用线性变换转换输入数组元素成8位无符号整型  return dst;}int* rotation_invariant_mapping(int range,int num_sp)//range=256,num_sp=8{  int newMax,rm,r;  int tmpMap[256];  int Mapping[256];   newMax = 0;  for (int i = 0 ; i < range ; i++)  {    rm = i;    r = i;    for (int j = 0 ; j < num_sp -1 ;j++)    {      //将r向左循环移动一位,当r超过num_sp位时，舍弃      r = r << 1;      if (r > range -1)      {        r = r - (range -1);      }      //printf("%d,%d\n",r,rm);      if (r < rm)      {        rm = r;      }    }    if (tmpMap[rm] < 0)    {      tmpMap[rm] = newMax;      newMax++;          }    Mapping[i] = tmpMap[rm];  }  return Mapping;}Mat rotationInvariantOfMapLBP(Mat img,int radius,int neighbors){   uchar RITable[256];   int* test;   test = rotation_invariant_mapping(256,8);   for(int i = 0;i < 256;i++)   {     RITable[i] = test[i];   }   Mat result;   result.create(img.rows - 2*radius, img.cols -2*radius , img.type());   result.setTo(0);   for(int i = radius; i   {      for(int j = radius;j    {       uchar center = img.at(i, j);     uchar code = 0;     code |= (img.at(i-radius, j-radius) >= center)<<7;     code |= (img.at(i-radius, j) >= center)<<6;     code |= (img.at(i-radius, j+radius) >= center)<<5;     code |= (img.at(i, j+radius) >= center)<<4;     code |= (img.at(i+radius, j+radius) >= center)<<3;     code |= (img.at(i+radius, j) >= center)<<2;     code |= (img.at(i+radius, j-radius) >= center)<<1;     code |= (img.at(i, j-radius) >= center)<<0;     result.at(i -radius, j -radius) = RITable[code];         }   }   return result;}int main(int argc,char **argv){  Mat src,temp;  src = imread("E:\\lena.bmp",0);   namedWindow("原图",0);  imshow("原图",src);  Mat oriDst = Mat(Size(src.size()), CV_8UC1);  originLBP(src, oriDst);  Mat circularDst = Mat(Size(src.size()),CV_8UC1);  circularDst = circularLBP(src,3,8);  Mat origin_dst_abs;  convertScaleAbs(circularDst,origin_dst_abs);  Mat UniformDst = Mat(Size(src.size()),CV_8UC1);  UniformDst = uniformPatternLBP(src,3,8);  Mat uniform_dst_abs;  convertScaleAbs(UniformDst,uniform_dst_abs);  Mat rotationInvariantDst = Mat(Size(src.size()),CV_8UC1);  rotationInvariantDst = rotationInvariantOfMapLBP(src,3,8);  Mat rotationInvariant_dst_abs;  convertScaleAbs(rotationInvariantDst,rotationInvariant_dst_abs);  namedWindow("oriDst", 0);  imshow("oriDst", oriDst);  namedWindow("circularDst",0);  imshow("circularDst",origin_dst_abs);  namedWindow("UniformDst",0);  imshow("UniformDst",uniform_dst_abs);  namedWindow("rotationInvariantDst",0);  imshow("rotationInvariantDst",rotationInvariant_dst_abs);  waitKey(0);}

下面是运行结果图。 

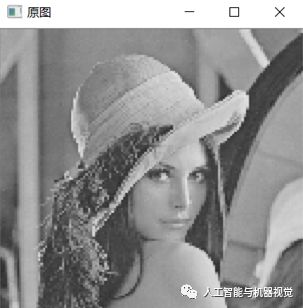
                  图4 原图 

               图5 原始LBP编码

            图6 圆形LBP编码

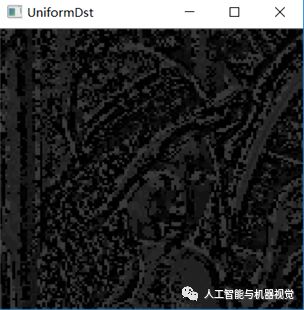
            图7 均衡模式LBP编码

             图8 旋转不变LBP编码