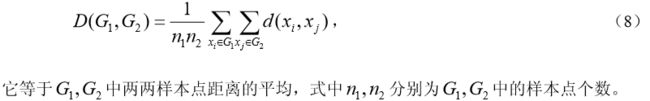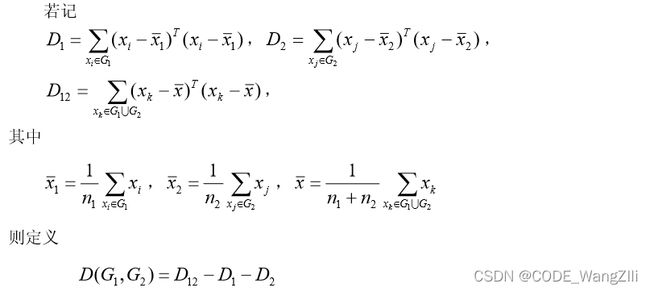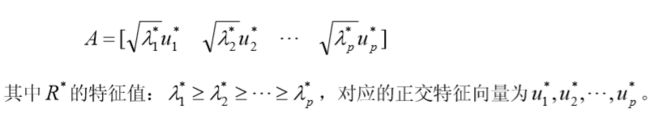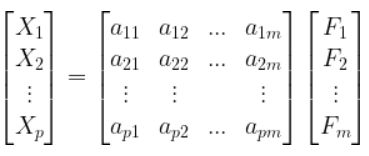数学建模|多元分析(一)
多元分析是多变量的统计分析方法。
聚类分析
聚类分析一般分为Q型聚类分析和R型聚类分析。
- Q型聚类分析是指对样品进行聚类分析
- R型聚类分析是指对变量进行聚类。
根据处理方法的不同聚类分析又分为系统聚类法、有序样品聚类法、动态聚类法、模糊聚类法、图论聚类法。
聚类的一般过程:
- 数据预处理(标准化)
- 构造关系矩阵(亲疏关系的描述)
- 聚类(根据不同方法进行分类)
- 确定最佳分类(类别数)
Q型聚类分析
样本相似性度量
要用数量化的方法对事物进行分类,就必须用数量化的方法描述事物之间的相似程度。一个事物常常需要用多个变量来刻画。如果对于一群有待分类的样本点需用 p p p个变量描述,则每个样本点可以看成是 R p \large R^{p} Rp 空间中的一个点。因此,很自然地想到可以用 距离来度量样本点间的相似程度。
记 Ω \Omega Ω是样本点集,距离 d d d是 Ω × Ω → R + \Omega \times \Omega \rightarrow R^+ Ω×Ω→R+的一个函数,满足条件:
( 1 ) d ( x , y ) ≥ 0 , x , y ∈ Ω (1) d(x,y)\geq0,x,y\in\Omega\\ (1)d(x,y)≥0,x,y∈Ω
( 2 ) d ( x , y ) = 0 当 且 仅 当 x = y (2) d(x,y)=0当且仅当x=y (2)d(x,y)=0当且仅当x=y
( 3 ) d ( x , y ) = d ( y , x ) , x , y ∈ Ω (3) d(x,y)=d(y,x),x,y\in\Omega (3)d(x,y)=d(y,x),x,y∈Ω
( 4 ) d ( x , y ) ≤ d ( x , z ) + d ( z , y ) , x , y , z ∈ Ω (4) d(x,y)\leq d(x,z)+d(z,y),x,y,z\in\Omega (4)d(x,y)≤d(x,z)+d(z,y),x,y,z∈Ω
这一距离的定义是我们所熟知的,它满足正定性,对称性和三角不等式。
在聚类分析中,对于定量变量,常用的闵氏(Minkowski)距离、绝对值距离、欧氏距离、切比雪夫距离。
闵氏距离
d q ( x , y ) = [ ∑ k = 1 p ∣ x k − y k ∣ q ] 1 q , q > 0 d_q(x,y)=[\sum_{k=1}^p|x_k-y_k|^q]^{\frac{1}{q}},q>0 dq(x,y)=[k=1∑p∣xk−yk∣q]q1,q>0
在 Minkowski 距离中,常用的是欧氏距离,它的主要优点是当坐标轴进行正交旋转时,欧氏距离是保持不变的。因此,如果对原坐标系进行平移和旋转变换,则变换 后样本点间的距离和变换前完全相同。
值得注意的是在采用 Minkowski距离时,一定要采用相同量纲的变量。如果变量的量纲不同,测量值变异范围相差悬殊时,建议首先进行数据的标准化处理,然后再计算距离。在采用 Minkowski 距离时,还应尽可能地避免变量的多重相关性(multicollinearity)。多重相关性所造成的信息重叠,会片面强调某些变量的重要性。 由于 Minkowski 距离的这些缺点,一种改进的距离就是马氏距离,定义如下:
马氏距离
d ( x , y ) = ( x − y ) T Σ − 1 ( x − y ) d(x,y)=\sqrt{(x-y)^T\Sigma^{-1}(x-y)} d(x,y)=(x−y)TΣ−1(x−y)
其中 x , y x,y x,y为来自 p p p维总体 Z Z Z的样本观测值; Σ \Sigma Σ为 Z Z Z的协方差矩阵,实际中 Σ \Sigma Σ往往是不知道的,常常需要用样本协方差来估计。马氏距离对一切线性变换是不变的,故不受量纲的影响。
类与类间的相似性度量
如果有两个样本类 G 1 G_1 G1和 G 2 G_2 G2,可以用下面的一系列方法度量它们间的距离:
(1)最短距离法
(2)最长距离法
(3)重心法
(4)类平均法
(5)离差平方和法
事实上,若 G 1 , G 2 G_1,G_2 G1,G2内部点与点距离很小,则它们能很好地各自聚为一类,并且这两类又能够充分分离(即 D 12 D_{12} D12很大),这时必然有 D = D 12 − D 1 − D 2 D=D_{12}-D_1-D_2 D=D12−D1−D2很大。因此,按定义可以认为,两类 G 1 , G 2 G_1,G_2 G1,G2之间的距离很大。离差平方和法初是由 Ward 在 1936 年提出,后经 Orloci 等人 1976 年发展起来的,故又称为 Ward 方法。
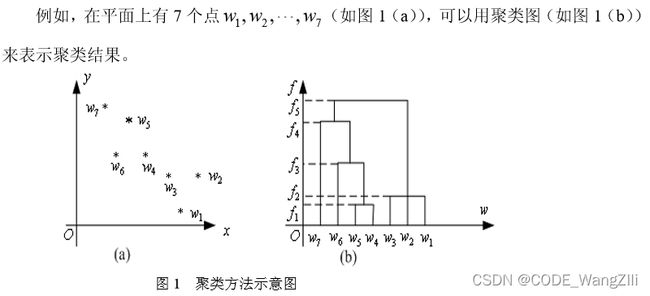
聚类图
Q型聚类结果可由一个聚类图展示出来:
生成聚类图
案例
Q型聚类例子参考博客:
matlab Q型聚类分析例题
Q型聚类分析
R型聚类
变量相似性度量
对变量进行聚类分析,首先要确定变量的相似性度量,常用的变量相似性度量有两张:
相关系数
对变量进行聚类分析的时候,利用相关系数矩阵是最多的。
夹角余弦
各种定义的相似度量均应具有以下两个性质:
变量聚类法
类似样本集合聚类分析中最常用的最短距离法、最长距离法,变量聚类法采用了与系统聚类法相同的思路和过程。在变量聚类问题中,常用的有最长距离法、最短距离法。
最长距离法
在最长距离法中,定义两类变量的距离为:
R ( G 1 , G 2 ) = m a x x j ∈ G 1 , x k ∈ G 2 ∣ d j k ∣ R(G_1,G_2)=max_{x_j\in G_1,x_k\in G_2}|d_{jk}| R(G1,G2)=maxxj∈G1,xk∈G2∣djk∣
式子中: d j k = 1 − ∣ r j k ∣ d_{jk}=1-|r_{jk}| djk=1−∣rjk∣或者 d j k 2 = 1 − r j k 2 d_{jk}^2=1-r_{jk}^2 djk2=1−rjk2,这时, R ( G 1 , G 2 ) R(G_1,G_2) R(G1,G2)与两类中相似性最小的两变量间的相似性度量值有关。
最短距离法
在最短距离法中,定义两类变量的距离为:
R ( G 1 , G 2 ) = m i n x j ∈ G 1 , x k ∈ G 2 ∣ d j k ∣ R(G_1,G_2)=min_{x_j\in G_1,x_k\in G_2}|d_{jk}| R(G1,G2)=minxj∈G1,xk∈G2∣djk∣
式子中: d j k = 1 − ∣ r j k ∣ d_{jk}=1-|r_{jk}| djk=1−∣rjk∣或者 d j k 2 = 1 − r j k 2 d_{jk}^2=1-r_{jk}^2 djk2=1−rjk2,这时, R ( G 1 , G 2 ) R(G_1,G_2) R(G1,G2)与两类中相似性最大的两变量间的相似性度量值有关。
案例
R型聚类分析
聚类算法分类:
主成分分析(PCA)
主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变异,将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。从数学的角度来说,是一种降维处理技术,降维可以去除噪声和不重要的特征,可以提升数据处理的速度。
基本思想
如果用 x 1 , x 2 , ⋅ ⋅ ⋅ , x p x_1,x_2,···,x_p x1,x2,⋅⋅⋅,xp表示 p p p门课程, c 1 , c 2 , ⋅ ⋅ ⋅ , c p c_1,c_2,···,c_p c1,c2,⋅⋅⋅,cp表示各门课程的权重,那么加权之和是:
s = c 1 x 1 + c 2 x 2 + ⋅ ⋅ ⋅ + c p x p s=c_1x_1+c_2x_2+···+c_px_p s=c1x1+c2x2+⋅⋅⋅+cpxp
我们希望选择合适的权重能更好的区分学生的成绩。每个学生都对应一个综合成绩,记为 s 1 , s 2 , ⋅ ⋅ ⋅ , s n , n s_1,s_2,···,s_n,n s1,s2,⋅⋅⋅,sn,n为学生人数,如果这些值很分散,则表明区分的很好,但是现实情况往往是不能很好的分散,所以需要找到一个加权方式来使得 s 1 , s 2 , ⋅ ⋅ ⋅ , s n s_1,s_2,···,s_n s1,s2,⋅⋅⋅,sn尽可能的分散。
有如下的统计定义:
设 X 1 , X 2 , ⋅ ⋅ ⋅ , X p X_1,X_2,···,X_p X1,X2,⋅⋅⋅,Xp表示以 x 1 , x 2 , ⋅ ⋅ ⋅ , x p x_1,x_2,···,x_p x1,x2,⋅⋅⋅,xp为样本观测值的随机变量,如果能找到一组 c 1 , c 2 , ⋅ ⋅ ⋅ , c p c_1,c_2,···,c_p c1,c2,⋅⋅⋅,cp权重3,使得
V a r ( c 1 X 1 + c 2 X 2 + ⋅ ⋅ ⋅ + c p X p ) Var(c_1X_1+c_2X_2+···+c_pX_p) Var(c1X1+c2X2+⋅⋅⋅+cpXp)
的值达到最大,则由于方差反应了数据差异的程度,也就表明了我们抓住了 p p p个变量的最大变异。当然,该式子也必须加上某种限制,不然权值无限大就没有意义了,一般来说规定
c 1 2 + c 2 2 + ⋅ ⋅ ⋅ + c p 2 = 1 c_1^2+c_2^2+···+c_p^2=1 c12+c22+⋅⋅⋅+cp2=1
在此约束条件下,求得的最优解是 p p p纬空间的一个单位向量,它所表示的方向,就是主成分的方向。
实际运用中,一个主成分往往不能代表原来的 p p p变量,所以我们需要寻找第二个、第三个……,且新寻找的主成分不再包含旧主成分的信息。
设 Z i Z_i Zi表示第 i i i个成分, i = 1 , 2 , ⋅ ⋅ ⋅ , p i=1,2,···,p i=1,2,⋅⋅⋅,p,则可以表示为:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \left\{ \begi…
且对每个 i i i,均有 c i 1 2 + c i 2 2 + ⋅ ⋅ ⋅ + c i p 2 = 1 c_{i1}^2+c_{i2}^2+···+c_{ip}^2=1 ci12+ci22+⋅⋅⋅+cip2=1
基本方法
假设有n个样本,p个指标,则可以构成大小为 n × p n\times p n×p的矩阵 x x x
x = [ x 11 x 12 ⋅ ⋅ ⋅ x 1 p x 21 x 22 ⋅ ⋅ ⋅ x 2 p ⋅ ⋅ ⋅ x n 1 x n 2 ⋅ ⋅ ⋅ x n p ] = ( x 1 , x 2 , ⋅ ⋅ ⋅ , x p ) x={\left[ {\begin{matrix} x_{11}&x_{12}&···&x_{1p}\\ x_{21}&x_{22}&···&x_{2p}\\···\\ x_{n1}&x_{n2}&···&x_{np}\\ \end{matrix}} \right]=(x_1,x_2,···,x_p)} x=⎣⎢⎢⎡x11x21⋅⋅⋅xn1x12x22xn2⋅⋅⋅⋅⋅⋅⋅⋅⋅x1px2pxnp⎦⎥⎥⎤=(x1,x2,⋅⋅⋅,xp)
1. 进行标准化处理
按列计算均值 x j ˉ = 1 n ∑ i = 1 n x i j \bar{x_j}=\frac{1}{n}\sum_{i=1}^nx_{ij} xjˉ=n1∑i=1nxij和标准差
S j = ∑ i = 1 n ( x i j − x j ˉ ) n − 1 S_j=\sqrt{\frac{\sum_{i=1}^n(x_{ij}-\bar{x_j})}{n-1}} Sj=n−1∑i=1n(xij−xjˉ)
再标准化数据 X i j = x i j − x j ˉ S j X_{ij}=\frac{x_{ij}-\bar{x_j}}{S_j} Xij=Sjxij−xjˉ,原始样本矩阵经过标准化为:
X = [ X 11 X 12 ⋅ ⋅ ⋅ X 1 p X 21 X 22 ⋅ ⋅ ⋅ X 2 p ⋅ ⋅ ⋅ X n 1 X n 2 ⋅ ⋅ ⋅ X n p ] = ( X 1 , X 2 , ⋅ ⋅ ⋅ , X p ) X={\left[ {\begin{matrix} X_{11}&X_{12}&···&X_{1p}\\ X_{21}&X_{22}&···&X_{2p}\\···\\ X_{n1}&X_{n2}&···&X_{np}\\ \end{matrix}} \right]=(X_1,X_2,···,X_p)} X=⎣⎢⎢⎡X11X21⋅⋅⋅Xn1X12X22Xn2⋅⋅⋅⋅⋅⋅⋅⋅⋅X1pX2pXnp⎦⎥⎥⎤=(X1,X2,⋅⋅⋅,Xp)
2. 计算标准化样本的协方差矩阵
R = [ r 11 r 12 ⋅ ⋅ ⋅ r 1 p r 21 r 22 ⋅ ⋅ ⋅ r 2 p ⋅ ⋅ ⋅ r n 1 r n 2 ⋅ ⋅ ⋅ r n p ] R={\left[ {\begin{matrix} r_{11}&r_{12}&···&r_{1p}\\ r_{21}&r_{22}&···&r_{2p}\\···\\ r_{n1}&r_{n2}&···&r_{np}\\ \end{matrix}} \right]} R=⎣⎢⎢⎡r11r21⋅⋅⋅rn1r12r22rn2⋅⋅⋅⋅⋅⋅⋅⋅⋅r1pr2prnp⎦⎥⎥⎤
其中
r i j = 1 n − 1 ∑ k = 1 n ( X k i − X i ˉ ) ( X k j − X j ˉ ) = 1 n − 1 ∑ k = 1 n X k i X k j r_{ij}=\frac{1}{n-1}\sum_{k=1}^n(X_{ki}-\bar{X_i})(X_{kj}-\bar{X_j})=\frac{1}{n-1}\sum_{k=1}^nX_{ki}X_{kj} rij=n−11k=1∑n(Xki−Xiˉ)(Xkj−Xjˉ)=n−11k=1∑nXkiXkj
其实这两步可以合成一步,
R = ∑ k = 1 n ( x k i − x i ˉ ) ( x k j − x j ˉ ) ∑ k = 1 n ( x k i − x i ˉ ) 2 ∑ k = 1 n ( x k j − x j ˉ ) 2 R=\frac{\sum_{k=1}^n(x_{ki}-\bar{x_i})(x_{kj}-\bar{x_j})}{\sqrt{\sum_{k=1}^n(x_{ki}-\bar{x_i})^2\sum_{k=1}^n(x_{kj}-\bar{x_j})^2}} R=∑k=1n(xki−xiˉ)2∑k=1n(xkj−xjˉ)2∑k=1n(xki−xiˉ)(xkj−xjˉ)
3. 计算 R R R的特征值和特征向量
特征值:
λ 1 ≥ λ 2 ≥ ⋅ ⋅ ⋅ ≥ λ p ≥ 0 \lambda_1\geq\lambda_2\geq···\geq\lambda_p\geq 0 λ1≥λ2≥⋅⋅⋅≥λp≥0( R R R是半定矩阵,且 t r ( R ) = ∑ k = 1 p λ k = p tr(R)=\sum_{k=1}^p\lambda_k=p tr(R)=∑k=1pλk=p)
特征向量:
a 1 = [ a 11 a 21 ⋅ ⋅ ⋅ a p 1 ] , a 2 = [ a 12 a 22 ⋅ ⋅ ⋅ a p 2 ] , ⋅ ⋅ ⋅ , a p = [ a 1 p a 2 p ⋅ ⋅ ⋅ a p p ] a_1={\left[ {\begin{matrix} a_{11}\\ a_{21}\\···\\ a_{p1} \end{matrix}} \right],a_2={\left[ {\begin{matrix} a_{12}\\ a_{22}\\···\\ a_{p2} \end{matrix}} \right],···,a_p={\left[ {\begin{matrix} a_{1p}\\ a_{2p}\\···\\ a_{pp} \end{matrix}} \right]}}} a1=⎣⎢⎢⎡a11a21⋅⋅⋅ap1⎦⎥⎥⎤,a2=⎣⎢⎢⎡a12a22⋅⋅⋅ap2⎦⎥⎥⎤,⋅⋅⋅,ap=⎣⎢⎢⎡a1pa2p⋅⋅⋅app⎦⎥⎥⎤
Matlab中计算特征值和特征向量的函数: e i g ( R ) eig(R) eig(R)
4. 计算主成分贡献率以及累计贡献率
贡献率:
λ i ∑ k = 1 p , ( i = 1 , 2 , ⋅ ⋅ ⋅ , p ) \frac{\lambda_i}{\sum_{k=1}^p},(i=1,2,···,p) ∑k=1pλi,(i=1,2,⋅⋅⋅,p)
累计贡献率:
∑ k = 1 i λ k ∑ k = 1 p λ k , ( i = 1 , 2 , ⋅ ⋅ ⋅ , p ) \frac{\sum_{k=1}^i\lambda_k}{\sum_{k=1}^p\lambda_k},(i=1,2,···,p) ∑k=1pλk∑k=1iλk,(i=1,2,⋅⋅⋅,p)
5.写出主成分
一般取累计贡献率超过 80 % 80\% 80%的特征值所对应的第一、第二、……、第m ( m ≤ p ) (m\leq p) (m≤p)个主成分,第 i i i个主成分:
F i = a 1 i X 1 + a 2 i X 2 + ⋅ ⋅ ⋅ + a p i X p , ( i = 1 , 2 , ⋅ ⋅ ⋅ , m ) F_i=a_{1i}X_1+a_{2i}X_2+···+a_{pi}X_p,(i=1,2,···,m) Fi=a1iX1+a2iX2+⋅⋅⋅+apiXp,(i=1,2,⋅⋅⋅,m)
6. 根据系数分析主成分代表的意义
简而言之,系数越大,影响越大
主成分分析回归
主成分可用于聚类分析、回归分析。不可用于评价类模型!
例如Hald水泥问题,参考这里:水泥问题及matlab代码在文章尾部
案例
数学建模常用模型08 :主成分分析
数学建模–主成分分析
数学建模算法 一 简述(4)主成分分析(PCA)
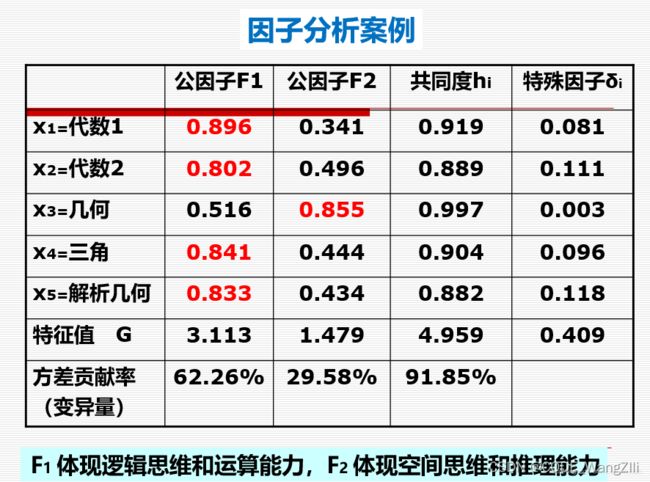
因子分析(FA)
因子分析可以看做是主成分分析的推广,也是利用降维的思想,由研究原始变量相关矩阵或协方差矩阵的内部依赖关系出发,把一些具有错综复杂关系的多个变量归 结为少数几个综合因子的一种多元统计分析方法。
基本思想
把每个研究变量分解为几个影响因素变量,将每个原始变量分解成两部分因素,一部分是由所有变量共同具有的少数几个公共因子组成的,另一部分是每个变量独自具有的因素,即特殊因子。
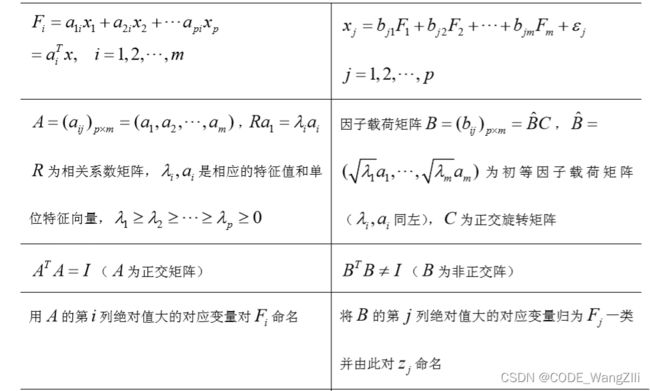
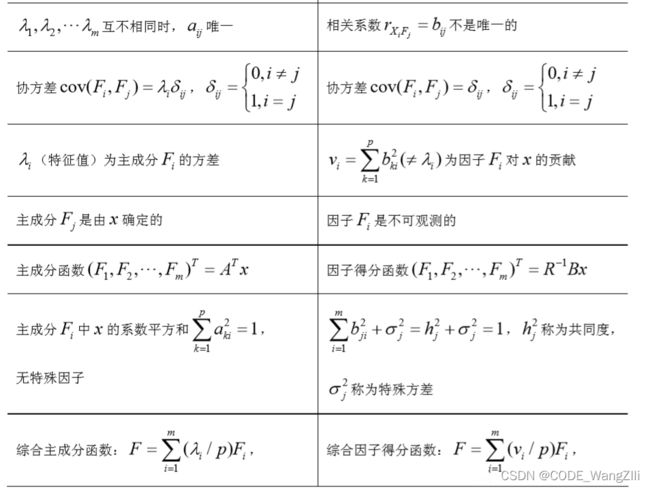
与主成分分析的区别
- 主成分分析模型是原始变量的线性组合,是将原始变量加以综合、归纳,仅仅是变量变换;而因子分析是将原始变量加以分解,描述原始变量协方差矩阵结构的模型;只有当提取的公因子个数等于原始变量个数时,因子分析才对应变量变换。
- 主成分分析中每个主成分对应的系数是唯一确定的;因子分析中每个因子的相应系数即因子载荷不是唯一的。
- 因子分析中因子载荷的不唯一性有利于对公因子进行有效解释; 而主成分分析对提取的主成分的解释能力有限。
因子分析模型
因子载荷矩阵中的几个统计性质
-
因子载荷 α i j \alpha_{ij} αij的统计意义
因子载荷 α i j \alpha_{ij} αij是第 i i i个变量与 j j j个公共因子的相关系数,反映了第 i i i个变量与第 j j j个公共因子的相关重要性,绝对值越大,相关的密切程度越高。 -
变量共同度的统计意义
变量 X i X_i Xi的共同度是因子载荷矩阵的第 i i i行的元素的平方和,记为 h i 2 = ∑ j = 1 m a i j 2 h_i^2=\sum_{j=1}^ma_{ij}^2 hi2=∑j=1maij2,对两边求方差,有V a r ( X i ) = α i 1 2 V a r ( F 1 ) + ⋅ ⋅ ⋅ + α i m 2 V a r ( F m ) + V a r ( ε i ) Var(X_i)=\alpha_{i1}^2Var(F_1)+···+\alpha_{im}^2Var(F_m)+Var(\varepsilon_i) Var(Xi)=αi12Var(F1)+⋅⋅⋅+αim2Var(Fm)+Var(εi)
即
1 = ∑ j = 1 m α i j 2 + σ i 2 1=\sum_{j=1}^m\alpha_{ij}^2+\sigma_i^2 1=j=1∑mαij2+σi2
可以看出所有的公共因子对特殊因子对变量 X i X_i Xi的贡献为 1 1 1,如果 h i 2 h_i^2 hi2非常接近 1 1 1,说明从原变量空间到公共因子空间的转化效果好。
-
公共因子 F j F_j Fj方差贡献的统计意义
因子载荷矩阵中各列元素的平方和
S j = ∑ i = 1 p α i j 2 S_j=\sum_{i=1}^p\alpha_{ij}^2 Sj=i=1∑pαij2
则称 F j ( j = 1 , 2 , ⋅ ⋅ ⋅ , m ) F_j(j=1,2,···,m) Fj(j=1,2,⋅⋅⋅,m)对所有的 X i X_i Xi的方差贡献和,用于衡量 F j F_j Fj的相对重要性。
因子载荷矩阵的估计方法
因子分析的一个基本问题是如何估计因子载荷,即如何求解因子模型式,下面介绍常用的因子载荷矩阵的估计方法。
主成分分析法
设 λ 1 ≥ λ 2 ≥ ⋅ ⋅ ⋅ ≥ λ p ≥ λ p \lambda_1\geq\lambda_2\geq···\geq\lambda_p\geq \lambda_p λ1≥λ2≥⋅⋅⋅≥λp≥λp为样本相关系数矩阵 R R R的特征值, η 1 , η 2 , ⋅ ⋅ ⋅ , η p \eta_1,\eta_2,···,\eta_p η1,η2,⋅⋅⋅,ηp为相应的标准正交化特征向量,设 m < p m m<p
实例参考(含matlab代码):因子分析—建立载荷矩阵
主因子法
主因子法是对主成分法的修正,
首先对变量标准化
R = Λ Λ T + D , D = d i a g { σ 1 2 , ⋅ ⋅ ⋅ , σ m 2 } 。 R=\Lambda \Lambda^T+D,D=diag\{\sigma_1^2,···,\sigma_m^2\}。 R=ΛΛT+D,D=diag{σ12,⋅⋅⋅,σm2}。
记
R ∗ = Λ Λ T = R − D R^*=\Lambda\Lambda^T=R-D R∗=ΛΛT=R−D
式中, R ∗ R^* R∗为约相关系数矩阵, R ∗ R^* R∗对角线上的元素是 h i 2 h_i^2 hi2。
在实际情况中对特殊因子的方差一般是未知的,可以通过一组样本来估计,估计的方法如下:
- 取 h i 2 ^ = 1 \hat{h_i^2}=1 hi2^=1,在这种情况下主因子解与主成分解等价
- 取 h i 2 ^ = m a x j ≠ i ∣ r i j ∣ \hat{h_i^2}=max_{j\neq i}|r_{ij}| hi2^=maxj=i∣rij∣,这意味着 X i X_i Xi与其余的 X j X_j Xj的简单相关系数的绝对值最大者。
记作
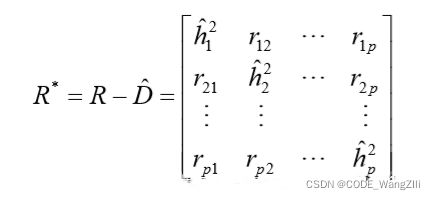
直接求 R ∗ R^* R∗的前 p p p个特征值 λ 1 ∗ ≥ λ 2 ∗ ≥ ⋅ ⋅ ⋅ ≥ λ p ∗ ≥ λ p \lambda_1^*\geq\lambda_2^*\geq···\geq\lambda_p^*\geq \lambda_p λ1∗≥λ2∗≥⋅⋅⋅≥λp∗≥λp和对应的正交特征向量 u 1 ∗ , u 2 ∗ , ⋅ ⋅ u p ∗ u_1^*,u_2^*,··u_p^* u1∗,u2∗,⋅⋅up∗。
得到如下的因子载荷矩阵:
极大似然估计
Matlab工具箱求因子载荷矩阵使用的是最大似然估计法,命令是 f a c t o r a n factoran factoran
案例
数学建模常用模型14 :因子分析
因子旋转(正交变换)
为什么要旋转因子?
建立了因子分析数学目的不仅仅要找出公共因子以及对变量进行分组,更重要的要知道每个公共因子的意义,以便进行进一步的分析,如果每个公共因子的含义不清,则不便于进行实际背景的解释。由于因子载荷阵是不唯一的,所以应该对因子载荷阵进行旋转。目的是使每个变量在尽可能少的因子上有比较高的载荷,让某个变量在某个因子上的载荷趋于1,而在其他因子上的载荷趋于0。
即:使载荷矩阵每列或行的元素平方值向0和1两极分化。
旋转的方法有:正交旋转;斜交旋转
正交旋转
由初始载荷矩阵A左乘一正交矩阵得到;目的是新的载 荷系数尽可能的接近于0或尽可能的远离0;只是在旋 转后的新的公因子仍保持独立性。
- 方差最大法: 方差最大法从简化因子载荷矩阵的每一列出发,使和每个因子有关的载荷的平方的方差最大。当只有少数几个变量在某个因子上有较高的载荷时,对因子的解释最简单。方差最大的直观意义是希望通过因子旋转后,使每个因子上的载荷尽量拉开距离,一部分的载荷趋于 1,另一部分趋于0。
- 四次方最大旋转: 四次方最大旋转是从简化载荷矩阵的行出发,通过旋转 初始因子,使每个变量只在一个因子上有较高的载荷, 而在其它的因子上尽可能低的载荷。如果每个变量只在 一个因子上有非零的载荷,这时的因子解释是最简单的。 四次方最大法通过使因子载荷矩阵中每一行的因子载 荷平方的方差达到最大。
- 等量最大法: 等量最大法把四次方最大法和方差最大法结合起来求行和列因子载荷平方的方差的加权平均最大。
斜交旋转
目的是新的载荷系数尽可能的接近于0或尽可能的远离0;只是在旋转时,放弃了因子之间彼此独立的限制,旋转后的新公因子更容易解释。主要有以下的方法:
- 直接斜交旋转。允许因子之间具有相关性;
- 斜交旋转方法。允许因子之间具有相关性;
具体算法过程参考因子分析法之因子旋转
因子得分
积分因子的概念
前面我们主要解决了用公共因子的线性组合来表示一组观测变量的有关问题。如果我们要使用这些因子做其他的研究,比如把得到的因子作为自变量来做回归分析,对样 本进行分类或评价,这就需要我们对公共因子进行测度,即给出公共因子的值。
因子分析数学模型
原变量被表示为公共因子的线性组合,当载荷矩阵旋转之后,公共因子可以做出解释,通常的情况下,我们还想反过来把公共因子表示为原变量的线性组合。
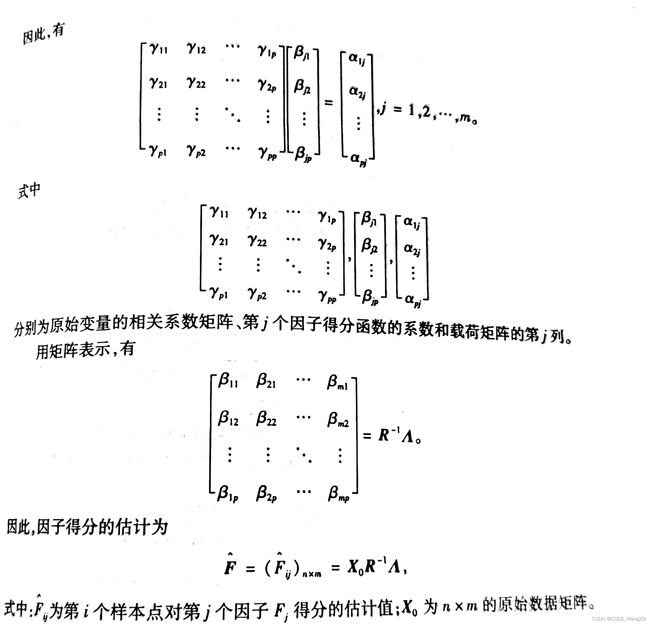
得分因子函数:
可见,要求得每个因子的得分,必须求得分函数的系数,而由于 p > m,所以不能得到精确的得分,只能通过估计。
巴特莱特因子得分(加权最小二乘法)
把 X i − μ i X_i-\mu_i Xi−μi看作因变量,把因子载荷矩阵
还可参考以下博客:
因子分析 factor analysis (五) : 因子得分
因子分析——因子得分
案例
因子分析 factor analysis (六) :用因子分析法进行综合评价
因子分析步骤与主成分分析对比
相同:
- 指标标准化
- 相关系数矩阵及其特征值和特征向量
- 用累计贡献率确定主成分和因子个数m
- 单个主成分与综合主成分的分析评价、单因子与综合因子的分析评价步骤
不同之处:
参考博客
参考博客:
-
多元统计分析 (一):聚类分析
-
数学建模–主成分分析
-
数学建模常用模型14 :因子分析