吴恩达机器学习笔记(自己学的过程进行记录)
吴恩达机器学习笔记(自己学着记)
1. 机器学习分类
1.1 监督学习
1.1.1 回归
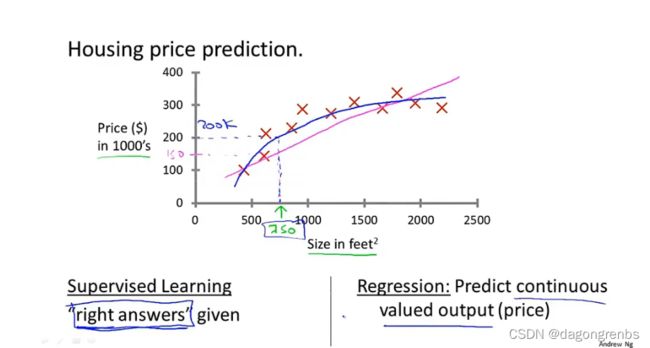
回归问题是在知道正确答案的基础上进行的,即给定的数据集是真实的一系列连续的值。计算机通过学习选择适当的模型来模拟这个数据值(比如一次函数或二次函数等)例:房价随面积的变化
1.1.2 分类
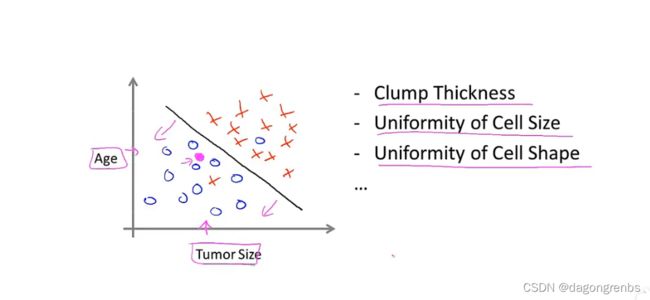
分类问题是离散的值,比如非0即1的情况 下图是乳腺癌的分类问题,要么恶性要么良性,是离散的
多维的分类问题
1.2 无监督学习
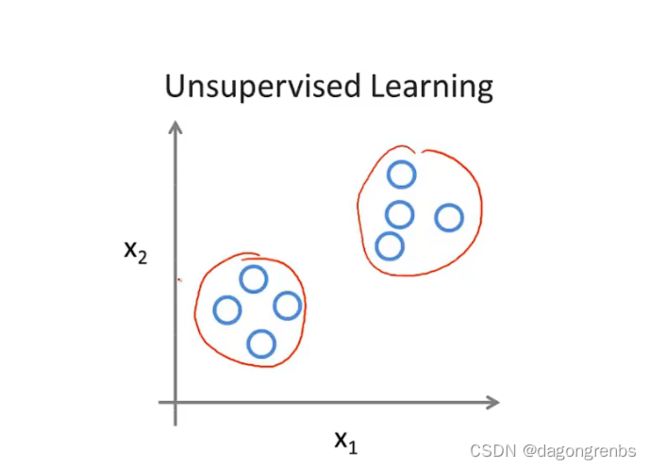
1.2.1 聚类
事先不知道正确答案,也不知道要分成多少类
可以用在新闻的分类上,将类似的新闻放到一个簇中,主要应用场景如下。
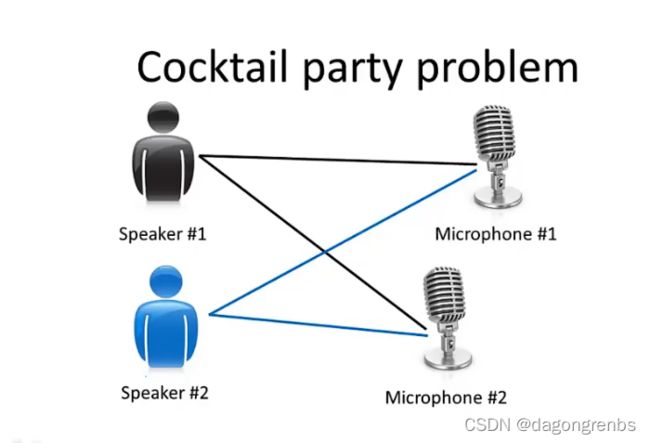
1.2.2 特征提取
鸡尾酒会上从不同的声音提取声音,去除噪声也属于无监督学习
2. 线性回归模型
2.1 模型简介
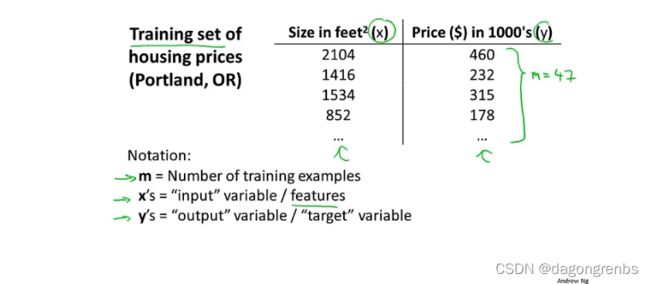
还是以房价和尺寸的关系为例,模型一些常见的符号含义
(x,y)代表一个训练样本, ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i) }) (x(i),y(i))代表第i个训练样本
模型的过程, h称为假设函数。
2.2 代价函数
2.2.1 定义
假设函数中的 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1被称为参数,参数的合理选择可以使我们的结果更好地收敛,或者说能够更好的预测值。
为了更好地预测,我们的目标就是:
m i n i m i z e θ 0 , θ 1 1 2 m ∑ i = 1 m ( h θ ( x ( i ) − y ( i ) ) 2 minimize_{\theta_0,\theta_1}\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)}-y^{(i)})^2 minimizeθ0,θ12m1i=1∑m(hθ(x(i)−y(i))2
因此我们可以得到代价函数为
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
代价函数也被称为平方误差函数,也叫平方误差代价函数
2.2.2 原理及内涵
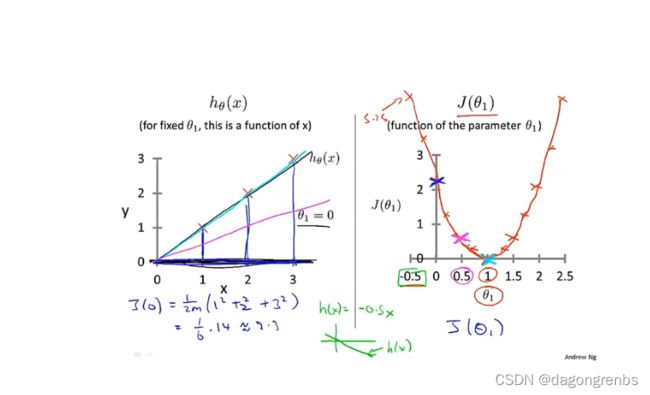
代价函数的直观上的表达,这里以 h θ ( x ) = θ 1 x h_\theta(x)=\theta_1x hθ(x)=θ1x为例
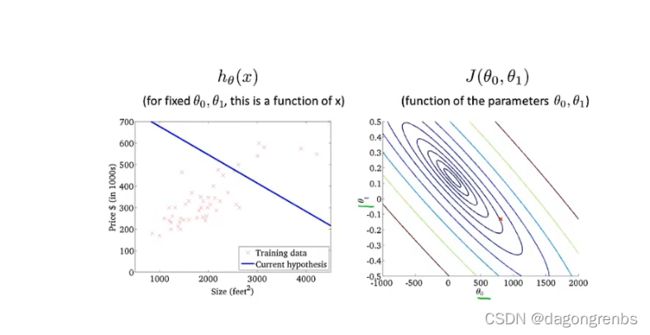
下面进阶成 h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1x hθ(x)=θ0+θ1x的情况,代价函数成了等高线图
2.3 梯度下降
2.3.1 含义
给定初始参数 θ 0 , θ 1 , ⋯ , θ m \theta_0,\theta_1,\cdots,\theta_m θ0,θ1,⋯,θm,通过不断地改变 θ 0 , θ 1 , ⋯ , θ m \theta_0,\theta_1,\cdots,\theta_m θ0,θ1,⋯,θm,使得代价函数不断减少,这就是梯度下降的过程
梯度下降法的公式
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_j:=\theta_j-\alpha\frac{\partial}{\partial \theta_j}J(\theta_0,\theta_1) θj:=θj−α∂θj∂J(θ0,θ1)
梯度下降是同时进行的也就是说:
2.3.2 注意事项
α \alpha α是学习率 ,太大可能会无法收敛,太小可能收敛缓慢,因此选择一个适当的值很重要。具体如下,从图上可以直观地进行理解:
当到达局部最优点之后,由于偏导为0,则不会继续变化
2.3.3 线性回归的梯度下降
上面学到的梯度下降算法被称为“Batch”梯度下降,每一步训练都遍历整个样本。
2.4 多元梯度下降
前面讨论的一元问题,房子的价格仅跟房屋面积有关,现实中应该是跟很多因素有关,下面讨论多元问题的梯度下降
2.4.1 问题描述
注:以 x j ( i ) x_{j}^{(i)} xj(i)为例说明,可以简单地理解为 i i i代表行, j j j代表列 例: x ( 2 ) = [ 1416 , 3 , 2 , 40 ] T , x 3 ( 2 ) = 2 x^{(2)}=[1416,3,2,40]^T, x_{3}^{(2)}=2 x(2)=[1416,3,2,40]T,x3(2)=2
这样多元问题可以表示为:
h θ ( x ) = θ 0 + θ 1 x 1 + ⋯ + θ n x n h_\theta(x)=\theta_0+\theta_1x_1+\cdots+\theta_nx_n hθ(x)=θ0+θ1x1+⋯+θnxn
为了表示方便,取 x 0 = 1 x_0=1 x0=1
2.4.2 多元梯度下降法
2.4.2.1 定义及基本概念
接下来给出一元和多元的梯度下降算法的对比
品红色圈出来的是等效的,because x 0 ( i ) = 1 x_{0}^{(i)}=1 x0(i)=1
2.4.2.2 特征缩放
还是以房屋价格为例,面积尺寸假设为0-200平方米,而楼层可能只有1-5层,这时候需要进行特征缩放。原因是当不同特征差距过大时,等高线图可能会过于扁平或过于细窄
缩放方法
使用 x 1 − μ 1 s 1 \frac{x_1-\mu_1}{s_1} s1x1−μ1来代替 x 1 x_1 x1,其中 μ 1 \mu_1 μ1为训练集中特征 x 1 x_1 x1的平均值, s 1 = m a x ( x 1 ) − m i n ( x 1 ) s_1=max(x_1)-min(x_1) s1=max(x1)−min(x1),也就是范围
2.4.2.3 学习率的选取
1.采用自动收敛计算,给一个阈值,当真实值与预测值的差值小于该阈值,即可认为收敛
2.画出图像,直观可视化
选择学习率的时候以三倍进行比较好0.001,0.003,0.01,0.03,…。
2.4.3 特征和多项式回归
以预测房价为例,房屋价格与面积,体积等有关系,可以列为 h θ ( x ) = θ 0 + θ 1 ( s i z e ) + θ 2 ( s i z e ) 2 + θ 3 ( s i z e ) 3 h_\theta(x)=\theta_0+\theta_1(size)+\theta_2(size)^2+\theta_3(size)^3 hθ(x)=θ0+θ1(size)+θ2(size)2+θ3(size)3
将多次方转化为一次方线性回归:令 x 1 = ( s i z e ) , x 2 = ( s i z e ) 2 , x 3 = ( s i z e ) 3 x_1=(size),x_2=(size)^2,x_3=(size)^3 x1=(size),x2=(size)2,x3=(size)3
则原式化为 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3 hθ(x)=θ0+θ1x1+θ2x2+θ3x3
房价预测,一个常见的修改假设函数使得更能模拟真实情况的,就是将平方项改为开根号,因为平方项最后肯定会下降,而房价随着尺寸的增大是不会下降的
2.5 正规方程
正规方程是一种区别于迭代方法的直接解法
式子: θ = ( X T X ) ( − 1 ) X T y \theta=(X^TX)^{(-1)}X^Ty θ=(XTX)(−1)XTy
正规方程法与梯度下降法的优缺点:
- 正规方程不需要选择学习率也不需要迭代
- 但是当n变大之后,正规方程的计算不方便
如果不可逆怎么解决?