PyTorch学习-线性模型

将数据分为训练集、验证集(x,y)和测试集(x)。注意过拟合，提高模型的泛化能力。
线性模型(Linear Model)：$y^{\prime }=x\ast w+b$，$x,w,b$ 往往是矩阵
目的就是求$w,b$的值
假设 $loss=(y^{\prime }-y{)}^2=(x\ast w-y{)}^2$
要使 $loss$的值最小
平均平方误差(Mean Square Error, MSE) : $cost=\frac{1}{N}\sum (y_n^{\prime }-y_n{)}^2$

$y=x\ast w$ 的情况

需要的包：

import numpy as np	# 矩阵操作
import matplotlib.pyplot as plt	# 画图

需要拟合的数据：

x_data = [1.0, 2.0,3.0]
y_data = [2.0, 4.0,6.0]

定义损失函数

def forward(x):  # 线性模型：y = x*w
    return x * w

def loss(x, y):  # 损失函数定义
    y_pred = forward(x)
    return (y_pred - y)*(y_pred - y)

枚举线性模型的权值w，计算损失函数的值

w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1): # 形成一个[0, 4.1) 间隔0.1的排列代表w的值，暴力枚举
    print("w = ", w)   # 取出一个假设的权重
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred = forward(x_val)    # y的预测值
        loss_val = loss(x_val, y_val)    # 损失值
        l_sum += loss_val
        print("\t", x_val, y_val, y_pred, loss_val)
    print("MSE = ", l_sum / 3)
    w_list.append(w)    # 加入到权重列表
    mse_list.append(l_sum / 3)   # 加入到MSE的列表里

输出结果：

w =  0.0
	 1.0 2.0 0.0 4.0
	 2.0 4.0 0.0 16.0
	 3.0 6.0 0.0 36.0
MSE =  18.666666666666668
w =  0.1
	 1.0 2.0 0.1 3.61
	 2.0 4.0 0.2 14.44
	 3.0 6.0 0.30000000000000004 32.49
MSE =  16.846666666666668
w =  0.2
	 1.0 2.0 0.2 3.24
	 2.0 4.0 0.4 12.96
	 3.0 6.0 0.6000000000000001 29.160000000000004
MSE =  15.120000000000003
w =  0.30000000000000004
	 1.0 2.0 0.30000000000000004 2.8899999999999997
	 2.0 4.0 0.6000000000000001 11.559999999999999
	 3.0 6.0 0.9000000000000001 26.009999999999998
MSE =  13.486666666666665
w =  0.4
	 1.0 2.0 0.4 2.5600000000000005
	 2.0 4.0 0.8 10.240000000000002
	 3.0 6.0 1.2000000000000002 23.04
MSE =  11.946666666666667
w =  0.5
	 1.0 2.0 0.5 2.25
	 2.0 4.0 1.0 9.0
	 3.0 6.0 1.5 20.25
MSE =  10.5
w =  0.6000000000000001
	 1.0 2.0 0.6000000000000001 1.9599999999999997
	 2.0 4.0 1.2000000000000002 7.839999999999999
	 3.0 6.0 1.8000000000000003 17.639999999999993
MSE =  9.146666666666663

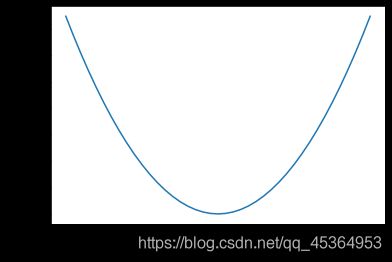
画出权值w和损失函数的图像，w为自变量，mes(loss)为因变量，观察变化趋势

plt.plot(w_list, mse_list)
plt.ylabel("Loss")
plt.xlabel("w")
plt.show()

画出的图像：
观察可以看见w=0的时候loss最低为0，对应拟合函数y=2x，非常符合训练数据

$y=x\ast w+b$ 的情况

import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0,3.0]
y_data = [2.0, 4.0,6.0]
def forward(x):  # 线性模型：y = x*w
    return x * w + b

def loss(x, y):  # 损失函数定义
    y_pred = forward(x)
    return (y_pred - y)*(y_pred - y)

w_list = []
b_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1): # 形成一个[0, 4.1) 间隔0.1的排列代表w的值，暴力枚举
    for b in np.arange(-2.0, 2.0, 0.1): 
        print("w = ", w,"b = ",b)   # 取出一个假设的权重
        l_sum = 0
        for x_val, y_val in zip(x_data, y_data):
            y_pred = forward(x_val)    # y的预测值
            loss_val = loss(x_val, y_val)    # 损失值
            l_sum += loss_val
            print("\t", x_val, y_val, y_pred, loss_val)
        print("MSE = ", l_sum / 3)
        w_list.append(w)    # 加入到权重列表
        mse_list.append(l_sum / 3)   # 加入到MSE的列表里
        b_list.append(b)

输出：

w =  0.0 b =  -2.0
	 1.0 2.0 -2.0 16.0
	 2.0 4.0 -2.0 36.0
	 3.0 6.0 -2.0 64.0
MSE =  38.666666666666664
w =  0.0 b =  -1.9
	 1.0 2.0 -1.9 15.209999999999999
	 2.0 4.0 -1.9 34.81
	 3.0 6.0 -1.9 62.410000000000004
MSE =  37.47666666666667
w =  0.0 b =  -1.7999999999999998
	 1.0 2.0 -1.7999999999999998 14.44
	 2.0 4.0 -1.7999999999999998 33.64
	 3.0 6.0 -1.7999999999999998 60.839999999999996
MSE =  36.306666666666665
w =  0.0 b =  -1.6999999999999997
	 1.0 2.0 -1.6999999999999997 13.689999999999998
	 2.0 4.0 -1.6999999999999997 32.489999999999995
	 3.0 6.0 -1.6999999999999997 59.28999999999999
MSE =  35.15666666666666
w =  0.0 b =  -1.5999999999999996
	 1.0 2.0 -1.5999999999999996 12.959999999999997
	 2.0 4.0 -1.5999999999999996 31.359999999999996
	 3.0 6.0 -1.5999999999999996 57.76
MSE =  34.026666666666664
w =  0.0 b =  -1.4999999999999996
	 1.0 2.0 -1.4999999999999996 12.249999999999996
	 2.0 4.0 -1.4999999999999996 30.25
	 3.0 6.0 -1.4999999999999996 56.25
MSE =  32.916666666666664
w =  0.0 b =  -1.3999999999999995
	 1.0 2.0 -1.3999999999999995 11.559999999999997
	 2.0 4.0 -1.3999999999999995 29.159999999999993
	 3.0 6.0 -1.3999999999999995 54.75999999999999
MSE =  31.826666666666664
w =  0.0 b =  -1.2999999999999994
	 1.0 2.0 -1.2999999999999994 10.889999999999995
	 2.0 4.0 -1.2999999999999994 28.08999999999999
	 3.0 6.0 -1.2999999999999994 53.289999999999985
MSE =  30.756666666666657
... ...

画图：

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot3D(w_list,b_list, mse_list)
plt.show()

画图结果：

想用plot_surface函数画图来着，但是遇到了各种各样的报错，最终放弃了，下面是该函数的画图结果：