数字信号处理实验：信号谱分析与FFT算法的应用

一. 实验目的

1． 观察模拟信号经理想采样后的频谱变化关系。

2． 验证采样定理，观察欠采样时产生的频谱混叠现象

3． 加深对DFT算法原理和基本性质的理解

4． 熟悉FFT算法原理和FFT的应用

二. 实验原理

    1.时域抽样定理：为了能从抽样信号中恢复原信号x(t)，需要满足连个条件：x(t)必须为带限信号；抽样频率不能太低，必须满足 ，或者说抽样间隔不能太大，必须满足 ，否则将会发生混叠。通常把最低允许抽样频率 称为奈奎斯特频率，把最大允许抽样间隔 称为奈奎斯特间隔。

    2.利用DFT对连续信号进行频谱分析：先对连续信号进行傅里叶变换，分析其频谱，然后进行时域抽样，得到离散信号。再对离散信号进行DFT，得到在频域区间０~２π 上的N点等间隔抽样。

    ３.线性卷积： 。计算步骤为：变量代换、反褶、移位、相乘和累加，最后便得出结果。

    ４.圆周卷积：周期卷积和圆周卷积具有类似的形式，但是求和区间和线性卷积不同。周期卷积中而者乘积也是周期为N的序列。且周期卷积满足交换律。

三. 实验内容

       （1）给定信号为 ，其中ａ为42，ｂ为1。理论分析信号 的频率成分。

     （2）分别采用采样频率为 ， ， ， 对 进行采样，其中 ， ， ， ，根据是否满足采样定理要求分析四种采样频率下频谱的分布，在满足采样定理情况下做频谱分析。

      （3）任意生成两组有限长信号，对信号分别进行直接卷积和FFT算法求卷积，并分析圆周卷积与线性卷积的关系。

四. 实验步骤

        ①给定信号 ，其中ａ为42，ｂ为1。理论分析信号 的频率成分。

        实验代码：

clc,clear;
a=42;b=1;
fs=20000;   %采样频率
f1=a*b*50;f2=a*b*100;f3=a*b*150;  %待滤波余弦信号频率
t=(0:400)/fs;   %定义时间步长
s=4*cos(2*f1*pi*t)+2*cos(2*f2*pi*t)+cos(2*f3*pi*t);
subplot(211);plot(t,s);  %滤波前的信号图像
axis([0 0.005 -3.5 7.5]);
xlabel('时间/秒');ylabel('幅度');title('信号滤波前时域图');
Fs=fft(s,512);AFs=abs(Fs);f=fs/512*(0:255);
subplot(212);plot(f,AFs(1:256));     %滤波前的信号频谱图
xlabel('频率/赫兹');ylabel('幅度');title('信号滤波前频域图');

        仿真结果：

 

由于 是由三个余弦分量组成的周期信号，所以对每一个信号进行分析可得： 的频率分量分别为 。有图1可知： 信号是周期信号，其三个频域分量为2100Hz、4200Hz和6300Hz，满足上述分析结果。

    ②分别采用采样频率为 ， ， ， 对 进行采样，其中 ， ， ， ，根据是否满足采样定理要求分析四种采样频率下频谱的分布，在满足采样定理情况下做频谱分析。

        实验代码：

clc,clear;
%分析不同采样频率下的频谱分布
a=42;b=1;
T0=[0.001 0.0005 0.0002 0.0001 0.00005 0.00001];  %六种采样间隔
LT=10;                    %信号记录长度（秒）
for i=1:6
    T=T0(i);
    N=LT/T+1;            %信号记录点数
    n=0:N-1;
    F=1/LT;               %频率分辨率
    f=(floor(-(N-1)/2):floor((N-1)/2))*F;
    x=4*cos(100*pi*a*b*n*T)+2*cos(200*pi*a*b*n*T)+cos(300*pi*a*b*n*T);   %对模拟信号进行抽样
    X=T*fftshift(fft(x));                 %求傅立叶变换
    subplot(3,2,i),plot(f,abs(X));xlabel('模拟角频率（Hz）');
    axis([min(f) max(f) 0 inf]);           %坐标限制
    str=['T=' num2str(T) '; fs=' num2str(1/T)];title(str);  %标题显示采样间隔和采样频率 
end

        仿真结果：

 

 

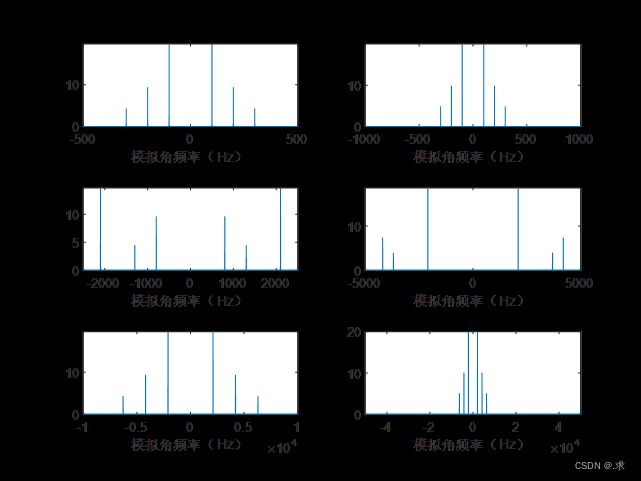
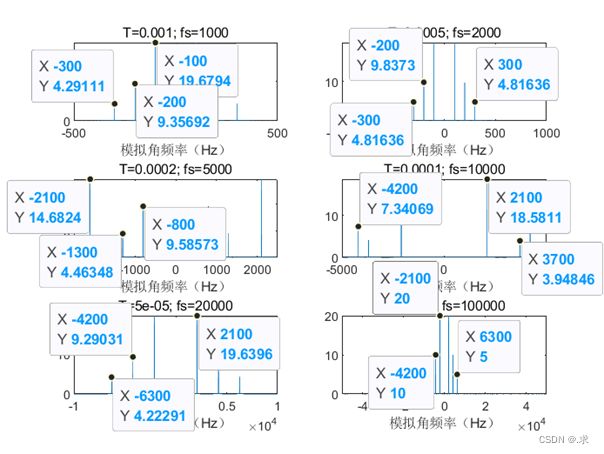
由图2和图3可知,对这6张小图进行频谱分析可得：

    a.当 时，对应图中的第一、二小图，看标注的数据可知，信号频率分量与之前推导出来的频率分量均不相等，可以知道没有过滤出任何一个频率分量。

    b.当 时，对应图中的第三小图，看标注数据可以知道，存在一个2100Hz的频率分量，即筛选出了 的频率分量，其余分量没有筛选出来。

    c.当 时，对应图中的第四小图，看标注数据可以知道，分别存在一个2100Hz的和一个4200Hz的频率分量，即筛选除了 和 的频率分量，其余分量没有筛选出来。

    d.当 时，对应图中的第五、六小图，看标注数据可以知道，分别存在一个2100Hz的、一个4200Hz的和一个6300Hz的频率分量，即筛选除了  和 的频率分量，则信号的频率分量全部筛选出来了。另，当抽样频率增大，频率分量的幅度和位置一致，与实际计算的结果一致，频谱图中最高频率即为在该抽样频率下的最高可分析频率，等于信号抽样频率的一半。

    总结:抽样频率大于2倍的信号的频率分量时，才能将该信号频率给抽样出来，其余的分量则信号失真，频率分量错误。

    ③任意生成两组有限长信号，对信号分别进行直接卷积和FFT算法求卷积，并分析圆周卷积与线性卷积的关系。

        实验代码：

clc,clear;
%对有限信号分别进行直接卷积和FFT算法求卷积
x=[1 3 1 4];          %序列x
h=[1 2 0 1 2];        %序列y
y=conv(x,h);          %线性卷积
x8=fft(x,8);H8=fft(h,8);y8=ifft(x8.*H8);             %8点循环卷积
x9=fft(x,9);H9=fft(h,9);y9=ifft(x9.*H9);             %9点循环卷积
x10=fft(x,10);H10=fft(h,10);y10=ifft(x10.*H10);      %10点循环卷积
x6=fft(x,6);H6=fft(h,6);y6=ifft(x6.*H6);             %6点循环卷积
x7=fft(x,7);H7=fft(h,7);y7=ifft(x7.*H7);             %7点循环卷积
subplot(241),stem((0:length(x)-1),x);
title('(1)原始序列x(n)');axis([0 10 0 15]);
subplot(242),stem((0:length(h)-1),h);
title('(2)原始序列h(n)');axis([0 10 0 15]);
subplot(243),stem((0:length(y)-1),y);
title('(3)线性卷积y(n)');axis([0 10 0 15]);
subplot(244),stem((0:length(y8)-1),y8);
title('(4)  8 点循环卷积y_8(n)');axis([0 10 0 15]);
subplot(245),stem((0:length(y9)-1),y9);
title('(5)  9 点循环卷积y_9(n)');axis([0 10 0 15]);
subplot(246),stem((0:length(y10)-1),y10);
title('(6)  10 点循环卷积y_1_0(n)');axis([0 10 0 15]);
subplot(247),stem((0:length(y6)-1),y6);
title('(7)  6 点循环卷积y_6(n)');axis([0 10 0 15]);
subplot(248),stem((0:length(y7)-1),y7);
title('(8)  7 点循环卷积y_7(n)');axis([0 10 0 15]);

         仿真结果：

 

由图可得 的长度为M=4，序列 的长度L=5，于是线性卷积 的长度为M+L-1=8。当循环卷积的点数N≥8时，循环卷积和线性卷积相同，见图N=8、9、10的情况；当循环卷积的点数N＜8时，此时循环卷积就是线性卷积的N点周期延拓再取N点主值序列，会产生混叠现象，不能代表线性卷积，见图N=6、7的情况。

    所以N点循环卷积代替线性卷积的条件是：

N≥M+L-1。