西瓜书习题2.5的证明

关于西瓜书中$AUC=1-l_{rank}$的推导分析

​​       在期末考试暂时告一段落之后，可以将前段时间学习《机器学习》时整理的一部分内容更新了. 在学习第二章的 $ROC$ 曲线部分时，遇到了题目中的表达式的证明的问题. 周志华老师用到了初学者深恶痛绝的几个字来完成讲解——“易得/易知”. 自己思考过程中会发现这个结论并没有那么显然.

$ROC$ 和 $AUC$ 的基础内容

$ROC$

​​       考虑一个二分类问题，我们需要找到一个学习出来的分类器模型对验证集数据进行分类为正例或反例，简单来说，我们根据某一种分类算法将所有的数据进行排序，将更可能为正例的样本排在前面，越不可能为正例的样本排在后面，然后我们可以寻得一个截断点，将截断点前的样本划分为正例，其后的样本分为反例. 这个截断点的设定很容易，通过调整阈值大小就可以自由地将其前后挪动，因此一个分类器的效果实际上是由排序效果决定的，也即是考虑分类器将多大比例的正例正确地排到了反例的前面，考虑如下的两个排序：
$$T,T,T,F,FF,T,F,T,T$$
​​       显然前面一个分类效果就强于后面的，但是总不能简简单单凭借感觉判断好坏，因此仍然要引入一些更为正式的指标. 首先将分类结果进行一个再分类：

	实际为正例	实际为反例
分类为正例	$TP$	$FP$
分类为反例	$FN$	$TN$

​ $ROC$ 曲线使用的两个指标就是真阳性率 $TPR$ 和假阳性率 $FPR$：
$$TPR=\frac{TP}{TP+FN},FPR=\frac{FP}{FP+TN}$$
二者更直观的表述为正例查全率和反例查错率. $ROC$ 曲线以 $TPR$ 为纵轴，$FPR$ 为横轴. 理论上绘制 $ROC$ 曲线应当计算每种阈值下的 $TPR$ 和 $FPR$ 再绘制图线，但这样操作过于复杂，下面考虑一种更为简单的绘制方式：

​​       现有一个学习得到的分类函数 $f(x)$ 以及一组样本 $\{(x_i,y_i){\}}_{i=1}^m$，其中有正例 $m^{+}$ 个，反例 $m^{-}$ 个. 首先我们需要根据 $f(x_i)$ 的取值将样本点排序（我们希望得到的排序是和按 $y_i$ 排序的顺序一致），然后按照下述操作绘制图线：

1. 将分类阈值调到最大，使得所有的样例均被划分为反例，此时 $TPR=FPR=0$，在图中标记点 $(0,0).$

2. 调整（减小）分类阈值，一次“放入”一个“正例”，记上次标记的点为 $(x,y)$，若这一次放入的“正例”的真实情况也为正例，则这次标记 $(x,y+\frac{1}{m^{+}})$；若为真实情况为反例，则标记 $(x+\frac{1}{m^{-}},y)$.

3. 重复步骤2直至将所有的样例全部分为正例，此时$TPR=FPR=1$，标记 $(1,1)$.

4. 连接相邻的标记点.

   特别地，如果我们遇到了同分区间，就可以直接标记同分区间起点和终点对应的点，然后将这两点相连

这样我们就可以较为方便的绘制出 $ROC$ 曲线图了.

$AUC$

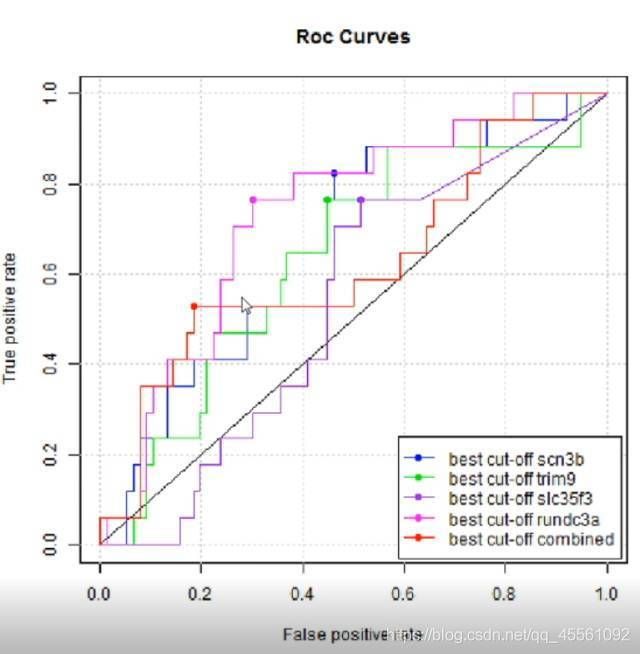
​​       接下来我们要评估不同的分类器的分类效果，实际上就是分析分类函数 $f(x)$ 对样本的排序的正确行，考虑下面的 $ROC$ 曲线图：

​​       我们可以看到很多条曲线，最靠近左上角的粉色曲线的分类效果显然强于最靠近右下角的紫色曲线，但是如何分析那些具有交错点的曲线的好坏呢？可以考虑引入另一种量度 $AUC$(Area Under $ROC$ Curve)，即 $ROC$ 曲线下方的面积大小.

​​       假设某条 $ROC$ 曲线获得的所有标记点为 $(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$，则 $AUC$ 计算公式如下：
$$AUC=\frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)(y_{i+1}+y_i)$$
​​       ​然后周志华老师给出了一个排序损失表达式$l_{rank}$：
$$l_{rank}=\frac{1}{m^{+}{m}^{-}}\sum _{x^{+}\in D^{+}}\sum _{x^{-}\in D^{-}}(\coprod (f(x^{+})<f(x^{-}))+\frac{1}{2}\coprod (f(x^{+})=f(x^{-})))$$
并且告诉我们这个表达式“很显然”地给出了 $AAC$ —— Area Above $ROC$ Curve，$ROC$ 曲线上方的面积大小，而第二章课后习题中的第5题也是要求证明 $AUC+l_{rank}=1$，接下来将给出自己整理的较为直观的证明.

证明 $AUC+l_{rank}=1$

​​​       首先给出10个样例并绘制出其对应的ROC图. 经过f(x)变换后，每个样例都获得了一个得分，按得分排序如下:

+	-	-	+	+	+	-	-	+	-
8	7	6	5	4	4	4	3	2	1

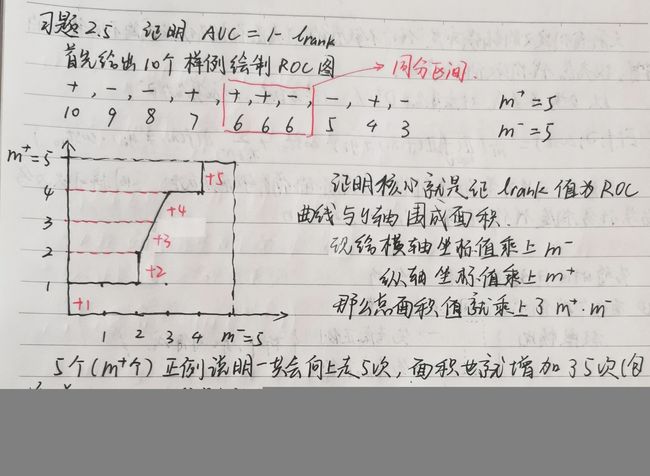
​​​       可见存在一段同分区间，最终获得的图如下：（手绘图表，不好看的话请多多包涵）

​​​       上图中为了方便绘制和计算，已经将横坐标值乘上$m^{-}$，纵坐标值乘上$m^{+}$，总面积就乘上了$m^{+}{m}^{-}$. 这样一来，我们就获得了一个 $RO{C}^{\prime }$ 曲线，其上的每个点的纵坐标就表示着被归类为“正例”的真实正例数，横坐标值表示着被归类为“正例”的真实反例数.

​​​       $AUC$ 的计算公式比较好理解，是直接基于图形计算的，考虑相邻的两点连线与横轴构成的矩形或梯形面积然后再累加求和即可得证，关键在于证明 $l_{rank}$ 表达式的值是 $ROC$ 曲线上方的面积.

​​​       5个（$m^{+}$ 个）正例说明 $RO{C}^{\prime }$ 曲线一共会向上“走”5次，曲线上方的面积也会随之增加5次，在图中已经用 $+1，+2，+3，+4，+5$ 分别表示这5次面积增加，其中每次增加的面积可记为：
$$S_{+1}=0\cdot 1,S_{+2}=2\cdot 1,S_{+3}=2\cdot 1+{\sigma }_3\cdot 1,S_{+4}=2\cdot 1+{\sigma }_4\cdot 1,S_{+5}=4\cdot 1$$
​​​       分析可知每次增加的面积可被分为增加的矩形部分面积，以及同分区间处增加的三角形部分面积，前者在所有 $+i$ 处均存在，而后者仅在同分区域存在（只有同分区间会存在斜线）

​​​       分析增加的矩形面积：对 $+i$ 而言，矩形面积为“评分”比第 $i$ 个正例高的反例个数，或者说，被排到了这个正例前的反例的个数

​​​       分析增加的三角形面积：对处于同分区间的三角形区域 ${\sigma }_3+{\sigma }_4$ 而言，其面积可以由以同分区间上正例数 $n^{+}$ 和反例数 $n^{-}$ 为直角边的三角形面积 $\frac{1}{2}{n}^{+}{n}^{-}$表示

​​​       综上我们可以推出对于第 $i$ 个正例而言，它对应的面积增加为：
$$S_{+i}=p+\frac{q}{2}$$
其中 $p$ 为得分高于这个正例的反例个数，$q$ 为得分与这个正例相同的反例个数（处于同分区间的反例个数），进而有 $RO{C}^{\prime }$ 曲线和 $ROC$ 曲线上方的面积计算公式：
$$S_{RO{C}^{\prime }}=\sum _{i=1}^{m^{+}}{S}_{+i},S_{ROC}=\frac{1}{m^{+}{m}^{-}}\cdot S_{RO{C}^{\prime }}$$
​​​       用更规范的表示方法展现：
$$\begin{gathered} p=\sum _{x^{-}\in D^{-}}\coprod (f(x^{+})<f(x^{-}))即对某个特定的x^{+}而言，所有得分高于它的反例个数 \\ q=\sum _{x^{-}\in D^{-}}\coprod (f(x^{+})=f(x^{-}))即对某个特定的x^{+}而言，所有得分与它相等的反例个数 \end{gathered}$$
​​​       故有：
$$\begin{array}{rl}{S}_{ROC}& =\frac{1}{m^{+}{m}^{-}}\sum _{x^{+}\in D^{+}}(\sum _{x^{-}\in D^{-}}\coprod (f(x^{+})<f(x^{-}))+\frac{1}{2}\sum _{x^{-}\in D^{-}}\coprod (f(x^{+})=f(x^{-})))\\ & =\frac{1}{m^{+}{m}^{-}}\sum _{x^{+}\in D^{+}}\sum _{x^{-}\in D^{-}}(\coprod (f(x^{+})<f(x^{-}))+\frac{1}{2}\coprod (f(x^{+})=f(x^{-})))\\ & =l_{rank}\end{array}$$
​​​       至此我们已经证明了两个表达式的几何含义，再通过两部分的面积和为整个 $ROC$ 曲线图的面积，就可以得到所要证明的结论 $AUC+l_{rank}=1$.

​​​       最后附上当时自己手写的证明过程.



​​​       后面可能会更新一下第三章遇到的问题的解决.