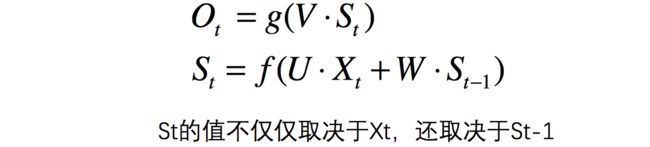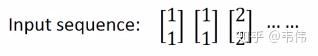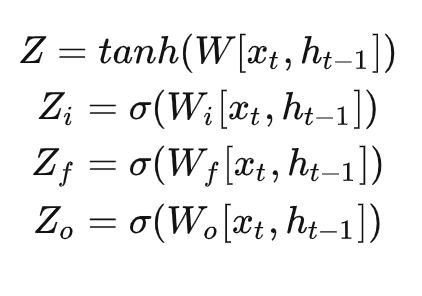数据分析-深度学习 Pytorch Day8
一。什么是循环神经网络:
循环神经网络(Rerrent Neural Network, RNN),历史啊,谁发明的都不重要,说了你也记不住,你只要记住RNN是神经网络的一种,类似的还有深度神经网络DNN,卷积神经网络CNN,生成对抗网络GAN,等等。另外你需要记住RNN的特点,RNN对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,利用了RNN的这种能力,使深度学习模型在解决语音识别、语言模型、机器翻译以及时序分析等NLP领域的问题时有所突破。
我们需要重点来了解一下RNN的特点这句话,什么是序列特性呢?我个人理解,就是符合时间顺序,逻辑顺序,或者其他顺序就叫序列特性,举几个例子:
拿人类的某句话来说,也就是人类的自然语言,是不是符合某个逻辑或规则的字词拼凑排列起来的,这就是符合序列特性。
语音,我们发出的声音,每一帧每一帧的衔接起来,才凑成了我们听到的话,这也具有序列特性、
股票,随着时间的推移,会产生具有顺序的一系列数字,这些数字也是具有序列特性。
二。为什么要发明循环神经网络:
我们先来看一个NLP很常见的问题,命名实体识别,举个例子,现在有两句话:
第一句话:I like eating apple!(我喜欢吃苹果!)
第二句话:The Apple is a great company!(苹果真是一家很棒的公司!)
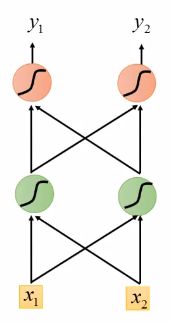
现在的任务是要给apple打Label,我们都知道第一个apple是一种水果,第二个apple是苹果公司,假设我们现在有大量的已经标记好的数据以供训练模型,当我们使用全连接的神经网络时,我们做法是把apple这个单词的特征向量输入到我们的模型中(如下图),在输出结果时,让我们的label里,正确的label概率最大,来训练模型,但我们的语料库中,有的apple的label是水果,有的label是公司,这将导致,模型在训练的过程中,预测的准确程度,取决于训练集中哪个label多一些,这样的模型对于我们来说完全没有作用。问题就出在了我们没有结合上下文去训练模型,而是单独的在训练apple这个单词的label,这也是全连接神经网络模型所不能做到的,于是就有了我们的循环神经网络。
(全连接神经网络结构)
三。循环神经网络的结构及原理:
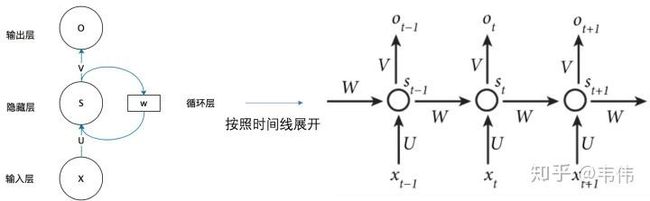
(RNN结构)
上图就是RNN的结构,我第一次看到这图的第一反应是,不是说好的循环神经网络么,起码得是神经网络啊,神经网络不是有很多球球么,也就是神经元,这RNN咋就这几个球球,不科学啊,看不懂啊!!!!随着慢慢的了解RNN,才发现这图看着是真的清楚,因为RNN的特殊性,如果展开画成那种很多神经元的神经网络,会很麻烦。
我们先来讲解一下上面这幅图,首先不要管右边的W,只看X,U,S,V,O,这幅图就变成了,如下:
等等,这图看着有点眼熟啊,这不就是全连接神经网络结构吗?对,没错,不看W的话,上面那幅图展开就是全连接神经网络,其中X是一个向量,也就是某个字或词的特征向量,作为输入层,如上图也就是3维向量,U是输入层到隐藏层的参数矩阵,在上图中其维度就是3X4,S是隐藏层的向量,如上图维度就是4,V是隐藏层到输出层的参数矩阵,在上图中就是4X2,O是输出层的向量,在上图中维度为2。有没有一种顿时豁然开朗的感觉,正是因为我当初在学习的时候,可能大家都觉得这个问题比较小,所以没人讲,我一直搞不清楚那些神经元去哪了。。所以我觉得讲出来,让一些跟我一样的小白可以更好的理解。
弄懂了RNN结构的左边,那么右边这个W到底是什么啊?把上面那幅图打开之后,是这样的:
等等,这又是什么??别慌,很容易看,举个例子,有一句话是,I love you,那么在利用RNN做一些事情时,比如命名实体识别,上图中的 ��−1 代表的就是I这个单词的向量, � 代表的是love这个单词的向量, ��+1 代表的是you这个单词的向量,以此类推,我们注意到,上图展开后,W一直没有变,W其实是每个时间点之间的权重矩阵,我们注意到,RNN之所以可以解决序列问题,是因为它可以记住每一时刻的信息,每一时刻的隐藏层不仅由该时刻的输入层决定,还由上一时刻的隐藏层决定,公式如下,其中 �� 代表t时刻的输出, �� 代表t时刻的隐藏层的值:
值得注意的一点是,在整个训练过程中,每一时刻所用的都是同样的W。
四。举个例子,方便理解:
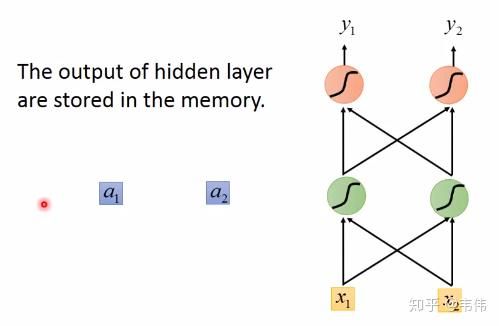
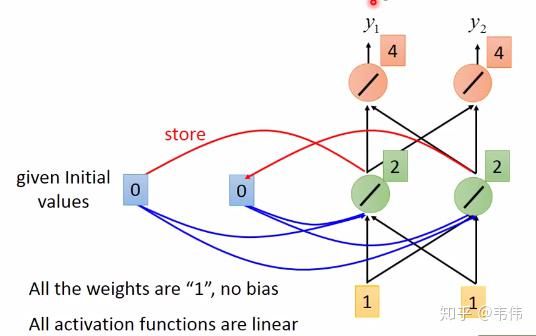
假设现在我们已经训练好了一个RNN,如图,我们假设每个单词的特征向量是二维的,也就是输入层的维度是二维,且隐藏层也假设是二维,输出也假设是二维,所有权重的值都为1且没有偏差且所有激活函数都是线性函数,现在输入一个序列,到该模型中,我们来一步步求解出输出序列:
你可能会好奇W去哪了?W在实际的计算中,在图像中表示非常困难 ,所以我们可以想象上一时刻的隐藏层的值是被存起来,等下一时刻的隐藏层进来时,上一时刻的隐藏层的值通过与权重相乘,两者相加便得到了下一时刻真正的隐藏层,如图 �1 , �2 可以看做每一时刻存下来的值,当然初始时�1 , �2是没有存值的,因此初始值为0:
当我们输入第一个序列,【1,1】,如下图,其中隐藏层的值,也就是绿色神经元,是通过公式 ��=�(�⋅��+�⋅��−1) 计算得到的,因为所有权重都是1,所以也就是 1∗1+1∗1+1∗0+1∗0=2 (我把向量X拆开计算的,由于篇幅关系,我只详细列了其中一个神经元的计算过程,希望大家可以看懂,看不懂的请留言),输出层的值4是通过公式 ��=�(�⋅��) 计算得到的,也就是 2∗1+2∗1=4 (同上,也是只举例其中一个神经元),得到输出向量【4,4】:
当【1,1】输入过后,我们的记忆里的 �1,�2 已经不是0了,而是把这一时刻的隐藏状态放在里面,即变成了2,如图,输入下一个向量【1,1】,隐藏层的值通过公式��=�(�⋅��+�⋅��−1) 得到, 1∗1+1∗1+1∗2+1∗2=6 ,输出层的值通过公式��=�(�⋅��),得到 6∗1+6∗1=12 ,最终得到输出向量【12,12】:
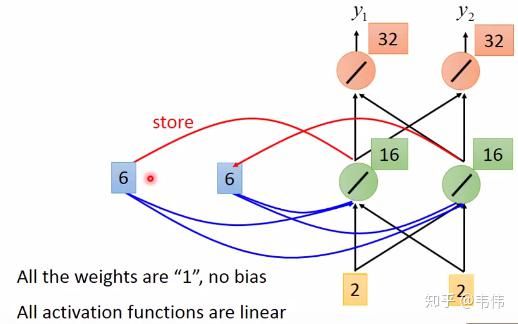
同理,该时刻过后 �1,�2 的值变成了6,也就是输入第二个【1,1】过后所存下来的值,同理,输入第三个向量【2,2】,如图,细节过程不再描述,得到输出向量【32,32】:
由此,我们得到了最终的输出序列为:
至此,一个完整的RNN结构我们已经经历了一遍,我们注意到,每一时刻的输出结果都与上一时刻的输入有着非常大的关系,如果我们将输入序列换个顺序,那么我们得到的结果也将是截然不同,这就是RNN的特性,可以处理序列数据,同时对序列也很敏感。
五。什么是LSTM:
如果你经过上面的文章看懂了RNN的内部原理,那么LSTM对你来说就很简单了,首先大概介绍一下LSTM,是四个单词的缩写,Long short-term memory,翻译过来就是长短期记忆,是RNN的一种,比普通RNN高级(上面讲的那种),基本一般情况下说使用RNN都是使用LSTM,现在很少有人使用上面讲的那个最基础版的RNN,因为那个存在一些问题,LSTM效果好,当然会选择它了!
六。为什么LSTM比普通RNN效果好?
这里就牵扯到梯度消失和爆炸的问题了,我简单说两句,上面那个最基础版本的RNN,我们可以看到,每一时刻的隐藏状态都不仅由该时刻的输入决定,还取决于上一时刻的隐藏层的值,如果一个句子很长,到句子末尾时,它将记不住这个句子的开头的内容详细内容,具体原因可以看我之前写的文章,如下:
韦伟:从反向传播推导到梯度消失and爆炸的原因及解决方案(从DNN到RNN,内附详细反向传播公式推导)703 赞同 · 33 评论文章
LSTM通过它的“门控装置”有效的缓解了这个问题,这也就是为什么我们现在都在使用LSTM而非普通RNN。
七。揭开LSTM神秘的面纱:
既然前面已经说了,LSTM是RNN的一种变体,更高级的RNN,那么它的本质还是一样的,还记得RNN的特点吗,可以有效的处理序列数据,当然LSTM也可以,还记得RNN是如何处理有效数据的吗,是不是每个时刻都会把隐藏层的值存下来,到下一时刻的时候再拿出来用,这样就保证了,每一时刻含有上一时刻的信息,如图,我们把存每一时刻信息的地方叫做Memory Cell,中文就是记忆细胞,可以这么理解。
打个比喻吧,普通RNN就像一个乞丐,路边捡的,别人丢的,什么东西他都想要,什么东西他都不嫌弃,LSTM就像一个贵族,没有身份的东西他不要,他会精心挑选符合自己身份的物品。这是为什么呢?有没有思考过,原因很简单,乞丐没有选择权,他的能力注定他只能当一个乞丐,因此他没有挑选的权利,而贵族不一样,贵族能力比较强,经过自己的打拼,终于有了地位和身份,所以可以选择舍弃一些低档的东西,这也是能力的凸显。
LSTM和普通RNN正是贵族和乞丐,RNN什么信息它都存下来,因为它没有挑选的能力,而LSTM不一样,它会选择性的存储信息,因为它能力强,它有门控装置,它可以尽情的选择。如下图,普通RNN只有中间的Memory Cell用来存所有的信息,而从下图我们可以看到,LSTM多了三个Gate,也就是三个门,什么意思呢?在现实生活中,门就是用来控制进出的,门关上了,你就进不去房子了,门打开你就能进去,同理,这里的门是用来控制每一时刻信息记忆与遗忘的。
依次来解释一下这三个门:
Input Gate:中文是输入门,在每一时刻从输入层输入的信息会首先经过输入门,输入门的开关会决定这一时刻是否会有信息输入到Memory Cell。
Output Gate:中文是输出门,每一时刻是否有信息从Memory Cell输出取决于这一道门。
Forget Gate:中文是遗忘门,每一时刻Memory Cell里的值都会经历一个是否被遗忘的过程,就是由该门控制的,如果打卡,那么将会把Memory Cell里的值清除,也就是遗忘掉。
按照上图的顺序,信息在传递的顺序,是这样的:
先经过输入门,看是否有信息输入,再判断遗忘门是否选择遗忘Memory Cell里的信息,最后再经过输出门,判断是否将这一时刻的信息进行输出。
八。LSTM内部结构:
抱歉最近事比较多,没有及时更新。。让我们先回顾一下之前讲了点啥,关于LSTM,我们了解了它的能力比普通RNN要强,因为它可以对输入的信息,选择性的记录或遗忘,这是因为它拥有强大的门控系统,分别是记忆门,遗忘门,和输出门,至于这三个门到底是如何工作的,如何起作用的。本节我们就来详细讲解LSTM的内部结构。
在了解LSTM的内部结构之前,我们需要先回顾一下普通RNN的结构,以免在这里很多读者被搞懵,如下:
我们可以看到,左边是为了简便描述RNN的工作原理而画的缩略图,右边是展开之后,每个时间点之间的流程图,注意,我们接下来看到的LSTM的结构图,是一个时间点上的内部结构,就是整个工作流程中的其中一个时间点,也就是如下图:
注意,上图是普通RNN的一个时间点的内部结构,上面已经讲过了公式和原理,LSTM的内部结构更为复杂,不过如果这么类比来学习,我认为也没有那么难。
我们类比着来学习,首先看图中最中间的地方,Cell,我们上面也讲到了memory cell,也就是一个记忆存储的地方,这里就类似于普通RNN的 �� ,都是用来存储信息的,这里面的信息都会保存到下一时刻,其实标准的叫法应该是 ℎ� ,因为这里对应神经网络里的隐藏层,所以是hidden的缩写,无论普通RNN还是LSTM其实t时刻的记忆细胞里存的信息,都应该被称为 ℎ� 。再看最上面的 � ,是这一时刻的输出,也就是类似于普通RNN里的 �� 。最后,我们再来看这四个 �,��,��,�� ,这四个相辅相成,才造就了中间的Memory Cell里的值,你肯恩要问普通RNN里有个 �� 作为输入,那LSTM的输入在哪?别着急,其实这四个 �,��,��,�� 都有输入向量 �� 的参与。对了,在解释这四个分别是什么之前,我要先解释一下上图的所有这个符号,
都代表一个激活函数,LSTM里常用的激活函数有两个,一个是tanh,一个是sigmoid。
�=���ℎ(�[��,ℎ�−1])��=�(��[��,ℎ�−1])��=�(��[��,ℎ�−1])��=�(��[��,ℎ�−1])
其中 � 是最为普通的输入,可以从上图中看到, � 是通过该时刻的输入 �� 和上一时刻存在memory cell里的隐藏层信息 ℎ�−1 向量拼接,再与权重参数向量 � 点积,得到的值经过激活函数tanh最终会得到一个数值,也就是 � ,注意只有 � 的激活函数是tanh,因为 � 是真正作为输入的,其他三个都是门控装置。
再来看 �� ,input gate的缩写i,所以也就是输入门的门控装置, �� 同样也是通过该时刻的输入 �� 和上一时刻隐藏状态,也就是上一时刻存下来的信息 ℎ�−1 向量拼接,在与权重参数向量 �� 点积(注意每个门的权重向量都不一样,这里的下标i代表input的意思,也就是输入门)。得到的值经过激活函数sigmoid的最终会得到一个0-1之间的一个数值,用来作为输入门的控制信号。
以此类推,就不详细讲解 ��,�� 了,分别是缩写forget和output的门控装置,原理与上述输入门的门控装置类似。
上面说了,只有 � 是输入,其他的三个都是门控装置,负责把控每一阶段的信息记录与遗忘,具体是怎样的呢?我们先来看公式:
首先解释一下,经过这个sigmod激活函数后,得到的 ��,��,�� 都是在0到1之间的数值,1表示该门完全打开,0表示该门完全关闭,