Logistic Regression -- 单自变量

Why

传统的回归过程如线性回归解决的是 Y 为连续实数的情况。Logistic 回归是解决离散的分类问题，换句话说，要求Y是0或者1。
名字来自于指数分布家族中的Logistic 分布。

What

我们处理的是0-1分类问题. 输入n个样本, 第 i 个样本为Xi,Yi. Xi 是有限的离散空间, Yi 是 0 或1. 当 X=xi , Yi=1 发生的概率为 P(Yi=1|Xi=xi;β) . 让 pi=P(Yi=1|Xi=xi;β) , 则 1−pi=P(Yi=0|Xi=xi;β) 且 π(xi)=E(Yi|Xi;β)=pi=F(zi) . zi 是以 β 为参数的有关 Xi 的函数. 我们知道这是伯努利分布 Yi∼B(1,p) , F(zi)=pi 是累计分布函数.
让它更具体一些, 设 pi=P(Yi=1|Xi=xi;β)=ezi1+ezi=F(zi) 。具体针对回归问题来说，假设model是最简单的对X线性的Logistic regression， 则 Y=1 事件发生的概率/比例/proportion为 p=P(Y=1|X=x;β)=ez1+ez∈[0,1]→z=log(p1−p)=β0+β1x. F(Z)=p 形状是从0到1的S型.
通过 p 寻找z的过程也叫做logit变换( logit(p)=lnp1−p ), 得出的 z=β0+β1x 毫无疑问是一条直线。所以Logistic regression 用一条直线来拟合做过logit变换后的proportion。 得出直线后我们再带入 xi 到 p 即可做prediction了. 我们再对输出pi取一个阀值(e.g. 0.5), 当 p≤0.5 时 Yi 是0, 反之为1.

注: 其实不局限于用直线做拟合`, 只要是linear in parameters 的linear regression即可.

How

例子

图中所示为某城市心脏病数据。

左手边列表示年龄段，右手边表对应年龄段中有心脏病的比例(占样本中的)。能看到随着年龄增长心脏病比例也相应增高.
设 π(X)=p 表年龄为 X 的人口中有心脏病的所占比例，取年龄段中点为该年龄段的代表年龄。以π(X)为数轴, X 为横轴作图能看到呈S型(见下图), 因此我们可以考虑用Logistic Regression做拟合, 即用直线β0+β1X对做了Logit变换后的 π′(X) 建模. 这种模型叫做”Logistic Linear Model”.

当我们找出合适的直线后, 对要预测的 X 带入π(X)=exp(β0+β1X)/[1+exp(β0+β1X)]即是我们想要的预测值.

比如我们算得 β0≈−8.467,β1≈0.157 . 我们要预测 X=45 时得心脏病的比例是多少. 很简单,
π(45)=exp(β0+β145)/[1+exp(β0+β145)]=0.1957 . 可以看到和图中[40, 50)的数据很吻合.

特别说明下, 拟合时输入的样本是连续的, 是我们把换成了离散的 即proportion. 在预测时同样需要用取中指的方法换算成离散的计算proportion.

为什么不直接用线性回归做拟合

我们看到S型似乎和直线差不多, 那为毛不直接用线性回归呢? 原因有二
1. 线性回归无法保证 π(X)∈[0,1] . 即使对于我们感兴趣的数据用线性拟合的结果或许也在 [0,1] 之间, 但我们要追求概念上的正确, 而不只是满足于在特定数据上的正确.
2. 线性回归中假设 Y/ϵ∼N(0,σ2) , 而Logistic 回归中并不假设每个 π(X) 有相同的方差, 而是说 π 符合伯努利分布. 因此 var(Yi)=πi(1−πi) , 对不同的 Yi 并不是常数.

Odds

定义 odds=π(X)/(1−π(X)). 因此logit 变换相当于 log(odds). 对于简单线性模型有 π(X)/(1−π(X))=exp(β0+β1X) . 基于Odds我们再定义Odds的比例为 Odds at X + 1Odds at X=π(X+1)/(1−π(X+1))π(X)/(1−π(X)) . 拿我们上节用到的例子来说 Odds at age X + 1Odds at age X=π(X+1)/(1−π(X+1))π(X)/(1−π(X))=eβ1 . 我们可以看到, 对于Logistic Linear Model, odds ratio是常数, 与 X 无关 .

Odds ratio有什么用呢? 它表明了当X增加了 1 时odds的变化.

如何估算β

对于线性回归我们用最小二乘法来计算 β^ . 但高斯-马尔科夫定理告诉我们使用最小二乘法的一个前提是 Y 的方差要相等. 而Logistic Regression我们由于使用的是伯努利分布, 方差不满足条件, 所以我们回到统计中估算参数的最基本方法: 最大似然法.

在用最大似然法之前我们先要明确π(X)到底是符合什么分布. 我们知道 π(X) 实际上是条件概率, 拿之前例子说话, 我们算的其实是 π(45)=P(Y=1|X=45) , 是不是觉得这样的条件概率很眼熟? 没错, 因为 Y 只有两种情况, 自然要使用伯努利分布! 所以πi(第i个样本对应的比例)的pmf为 πYii(1−πi)1−Yi , 因此Likelihood L=∏n1=1πYii(1−πi)1−Yi , 用Log-likelihood把乘法变加法 logL=∑[Yiπi+(1−Yi)log(1−πi)] . 对于简单线性问题,
logL(β0,β1)=∑n1[Yilogπi+(1−Yi)log(1−πi)]=∑n1[Yilog(πi/(1−πi)+log(1−πi)]=∑n1[Yi(β0+β1Xi)+log(1−πi)]=∑n1[Yi(β0+β1Xi)−∑n1log(1+exp(β0+β1Xi)].
为了求 max LogL, 对之以 β0,β1 求偏导并使之等于0, 得 ∑πi=∑Yi,∑πiXi=∑πiYi. 然而和Lasso一样, 我们算不出 β0^,β1^ 的具体形式, 而是采用循环方法算得numerical 解. 最后带入, 得 π^i=exp(β0^+β1^X)/[1+exp(β0^+β1^X)] .
当我们用矩阵表示 π′=Xβ, X 是n×2 的矩阵. Likelihood等式可写成 XT(Y−π^)=0 . 对于多变量情况, X 是n×p矩阵, 方法一致. 同样解是numerical 的approximation. 我们知道 E(β^)≈β,σ2(β^)=Cov(β^)≈(XTWX)−1 . 其中 W 是对角矩阵, 对角上的元素分别为π1(1−π1),π2(1−π2),...,πn(1−πn), 我们用拟合结果 π1^(1−π1^),π2^(1−π2^),...,πn^(1−πn^) 估算 W 得到W^. 因此 β^ 的协方差矩阵估算为 s2(β^)=(XTW^X)−1 .

尽管我们无法得到 β^j 的精确分布, 但当样本空间n非常大时, (β^j−βj)/s(βj^)∼N(0,1) . 因此approximate置信空间为 β^±z(1−α/2)s(βj^).

R中实现

glm(formula = Y ~ X, family = binomial)

模型诊断

由于 Yi∼B(1,πi) , 我们没必要再像线性回归那样检查方差是否为常数. 但是我们需要检查数据是否满足Logistic Linear Model的假设. 怎么查呢? 上节我们提到当样本空间足够大时, β^0−β0s(β^0)∼N(0,1),β^1−β1s(β1)^∼N(0,1) , 所以 E(β0^)≈β0,E(β1^)≈β1.
因此 πi^≈πi. 又因为 E(Yi)=πi.⇒E(Yi−πi)=0 . 所以当样本空间很大时, E(Yi)≈πi^⇒E(Yi−πi^)≈0. 基于此我们可以构建相应的诊断: 如果Logistic Model是合理的, 我们将看到 [Yi−πi^] 以 0 为中心轻微浮动.

基于以上思想, 有两种方法利用residuals. 在解释 之前我们先 回顾下在线性回归中我们是如何利用residual算model的 SSE=∑e2i 以 (1) 衡量拟合值与真实样本值的差距 (2) 在Reduced Model 和Full Model 之间做Hypothesis test. 在Logistic model 中我们遵循同样的思想.
1. Pearson Residual rPi=(Yi−πi^)/π^i(1−π^i)−−−−−−−−√ 因为 π^i(1−π^i) 是variance, Pearson 相当于是standardized 版residual. 由于 Yi 并不符合正太分布, 要使用half-normal plot来刻画residual. 它并不是检查是否符合正态分布, 而是看是否存在严重偏离于直线以及是否存在outlier.
2. Deviance Residual devi=sign(Yi−πi^)−2[Yilog(π^)i+(1−Yi)log(1−π^i)−−−−−−−−−−−−−−−−−−−−−−−−−−−√].

我们能看到Pearson residual中规中矩的用 Yi−πi^ 衡量拟合值和真实值之间的差距. 让 P2=∑r2pi . 但deviance 就让人摸不找头脑了. 其实只要看到deviance我们就联想到likelihood. Deviance并不直接比较 Yi 和 πi^ 的值, 而是比较likelihood. 它相当于使用了线性回归中 SSE 的第二种思想, 分别计算full model (saturated model)和reduced model的likelihood做比较. 在线性回归中我们用包含了所有自变量的作为full model, 把删去某些自变量的model作为reduced model. 那么我们就要问了, 在simple logistics 里只有一个变量哪来的full model和reduced model呢? 在simple logistics 里我们直接把我们要得到的待评估model作为reduced model, 而把没有做任何假设的作为full model
. 回顾下在估算 β 时我们用到的likelihood, pmf =πYii(1−πi)1−Yi , Likelihood L=∏n1=1πYii(1−πi)1−Yi . 因此定义 full model 的likelihood优化目标 L(F)=maxπ is in the full modelL , reduced model 为 L(R)=maxπ is in the reduced modelL . 我们要找的是likelihood比例关系 L(R)L(F). 如果reduced model拟合的足够好, 那么 L(R)L(F)≈1 等价于 logL(R)L(F)≈0 . 因此 G2=residual deviance=∑dev2=−2[log(L(R))−log(L(F))]=−2logL(R)L(F). 为了计算 G2 , 需要对 L 算两次最大化, 一次对full model, 一次对reduced model. −2是为了计算方便, 没有特殊意义. 如果 G2 很小, 说明model对数据拟合得很好. 那什么时候算很小呢? 我们可以做hypothesis test.

尽管 P2,G2 并不严格符合 χ2 分布, 但当 n 足够大时, 我们仍可以用χ2表来判断 P2,G2 是否过高.

我们也可以把这两种residuals 画出来. 一般来说每种residual的图都含有两条平行线. 然而这两条平行线并没有告诉我们什么有用信息. 换个思路我们直接画Person residual的散点图, 相当于画scale后的 Yi−πi^ 的散点图, 并对residual的散点图做局部线性拟合(loess). 如前文所说, 当residual在0附近轻微浮动时说明model拟合的不错. 如图所示

例2. 当 Xβ 不再是以 X 的一次函数时

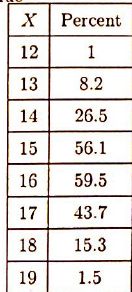
看到porpotion先增大后降低. 明显不符合S型. 画出来后如下图所示,

右图是Z的变化趋势, 是个二次项函数. 所以我们把 Xβ=β0+β1(X−X¯)+β11(X−X¯)2. 因为有平方项, 所以我们对 X 做了去中心以免计算时因为强关联性出现numerical error.
我们分别对X=13,14,17,18时计算odds, 为 0.096,0.5,0.68,0.162. 在二次时odds ratio不再是常数.

当 Y 是Yij时..

什么意思呢? 在之前我们的输入是. 现在变成 . 相当于 X 是离散的, 在每个离散的类别里有nj个observations (Y). 如 X2=53, 有 n2=60 个对应的 binary output Yi2,i=1,...,n2. 每个 Yij∼Bernoulli(0,πj) . 那么 Y.j=∑iYij∼Binomial(nj,πj).

举例说明, 假设一共有 c 种杀虫剂作自变量X1,...,Xc; nj 为暴露在 Xj 杀虫剂下虫子的个数.

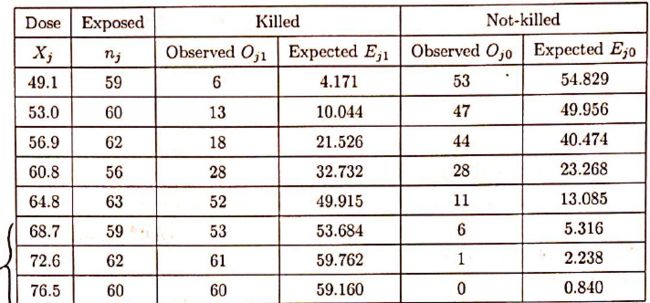
我们用线性函数对logit后 πj 做拟合 πj=β0+β1Xj,j=1,...,c=8. Yij=1 表对应虫子被干掉, 反之没有.