Python机器学习:一元回归
→ \rightarrow →回归效果评价
一元回归
一元回归主要研究一个自变量和一个因变量之间的关系,而这个自变量和因变量之间的关系又可分为线性回归和非线性回归。
⭐️ 一元线性回归分析两个变量之间的线性关系,如 y = k x + b y=kx+b y=kx+b中 x x x和 y y y就是线性关系。
⭐️ 一元非线性回归分析两个变量之间的非线性关系,如指数关系、对数关系等。
一元线性回归
下面用Iris数据集中的PetalLengthCm和PetalWidthCm两个变量来建立一元线性回归模型。
在建立模型前,我们要先知道一元线性回归分析法的预测模型: y = a x + b y=ax+b y=ax+b,我们要求的就是参数a和b,可以由下列公式求得:
a = n ∑ x i y i − ∑ x i ∑ y i n ∑ x i 2 − ( ∑ x i ) 2 a = \frac{n\sum x_iy_i-\sum x_i\sum y_i}{n\sum x_i^2-(\sum x_i)^2} a=n∑xi2−(∑xi)2n∑xiyi−∑xi∑yi
b = ∑ y i n − a ∑ x i n b = \frac{\sum y_i}{n}-a\frac{\sum x_i}{n} b=n∑yi−an∑xi
第一种
原谅我只在这里自己实现求回归方程,因为其它的太难了0.0
import pandas as pd
from matplotlib import pyplot as plt
# 中文显示问题
import seaborn as sns
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
def add_up(data): # 累加函数
sum = 0
for i in range(len(data)):
sum += data[i]
return sum
def cal_a(x,y): # 求a
a = (len(x) * add_up(x * y) - add_up(x) * add_up(y)) / (len(x) * add_up(x ** 2) - add_up(x) ** 2)
return a
def cal_b(x,y,a): # 求b
b = add_up(y) / len(x) - a * add_up(x) / len(x)
return b
a = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv") # 读取数据
x = a.PetalLengthCm # 读取x的数据
y = a.PetalWidthCm # 读取y的数据
a = cal_a(x,y) # 计算a
b = cal_b(x,y,a) # 计算b
print(a,b)
plt.figure(figsize = (10,6))
plt.scatter(x,y,c = "blue") # 原始数据的点
plt.plot(x,a * x + b,"r-",linewidth = 3) # 预测的模型
plt.xlabel("PetalWidthCm")
plt.ylabel("PetalLengthCm")
plt.title("一元线性回归模拟拟合曲线")
plt.grid()
plt.show()
第二种
现在我们再来使用python花里胡哨的包来实现一下:
import pandas as pd
import statsmodels.formula.api as smf
import seaborn as sns
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
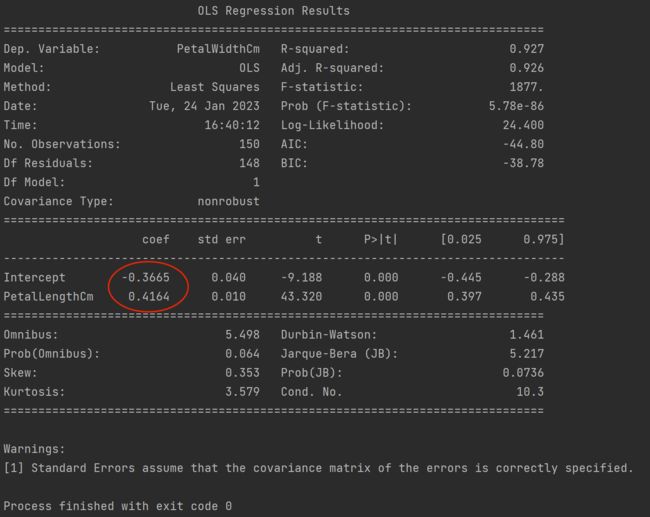
model = smf.ols("PetalWidthCm~PetalLengthCm",data = data).fit()
print(model.summary())
针对于回归模型的残差,可以使用Q-Q图来检验是否服从正态分布(关于Q-Q图是什么,可以看一下我这篇博客 → \rightarrow →假设检验)。
import pandas as pd
from matplotlib import pyplot as plt
import statsmodels.formula.api as smf
import statsmodels.api as sm
import seaborn as sns
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
model = smf.ols("PetalWidthCm~PetalLengthCm",data = data).fit()
fig = plt.figure(figsize = (14,6))
plt.subplot(1,2,1) # 将画布分为一行两列,现在对从上到下从左到右第一部分进行绘图
plt.hist(model.resid,bins = 30) # 绘制直方图
plt.grid()
plt.title("回归残差分布直方图")
ax = fig.add_subplot(1,2,2) # 现在对第二部分进行绘图
sm.qqplot(model.resid,line = "q",ax = ax)
plt.title("回归残差Q-Q图")
plt.show()
针对获得的回归模型,可以使用predict()函数对新的数据进行预测:
import pandas as pd
from matplotlib import pyplot as plt
import statsmodels.formula.api as smf
import numpy as np
import seaborn as sns
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
model = smf.ols("PetalWidthCm~PetalLengthCm",data = data).fit()
X = pd.DataFrame(data = np.arange(0.5,8,step = 0.1),columns = ["PetalLengthCm"])
Y = model.predict(X)
data.plot(kind = "scatter",x = "PetalLengthCm",y = "PetalWidthCm",c = "blue",figsize = (10,6)) # 绘制原始数据
plt.plot(X,Y,"r-",linewidth = 3) # 绘制回归模型
plt.grid()
plt.title("一元线性回归模型拟合曲线")
plt.show()
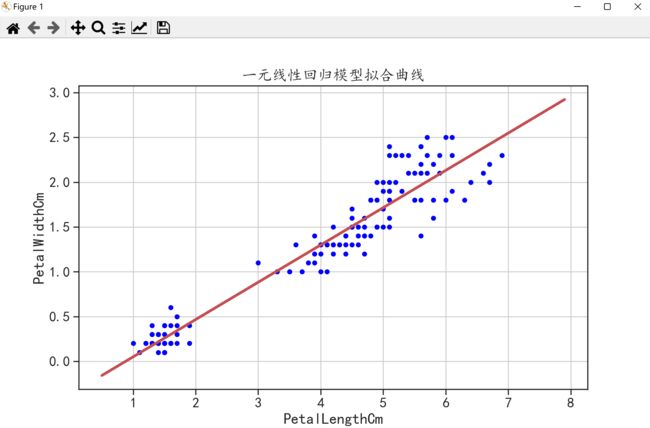
可以看到,上图跟第一种方法绘制出来的图是一样的,只是横纵坐标的区间不一样。
一元非线性回归
下面读取一组非线性数据,来进行操作。
这个数据部分内容如下:
因为它是非线性的,所以我们先绘制一个散点图,看看它比较符合哪种非线性的形式。
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap5/xydata.csv")
plt.figure(figsize = (10,6))
plt.plot(data.x,data.y,"ro")
plt.grid()
plt.show()
第一种分析
仔细一看,好像还挺符合指数关系的,那么我们还是先给出它的非线性预测模型: y = a e − b x + c y=ae^{-bx}+c y=ae−bx+c。因为这个模型的参数比较多且难以计算,在这我们可以通过curve_fit()函数利用数据对其进行参数估计来获取预测模型的参数值。
import numpy as np
import pandas as pd
from scipy.optimize import curve_fit
import seaborn as sns
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
def func(x,a,b,c):
return a * np.exp(-b * x) + c
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap5/xydata.csv")
popt,pcov = curve_fit(func,data.x,data.y) # 将预测模型的函数传给curve_fit
print("a,b,c的估计值值为:",popt)
⭐️ popt:是一个数组,存有参数的最佳值,以使得平方残差之和最小。
⭐️ pcov:是一个二维阵列,popt的估计协方差。
![]()
于是我们可以得到这个曲线的回归方程: y = − 0.1947 e − 0.1779 x + 0.6524 y=-0.1947e^{-0.1779x}+0.6524 y=−0.1947e−0.1779x+0.6524
得到回归方程后,我们就可以将其可视化,分析拟合曲线与原始数据之间的关系。
⭐️ plt.hlines():画一条水平线,参数y是控制水平线的位置,参数xmin是水平线的起始位置,参数xmax是水平线的结束位置。
import numpy as np
import pandas as pd
from scipy.optimize import curve_fit
from matplotlib import pyplot as plt
import seaborn as sns
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
def func(x,a,b,c):
return a * np.exp(-b * x) + c
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap5/xydata.csv")
popt,pcov = curve_fit(func,data.x,data.y)
a = popt[0]
b = popt[1]
c = popt[2]
fit_y = func(data.x,a,b,c) # 求得回归方程中的y
res = fit_y - data.y # 回归方程中的y减去原始数据的y为残差
plt.figure(figsize = (14,6))
plt.subplot(1,2,1) # 开始画第一个图
plt.plot(data.x,data.y,"ro",label = "原始数据") # 画原始数据
plt.plot(data.x,fit_y,"b-",linewidth = 3,label = "指数函数") # 画回归方程
plt.grid()
plt.legend() # 一个小格子,表明圆点代表原始数据,线条代表指数函数
plt.title("拟合效果")
plt.subplot(1,2,2) # 开始画第二个图
plt.plot(res,"ro") # 绘制残差点
plt.hlines(y = 0,xmin = -1,xmax = 41,linewidth = 2) # 画一条水平线
plt.grid()
plt.title("拟合残差大小")
plt.show()
第二种分析
同样,针对前面的非线性数据,它的可视化图像如下;
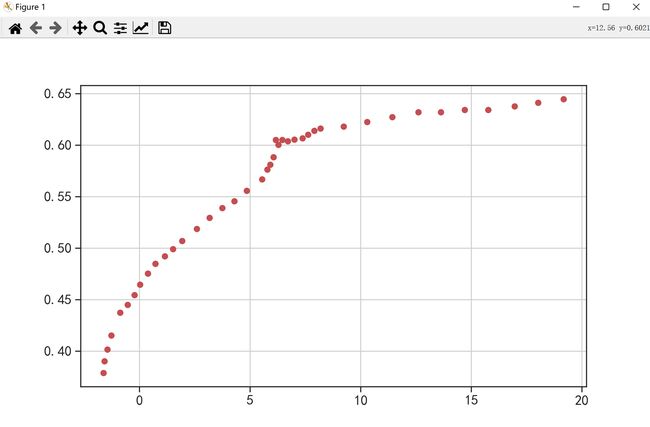
有没有这样一种可能,它的变化趋势接近于 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c呢?现在我们就来试一下看。
因为只需改一下func中的内容即可,这里就不放全部代码了。
def func(x,a,b,c):
return a * x ** 2 + b * x + c

得到的回归方程为: y = − 0 , 000978 x 2 + 0.02748 x + 0.45396 y=-0,000978x^2+0.02748x+0.45396 y=−0,000978x2+0.02748x+0.45396
下面我们再将其可视化来分析拟合曲线与原始数据之间的关系。
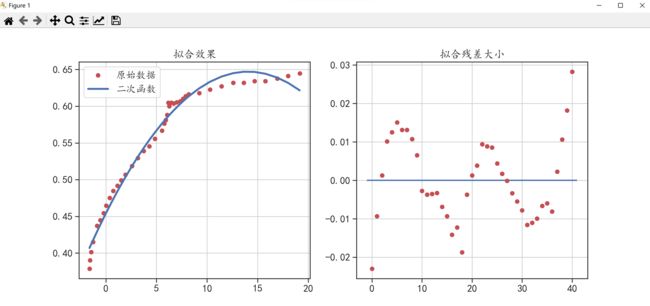
对比两次的可视化图可以发现,使用二次函数的拟合效果没有使用指数函数的拟合效果好。
所以对于一元回归来说,要得到它的回归方程,我们可以先定义一个方程,然后利用curve_fit()函数进行方程的拟合,求得参数的值,最后再带入我们预先考虑好的模型里就能得到回归方程了,这是最简单的一种。当然也可以自己用代码去实现这个功能0.0,不过对于我来说难度就很大了,还需多多努力!!