高光谱目标检测论文学习(6)—— Bayesian Constrained Energy Minimization for Hyperspectral Target Detection
前言
之前我们我们学习了HCEM和ECEM两种CEM的改进方法,这两种方法的相同点是都考虑了实际情况,加入了非线性检测的部分,从而提升了检测性能,不同的是一个主要是采用分层迭代的思想,一个采用集成学习、级联检测的思想。在这一篇文章中我们重点介绍一种新的方法BCEM,这是一种利用贝叶斯的思想去优化改进目标光谱,从而达到提升检测性能的目的。
思路
回顾我们之前提过的几种CEM变种方法,他们都是默认给定的目标光谱是准确的,而对实际高光谱图像来说,给定的目标光谱不一定就是完全精准且适合这张图像的目标光谱。
导致这种结果的原因有两点:一是因为可能给定的目标光谱本身就包含着一些噪声;二是因为实际采集到的高光谱图像受到一些环境和传感器等因素的影响,所以给定的目标光谱可能和实际图像的目标光谱不匹配。
针对这个问题,解决思路就很清晰了——我们可以对目标光谱进行改进,使其更符合实际的高光谱图像。
怎么得到实际的高光谱图像呢?这篇文章采用的思路是让真实的目标光谱作为一个中间变量,然后采用参数估计方法,估计出目标光谱的一个近似的后验概率分布,进而通过这个后验概率分布来得到真实的目标光谱。得到真实目标光谱后,再使用前一篇文章提到的regularized CEM进行检测。由于这个估计真实目标光谱的过程借鉴了贝叶斯的思想,因此将这个方法称为贝叶斯CEM(BCEM)。
检测结果的表达
对于一张高光谱图像 X X X中的一个像素 x i x_i xi,已经给定的目标光谱为 t o b s t_{obs} tobs,那么对于这个图像直接使用CEM的检测结果(或者检测得分)就可以表示成:
![]()
其中 w ( λ ) ∗ w(\lambda)^{*} w(λ)∗也就是我们提到的regularized CEM的检测器的表示形式:
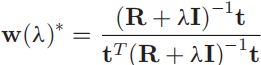
现在我们把需要估计的真实目标光谱设为 t t r u e t_{true} ttrue,直接获得这个 t t r u e t_{true} ttrue是非常困难的,因此我们以已知的 t o b s t_{obs} tobs作为基础来估计 t t r u e t_{true} ttrue。这样一来我们就需要用到一个条件概率 p ( t t r u e ∣ t o b s ) p(t_{true}|t_{obs}) p(ttrue∣tobs)。到这里我们可以采用两种方式去估计这个p,第一种方式是采用点估计的方法,直接准确的估计出一个p值,然后直接将这个p值与 t o b s t_{obs} tobs相乘得到准确的 t t r u e t_{true} ttrue;第二种方法则是去估计p的概率密度分布,然后利用积分的的方法得到最后的 t t r u e t_{true} ttrue。本文采用的是第二种方法,这是因为与点估计相比,分布的估计不仅仅以目标光谱为基础,还将目标光谱可能遵从的分布也纳入了考量,这样能够更加有效的处理结果的不确定性。
因此使用真实目标光谱 t t r u e t_{true} ttrue的得分就可以记为 f ~ ( x i ∣ t t r u e , λ ) \tilde{f}(x_i|t_{true},\lambda) f~(xi∣ttrue,λ),这个值可以表示为:

概率分布的近似
现在的问题是, p ( t t r u e ∣ t o b s ) p(t_{true}|t_{obs}) p(ttrue∣tobs)的求解还是很困难,因此需要进一步简化近似。这篇文章采用的简化近似思想是一种分期不断变化的推断方式,借助Dirichlet分布去近似估计 p ( t t r u e ∣ t o b s ) p(t_{true}|t_{obs}) p(ttrue∣tobs),将其近似为 q ( t ∣ t o b s , α ) q(t|t_{obs},\alpha) q(t∣tobs,α)。其中 α \alpha α是Dirichlet分布 G ∼ D P ( α , G 0 ) G \sim DP(\alpha,G_0) G∼DP(α,G0)的参数。
那么什么是Dirichlet分布呢?简单来说,Dirichlet分布是一种“分布的分布”,由两个参数 α \alpha α和 G 0 G_0 G0确定,其中 α \alpha α是分布参数,其值越大,分布越接近于均匀分布,其值越小,分布越集中; G 0 G_0 G0是基分布。我们也可以用一个黑盒子来理解Dirichlet分布:

在这篇文章中,我们把基分布设为以 t o b s t_{obs} tobs为均值的的高斯分布 G 0 G_0 G0,方差与置信度有关,置信度越高则方差越小。因此基分布 G 0 G_0 G0就可以表示为 G 0 ∼ N ( t o b s , v a r ) G_0 \sim N(t_{obs},var) G0∼N(tobs,var)。我们假定近似的真实目标光谱 t t t服从Dirichlet分布 G ∼ D P ( α , G 0 ) G \sim DP(\alpha,G_0) G∼DP(α,G0)。因此, p ( t t r u e ∣ t o b s ) p(t_{true}|t_{obs}) p(ttrue∣tobs)就可以近似为 q ( t ∣ t o b s , α ) q(t|t_{obs},\alpha) q(t∣tobs,α)。因此上一部分的检测得分就可以近似表示为:

插曲:Beta分布与Dirichlet分布
我们在上一部分是按照文章中所说对Dirichlet分布做了一个简要的介绍,但是这些信息还不足以让我们理解这个分布,因此在这里多作一些说明。
在介绍Dirichlet分布之前,我们首先先认识另一种分布——Beta分布。和Dirichlet分布一样,Beta分布也用来描述“分布的分布”,也就是说可以Beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出所有概率出现的可能性大小。
具体来说,Beta分布可以记为:
![]()
其中B(a,b)是Beta函数,也就是说,这个分布是由参数a和b共同确定的,a和b中包含着一些先验信息。举个例子,假设我们来估计一枚硬币掷到正面的概率,那么a就可以是掷到正面的次数,b则是掷到反面的次数。
Beta分布还有一个很特殊的性质,用Beta分布来模拟先验分布之后,通过贝叶斯推断,得到的后验分布依然是Beta分布。即:
![]()
这怎么理解呢?还是回到哪个掷硬币的例子,假设我们知道一般来说一枚硬币掷到正面的概率是0.5,那么我们就可以设a=5,b=5,这样一来掷到正面的期望就是 a a + b = 5 5 + 5 = 0.5 \frac{a}{a+b}=\frac{5}{5+5}=0.5 a+ba=5+55=0.5。之后我们又进行了三次实验,得到的结果都是正面,那么这个实验结果我们就记为(3,0),做了三次实验后,Beta分布就变为了:Beta(5,5)+(3,0)=Beta(8,5)。这时期望变成了 8 8 + 5 = 0.616 \frac{8}{8+5}=0.616 8+58=0.616,也就是说其分布的均值发生了偏移,也就是说掷到正面的可能性或许更大。具体情况如下图所示(图来自知乎@马同学):

(图注:要是想要值域在[0,1]之间注意归一化,除以一个积分即可)
到这里,我们就大概理解了Beta分布的意义,也可以对前面的解释做一些修正,即:对于一个我们不知道概率是什么,而又有一些合理的猜测时,Beta分布能很好的作为一个表示概率的概率分布。
谈了这么多Beta分布,那这个Beta分布和Dirichlet分布有什么关系呢?
之前我们就提到了,Dirichlet分布也可以用来描述“概率分布的分布”,但是Beta分布描述的是单变量分布,而Dirichlet分布描述的是多变量分布,因此,Beta分布可作为二项分布的先验概率,Dirichlet分布可作为多项分布的先验概率。也就是说,如果说Beta分布是用来解决掷硬币出现正面的概率的,那Dirichlet分布就是用来解决掷骰子得到1点的概率的。
Dirichlet分布的概率密度可以表示为:

可以发现,Dirichlet分布的参数是α,x是变量,代表最可能的概率(也就是期望/均值)。由于x是K维的,所以Dirichlet分布是一个K维的概率函数。
总结来说:
Beta分布是针对二项分布B(n,P)中参数P的分布的估计,而Dirichlet分布是针对多项分布中k各参数的估计。我们可以用Beta分布去计算二项分布中的P,用Dirichlet分布去估计多项分布中的参数。
目标光谱的近似
目前,我们得到了p的近似形式,但是遗憾的是,Dirichlet分布是没有闭式解的,也就是说我们无法得到一个精确的、可由符号表示的解,而是只能通过数值近似来获取近似的数值解。在这里用来获取Dirichlet分布的方法是一种被称作stick breaking的方法。
定义 θ i \theta_i θi为位置, π i \pi_i πi为权重。首先令 θ 1 ∼ G 0 \theta_1 \sim G_0 θ1∼G0, β 1 ∼ B e t a ( 1 , α ) \beta_1 \sim Beta(1,\alpha) β1∼Beta(1,α),那么此时 π 1 = β 1 \pi_1=\beta_1 π1=β1,现在这根stick还剩 1 − p i 1 1-pi_1 1−pi1,我们从里面选出 β 2 \beta_2 β2;接下来,令 θ 2 ∼ G 0 \theta_2 \sim G_0 θ2∼G0, β 2 ∼ B e t a ( 1 , α ) \beta_2 \sim Beta(1,\alpha) β2∼Beta(1,α),此时 π 2 = ( 1 − π 1 ) × β 1 \pi_2=(1-\pi_1)×\beta_1 π2=(1−π1)×β1,现在这根stick还剩 1 − p i 1 − p i 2 1-pi_1-pi_2 1−pi1−pi2,我们从里面选出 β 3 \beta_3 β3;以此类推。用图表示大概为:
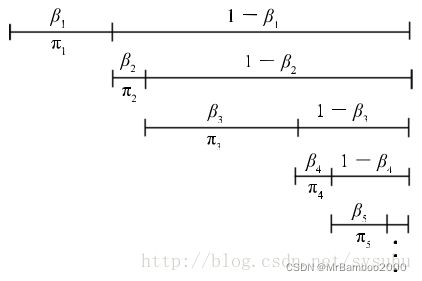
这样我们就得到了 q ( t ∣ t o b s , α ) q(t|t_{obs},\alpha) q(t∣tobs,α)服从的Dirichlet分布G。详细的解析可以看@sysuhu的文章:
从折棍子(Stick Breaking)模型到狄利克雷过程(DP)
一旦分布G被确定,我们就可以根据这个分布采样十组条件概率,并进而得到十组真实目标光谱数据,也就是 T = t 1 , t 2 , . . . , t 10 T={t_1,t_2,...,t_{10}} T=t1,t2,...,t10,然后我们再把这十组光谱数据放到检测器里计算得分:

最后,我们再对这十个得分做一个平均,得到最后的得分:

小结
这篇文章和以往对CEM的改进从思路出发点上就不尽相同。之前那些思路都是想方设法的去抑制图像的背景、突出图像的目标,但是这篇文章将目光直接放在了对给定的目标数据进行改进,而且事实证明取得的效果也很不错。