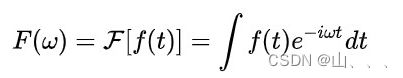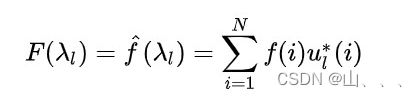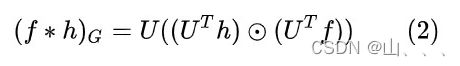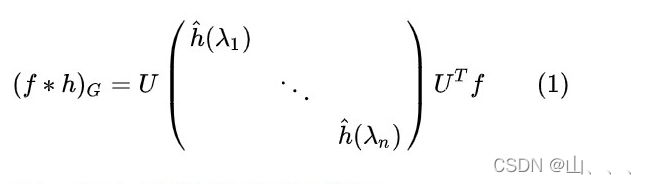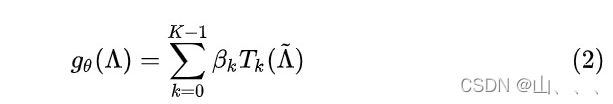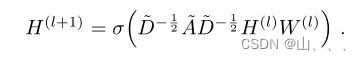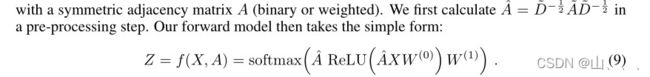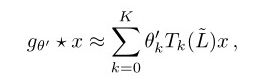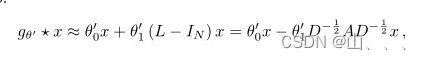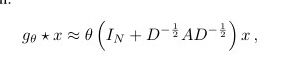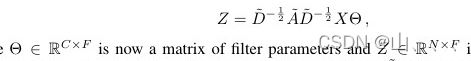基于空间的图卷积网络和基于谱的图卷积网络（spectral-based GCN and spatial-based GCN)

目录

废话：

基于空间的图卷积网络（spatial-based GCN）

基于谱的图卷积网络（spectral-based GCN）

第一部分，从0到1（从传统的傅里叶变换+卷积——>图上的傅里叶变换+卷积）

1. 按照傅里叶变换公式，定义图上的傅里叶变换

2.利用卷积定理得到节点与卷积核的卷积

 3.图卷积网络公式

第二部分，对原始GCN的改进，得到现在常用的模型公式

1.Chebyshev多项式作为GCN卷积核

2.得到常用的GCN模型公式

基于空间和基于谱的图神经网络的对比

---

废话：

很久以前我就看了 《a comprehensive survey on Graph Neural Networks》这篇综述，对于图神经网络的大概分类有了一定的了解，但是并不太清楚具体的细节。

并且自己去了解很多的资料，但是一直没有一个整体的认知。最近看 CS224W: machine learing with graph，又触动了我关于基于空间还是基于谱的认知。然后为了有个清晰的认识，我又看了一遍之前的资料，并且看了《SEMI -SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》（Kipf and Welling 2017）里面关于卷积公式的推导。现在大概有个比较清楚的认识。

基于空间的图卷积网络（spatial-based GCN）

这个部分不过多介绍，参考CS224W: machine learing with graph上提出的这个GCN模型。图神经网络（6）-GNN1_山、、、的博客-CSDN博客图数据的特殊性：1. 没有固定的节点顺序或参考点（排列不变性，不同的节点顺序代表同一个图）2.经常有动态并且多种模式的特征怎么将深度学习应用到graph上呢？？直接将图的邻接矩阵连接节点特征当作输入，应用全连接DNN可以吗？不行！ 这样的话，对于不同size的图用不了，并且这样对节点的顺序敏感！...https://blog.csdn.net/qq_44689178/article/details/123263686?spm=1001.2014.3001.5502

基于谱的图卷积网络（spectral-based GCN）

这个部分的公式推导非常非常麻烦，我搞懂了整个推理过程，没有具体去推导。

公式推导涉及的相关知识点包含：傅里叶变换，矩阵论（拉普拉斯矩阵，谱分解），卷积定理，切比雪夫多项式等。

整个推理过程，我分为两个部分。

第一部分，从0到1（从传统的傅里叶变换+卷积——>图上的傅里叶变换+卷积）

参考下面这位大佬的。我看了很多推导，他说的最清楚明白。

如何理解 Graph Convolutional Network（GCN）？ - 知乎从CNN到GCN的联系与区别——GCN从入门到精（fang）通（qi）1 什么是离散卷积？CNN中卷积发挥什么作用？了…https://www.zhihu.com/question/54504471/answer/332657604说一下理解这篇文章的几个关键点。

1. 按照傅里叶变换公式，定义图上的傅里叶变换

学过积分的都知道，积分就是内积（相乘求和）的极限。

傅里叶变换公式：

图上的傅里叶变换：

 上面的这个f（i） 可以认为就是图神经网络中的H(k)——也就是节点的embeddings

然后把上面这个公式表示为矩阵形式：

2.利用卷积定理得到节点与卷积核的卷积

要得到下面公式：

 这一部分，非常好理解。卷积定理简单解释就是：先卷积再傅里叶变换=先傅里叶变换再卷积

上面这个公式是求的f（节点的embeddings）和h（卷积核）之间的卷积。

那么我们可以先求f（和h（卷积核）之间卷积的傅里叶变换，那么就等于f和h先傅里叶变换再卷积。求得f（和h（卷积核）之间卷积的傅里叶变换，再做一个逆变换就得到f（和h（卷积核）之间的卷积。

由下面这个公式知道，傅里叶变换就是左乘U的转置矩阵，逆变换就是左乘U

 那么，就很容易就得到了

然后，这个公式有其他形式，

 3.图卷积网络公式

通过上面f（节点的embeddings）和h（卷积核）之间的卷积，就得到了第一代GCN。

 之后就是改进。

第二部分，对原始GCN的改进，得到现在常用的模型公式

改进重点就是把卷积核的表示方式做优化，让计算变得简单。

1.Chebyshev多项式作为GCN卷积核

Chebyshev多项式作为GCN卷积核 - 知乎利用Chebyshev多项式拟合卷积核是GCN论文中广泛应用的方法 。在这篇文章中，我会推导相应的公式，并举一个具体的栗子。在之前的回答中（ 如何理解 Graph Convolutional Network（GCN）？），已经推导出了如下GCN的…https://zhuanlan.zhihu.com/p/106687580上面这个连接介绍了具体的细节。最后得到了，Chebyshev多项式作为GCN卷积核的形式。

2.得到常用的GCN模型公式

现在GCN常用的模型公式如下图所示：

图神经网络模型类似于下面这种：

 

 现在讲讲，怎么推导到上面的形式。这部分参考论文《SEMI -SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》。

首先，Chebyshev多项式作为GCN卷积核，那么卷积核与节点embeddings之间的卷积如下图：

 并且

 在论文《SEMI -SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》里面，他提到，（max） 2，并且取K=1阶的Chebyshev多项式。

代入上式很容易得到

化为下面的矩阵形式：

 然后利用一个renormalization trick

 就得到了我们常用的形式： 

 这里面的就是W,而X就是H。

基于空间和基于谱的图神经网络的对比

	基于空间的GNN	基于谱的GNN
效率	可以处理大型图，可以在部分节点中执行，而不是整个图，还可以引入节点采样来提高效率	模型计算成本随着图的大小增加而急剧增加，难以处理大型图。要么计算特征向量，要么处理整个图
灵活性	各种图都行	只可以在无向图上工作，因为有向图上拉普拉斯矩阵没有定义。在有向图上应用，就只能化有向图为无向图。
通用性	在每个节点执行本地卷积，可以在不同的位置和结构之间共享权重	假定一个固定的图，难以添加新的节点

近年来，基于空间的GNN越来越受到关注！！

结束！！