ON LARGE BATCH TRAINING FOR DEEP LEARNING: GENERALIZATION GAP AND SHARP MINIMA
文章目录
-
- 概
- 主要内容
-
- 一些解决办法
Keskar N S, Mudigere D, Nocedal J, et al. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima[J]. arXiv: Learning, 2016.
作者代码
@article{keskar2016on,
title={On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima},
author={Keskar, Nitish Shirish and Mudigere, Dheevatsa and Nocedal, Jorge and Smelyanskiy, Mikhail and Tang, Ping Tak Peter},
journal={arXiv: Learning},
year={2016}}
概
本文主要阐述了一种现象, 就是在我们训练网络的时候, 小的batch_size会比大的batch_size效果更好(表现在准确率上).
主要内容
因为作者主要是进行实验论证的, 所以就介绍一下结果, 我们用LB表示大的batch_size, SB表示小的batch_size.

作者认为, LB会导致参数尖化, 而SB会导致平坦的解, 个人感觉这种就是一个灵敏度的问题. 作者也说, LB会导致 ∇ 2 f ( x ) \nabla^2 f(x) ∇2f(x)呈现某个特征值特别大(绝对值), 其余特征值很小的情况, 而SB的 ∇ 2 f ( x ) \nabla^2 f(x) ∇2f(x)的特征值分布往往比较均匀.
注: 这里的 x x x指的是网络的参数而非样本.
记LB训练后所对应的解为 x l ∗ x^*_l xl∗, 而SB训练后所对应的解为 x s ∗ x^*_s xs∗, 作者沿着俩个点的连续探索其landscape,
f ( a x l ∗ + ( 1 − a ) x s ∗ ) , a ∈ [ − 1 , 2 ] , f(ax^*_l+(1-a)x_s^*), \quad a \in [-1,2], f(axl∗+(1−a)xs∗),a∈[−1,2],
其结果如下
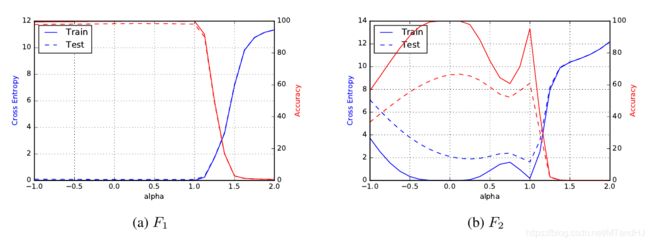

显然, 在 α = 1 \alpha=1 α=1处(即 x = x l ∗ x=x_l^* x=xl∗)左右的未知变化特别大, 这也反应了尖的特性.
一些解决办法
- data augmentation, 效果显著
- conservative training, 即采用proximal下降
x k + 1 = arg min x 1 ∣ B k ∣ ∑ i ∈ B k f i ( x ) + λ 2 ∥ x − x k ∥ 2 2 , (5) \tag{5} x_{k+1} = \argmin_x \frac{1}{|B_k|} \sum_{i \in B_k} f_i(x) + \frac{\lambda}{2} \|x - x_k\|_2^2, xk+1=xargmin∣Bk∣1i∈Bk∑fi(x)+2λ∥x−xk∥22,(5)
其中 f i f_i fi表示输入为第 i i i个样本. - robust training, 即利用原样本和对抗样本进行训练, 但是效果不是很明显(有可能是Goodfellow的机制不对? 新的是不需要利用原样本的).
