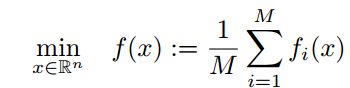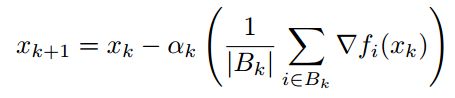Northwestern University & Intel
code: https://github.com/keskarnitish/large-batch-training
* SGD及其变种在batch size增大的时候会有 泛化能力的明显下降 generalization drop/degradation,迄今为止原因还不是很清楚。
* 这篇文章用充足的数值证据支持一个观点:
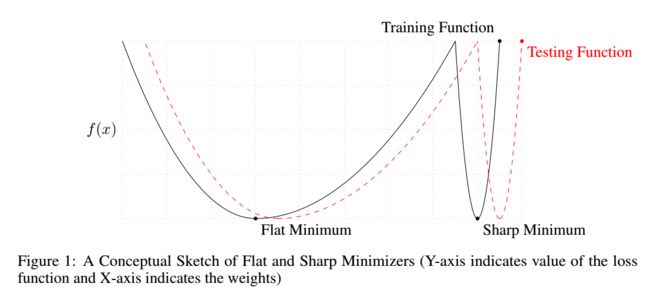
batch size越大,越有可能收敛到比较尖锐的局部极小值。batch size越小,越有可能收敛到比较平稳的局部极小值,实验证明这是因为梯度估计的内在的噪声引起的。
* 讨论了一些经验上的方法帮助large-batch methods消除the generalization gap,总结了一些future research ideas and open questions.
train和test的分布有一定的偏差,局部最小值附近越尖锐,推到test的时候性能下降的越多。
* non-convex optimization(training the network):
f_i:loss function,
x: weights
### SGD and its variants
iteratively taking steps of the form:
* pros:(a)对于强的凸函数能收敛到极小值,对于非凸函数能收敛到驻点(stationary points);(b)能够避免走到鞍点(saddle-point).
* cons:由于方法是序列求解的,batch size一般比较小,在并行上面会有限制。
之前有一些工作在并行SGD上面,但是受小的batch size的限制。
* 一个很自然的并行方案就是增大batch size。 但是会存在generalization gap/drop, 实际中即使对于小的网络,也能有高达5%的精度下降。
* 如果增大batch size,但是不牺牲性能,将有可能增大并行度,很大程度上减少训练时间。
### large-batch(LB) methods的缺点
generalization gap, 尽管训练的时候LB和SB(small-batch)能达到差不多的精度。
可能的原因:
(1) LB相对于SB更加over-fitting
(2) LB方法相对于SB方法缺少explorative(探险,类似强化学习中的概念)的性质,更加倾向于收敛到与初始点接近的局部最小
(3) LB和SB收敛到泛化能力不一样的局部最小
(4) 深度网络需要一定的迭代次数才能使目标函数收敛到泛化能力较好的局部最优,LB方法一般没有SB方法的迭代次数多
(5) LB方法收敛到了saddle points(鞍点)
这篇文章的数据支持了第(2),(3)个推测(这些推测是作者与Yann LeCun的私人交流得到的)
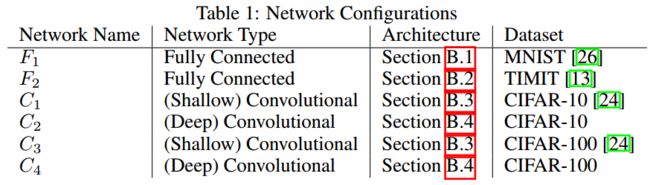
LB: 10% of training data
SB: 256
ADAM optimizer
每个实验5次,不同均匀初始化
在所有实验中,两种方法training acc都很高,但test上面的泛化性能有明显差距。
所有网络训练到loss饱和。
* 作者认为generalization gap不是由于over-fitting(一个表达能力特别强的model在仅有的训练数据上过度训练,从而在某个迭代点达到test acc的峰值,然后又由于这个model在特定的训练集上的学习特性使test acc下降。
这在实验中没有发现,所以early-stopping启发式地防止过拟合不能减小generalization gap)

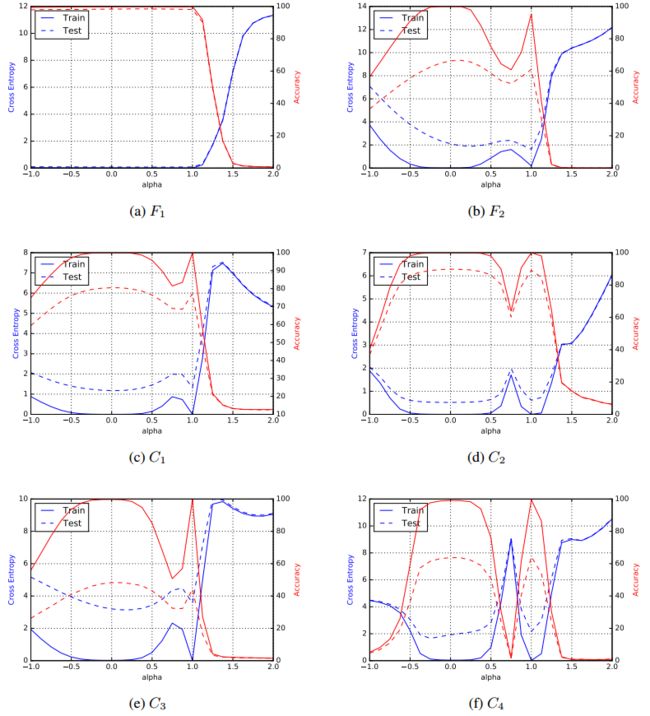
### Parametric plots
描述函数在一维子空间的值的情况,但是并不能提供 在整个空间函数值在 局部最小值附近的情况(sharpness)。
线性
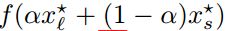 (figure 3)
(figure 3)
曲线
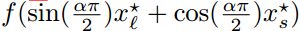 (figure 4)
(figure 4)
### sharpness
找到的解的邻域
A是随机生成的,A^+是A的伪逆
如果A没有确定,就假设是I_nxn
eps = 1e-3, 5e-4
* 用L-BFGS-B解(3)中的max问题,10次迭代。
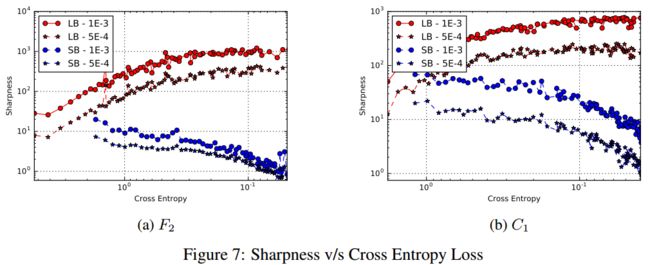
* 两个表中的结果都说明LB的灵敏度更大。SB和LB相差1~2个量级。
### 为什么SB不收敛到sharp minimizers?
因为小的batch size的梯度噪声更大,在尖锐的minimizers的底部,只要有一点噪声,就不是局部最优了,因此会促使其收敛到比较平缓的局部最优(噪声不会使其远离底部)。
batch size越大,test acc会降低,sharpness会增大。
* noise对于远离sharp minimizer并不充分
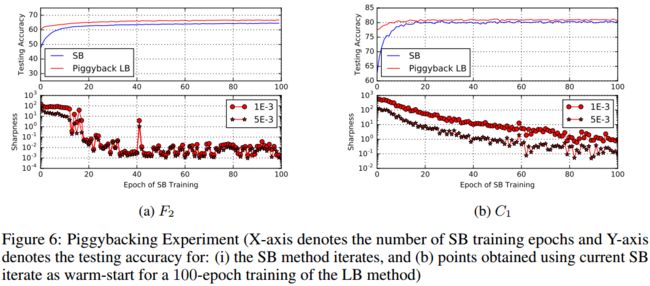
* 首先用0.25% batch size训练100 epochs,每个epochs存下来,以每个epoch作为初始点,用LB的方法训练100 epochs(相当于看不同的初始点对LB的影响,用SB进行预训练)。
然后画acc和sharpness(LB和SB的)
这证明了LB方法确实是会倾向于到达与初始点邻近的sharp minimizers,而SB会远离这种。
当loss减小的时候(往右边去),sharpness差别越大,LB比SB的sharpness更大。
对于SB,sharpness相对恒定,然后才下降。(说明有一个exploitation的阶段,然后在收敛到一个平缓的局部最优)
LB的失败就是因为缺少exploitation的过程,收敛(zooming-in)到与初始点接近的局部最优。但是不知道为什么这种zooming-in是有害的。
### 减轻这种问题的尝试
LB:10%,SB:0.25%
ADAM
* data augmentation
能不能修改loss function的几何结构来使其对LB更友好。
loss function取决于目标函数的形式,训练集的大小和性质。因此用data augmentation的方法。这是domain specific的,但是通常对训练集的操作是可控的。
相当于对网络做了regularization。

对于图像分类,data augmentation:
horizontal reflections, random rotations up to 10 ◦ and random translation of up to 0 : 2 times the size of the image
LB达到了和SB(也做了data augmentation)可比拟的精度, 但是sharpness仍然存在。说明 sensitivity to images contained in neither training nor testing set.
* Conservative Training(保守训练)
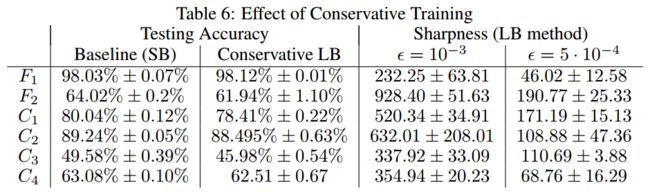
Mu Li et al.[ACM SIGKDD'14] argue that the convergence rate of SGD for the large-batch setting can be improved
by obtaining iterates through the following proximal sub-problem.
motivation: to bettere utilize a batch before moving onto the next one.
用GD,co-ordinate descent or L-BFGS不精确的迭代3-5次求解,他们证明这不仅提高了SGD的收敛速度,而且改善了凸机器学习问题的经验性能。
更充分利用一个batch的基本思想不只是针对凸的问题,对于DL也一样,但是没有理论保证。
本文用ADAM进行3次迭代解上述问题。\lambda=1e-3,
这种方法也能够提升test acc,但是灵敏度的问题还是没有解决。
* Robust training
求解最坏情况下的cost。
直接使用这种技巧是不可行的,因为包含一个大规模的SOCP(二阶锥规划)问题,计算代价太高了
在DL中,鲁棒性有两个相互依赖的概念:对数据鲁棒和对解鲁棒。
前者说明f本质上是一个统计模型,后者将f看做是黑箱。
[36]中说对 (相对于数据) 解的鲁棒性和adversarial training[15]是等价的.
由于data augmentation一定程度上是成功的,很自然想到adversarial training是否有效。
[15]中说,adversarial training也是想要人为地增广训练集,但是不像随机增广,是用的模型的灵敏度来构造新的样本。
尽管这很直观,但是在实验中没有发现这能够改善泛化能力下降的问题。
同时,实验也发现,用[44]中stability training的方法也没能提升泛化能力。
adversarial training,或者其他任何形时的robust training能不能用来提升large-batch training的性能,仍然待验证。
### 总结与讨论
* 通过数值实验证明了large-batch training确实存在更容易收敛到尖锐的局部最优的情况,从而使其泛化能力下降。文章中用了data augmentation或者保守训练的尝试来减轻这个问题,能够在一定程度上缓解泛化能力的下降,但是不能解决收敛到尖锐的局部最优的问题。
* 可能有希望的方法包括dynamic sampling或者switching-based strategy,在初始的一些epochs利用small batches,然后逐渐或者突然转变为large-batch方法。
例如[7]中的方法。
用SB方法初始化,然后结合其他方法,是future research的方向。
* 之前很多工作说明了DL中,loss surface上存在很多局部最优,大部分深度相似。本文说明在相似深度上的局部最优的sharpness会不一样。
the relative sharpness and frequency of minimizers on the loss surface remains to be explored theoretically.
* open questions:
(a) 能否证明large-batch方法收敛到sharp minimizers?
(b) 两种不同的局部最小点的相对密度如何?
(c) 能否设计网络时考虑解决LB方法的灵敏度的问题?
(d) 网络能否被某种方法初始化,使得LB方法能成功?
(e) 能否用算法或者可调控的方法引导LB方法远离sharp minimizers?
LB方法如果能够解决,很明显的一个意义就是能够使得在多核CPU、甚至多节点的CPU机器上能够很大程度地实现DL的并行加速。
From WizNote