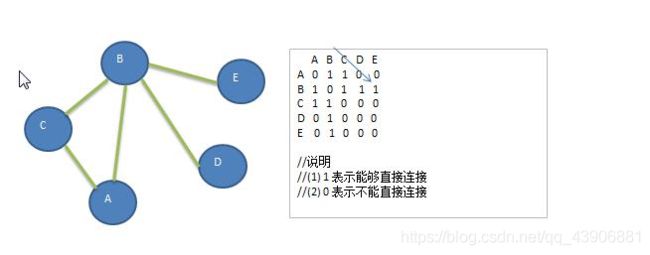
无向图的广度优先遍历算法(bfs)
基本介绍
- 图的广度优先搜索(Broad First Search) 。
- 类似于一个 分层搜索的过程,广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来
访问这些结点的邻接结点
算法步骤
- 访问初始结点 v 并标记结点 v 为已访问。
- 结点 v 入队列
- 当队列非空时,继续执行,否则算法结束。
- 出队列,取得队头结点 u。
- 查找结点 u 的第一个邻接结点 w。
- 若结点 u 的邻接结点 w 不存在,则转到步骤 3;否则循环执行以下三个步骤:
6.1 若结点 w 尚未被访问,则访问结点 w 并标记为已访问。
6.2 结点 w 入队列
6.3 查找结点 u 的继 w 邻接结点后的下一个邻接结点 w,转到步骤 6。
注:图的创建及方法调用等在下面
代码实现1(核心方法)
注意看代码中的注释
注:
- 所有节点都已经存放到了全局变量 private ArrayList vertexList中,{“A”,“B”,“C”,“D”,“E”}
- 邻接矩阵是用来找邻接节点的
- isVisited[]用于标记当前节点是否被访问过
- vertexList则是用来打印元素的(vertexList里的下标是和邻接矩阵的行列下标一一对应的)
//对一个结点进行广度优先遍历的算法
private void bfs(boolean[] isVisited,int i){
int u; // 表示队列的头结点对应的下标
int w; // 邻接节点的下标
//队列, 记录节点访问的顺序
Queue<Integer> queue = new LinkedList();
//访问节点,输出节点信息
System.out.print(vertexList.get(i)+"=>");
//标记为已访问
isVisited[i] = true;
//将节点加入队列
queue.offer(i);
while (! queue.isEmpty()){
//取出队列的头结点的下标(第一次就是A节点)
u = queue.poll();
//得到第一个邻接节点的下标w
w = getFirstNeighbor(u);
//注: 该内层while循环里不会有出队操作,因为当目标节点所在层遍历完了之后,还要从它的邻接节点里挑选下层外循环的目标节点(B),来继续找其它层的元素!!!(出队了就找不到了)
//注: 在这个while循环里,我们将完成对(以A节点为例)目标节点的所有邻接节点的(即属于一个层的)访问
while (w != -1){ //找到
//如果没被访问过
if (!isVisited[w]){
System.out.print(vertexList.get(w)+"=>");
//标记为已访问
isVisited[w] = true;
//入队
queue.offer(w);
}else {
//寻找u节点除了w节点以外的别的邻接节点
// (若u以 A 的下标0为例, 则第一轮循环执行这条语句时的w就是 1(B),执行之后就是 2(C))
w = getNextNeighbor(u,w);
}
}
}
}
运行结果
广度优先遍历:
A=>B=>C=>D=>E=>
代码实现2(bfs时要用的封装的方法)
- getFirstNeighbor(int index)—得到目标节点的第一个邻接节点的下标,遍历邻接矩阵的index行,如果有元素大于0就直接返回下标!
- getNextNeighbor(int v1, int v2)—根据前一个邻接节点的下标来获取下一个邻接节点的下标!
//得到目标节点的第一个邻接节点的下标
/**
* @param index
* @return 如果存在就返回对应的下标, 否则返回-1
*/
public int getFirstNeighbor(int index){
for (int j = 0; j < vertexList.size(); j++) {
if (edges[index][j] > 0){
return j;
}
}
return -1;
}
//根据前一个邻接节点的下标来获取下一个邻接节点
/**
*
* @param v1 指的是一个节点的下标
* @param v2 指的是该节点的邻接节点
* @return 我们要找的是 v1节点的邻接节点v2的下一个邻接节点的下标j!
*/
public int getNextNeighbor(int v1, int v2){
for (int j = v2 + 1; j < vertexList.size(); j++) {
if (edges[v1][j] > 0){
return j;
}
}
return -1;
}
代码实现3(图的创建)
public class Graph {
private ArrayList<String> vertexList;//存储定点集合
private int[][] edges; //存储图对应的邻接矩阵
//定义一个数组boolean[] , 记录某个节点是否被访问
private boolean[] isVisited;
public static void main(String[] args) {
//节点的个数
int n = 8;
String VertexValue[] = {"A","B","C","D","E"};
//创建图对象
Graph graph = new Graph(n);
//循环的添加节点到vertex中
for (String vertex : VertexValue) {
graph.insertVertex(vertex);
}
//更新边的关系 //A-B A-C B-C B-D B-E
graph.insertEdge(0,1,1); //A-B
graph.insertEdge(0,2,1); //A-C
graph.insertEdge(1,2,1); //B-C
graph.insertEdge(1,3,1); //B-D
graph.insertEdge(1,4,1); //B-E
//显示矩阵
graph.showGraph();
//测试bfs()
System.out.println("广度优先遍历:");
graph.isVisited = new boolean[graph.vertexList.size()];
graph.bfs(graph.isVisited,0);
}
//构造器
public Graph(int n){
//初始化矩阵 和 vertexList
edges = new int[n][n];
vertexList = new ArrayList<>();
}
//图中常用的方法
//显示图对应的邻接矩阵
public void showGraph(){
for (int[] link :
edges) {
System.out.println(Arrays.toString(link));
}
}
//插入节点
public void insertVertex(String vertex){
vertexList.add(vertex);
}
//添加边,构造邻接矩阵
/**
*
* @param v1 表示点的下标即是 第几个顶点 “A”-"B" "A"->0 "B"->1
* @param v2 第二个顶点对应的下标
* @param weight 表示权值
*/
public void insertEdge(int v1, int v2, int weight){
edges[v1][v2] = weight;
edges[v2][v1] = weight;
}
运行结果
[0, 1, 1, 0, 0, 0, 0, 0]
[1, 0, 1, 1, 1, 0, 0, 0]
[1, 1, 0, 0, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0]
广度优先遍历:
A=>B=>C=>D=>E=>