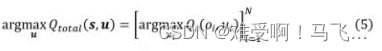多智能体强化学习之值函数分解：VDN、QMIX、QTRAN系列优缺点分析（转载）

这个博客是转载网易伏羲实验室的博客，为了让自己能更详细的记住这个博客的内容，所以决定手动抄写一遍。

考虑到一些道友的爱好，我会用一些比较诙谐的语言来形象的解释一些枯燥的学术定理。

写在前面的个人总结一下：

所谓的值函数分解，其实就是寻找到一个合理的方法来合理的，精确的表示每个独立agent的动作值$Q_i$与中心网络中的$Q_{tot}$之间的关系。因为多智能体强化学习模型训练参数是依赖$Q_{tot}$的，多智能体强化学习通过中心化网络接收全局状态信息s并训练每个agent的参数，其主要目的是解决单个智能体不具全局观察能力的缺点。每一轮训练结束后，单个agent独立执行自己的动作。但是，如果不能准确表示$Q_i$与$Q_{tot}$之间的关系，那么训练出来的模型效果会很差。
值分解的目的是在中心化网络中分解$Q_{tot}$。

Multi-agent RL（MARL）是最近强化学习领域的研究热点，至于为什么热，我认为有两点原因，第一，确实可以解决一些问题，第二，这是最近水论文的一个方向。
最近，MARL的主要研究方向分为两点：communication和centralized traning decentralized execution（CTDE）。简单的来说，communication就是研究RL agent之间的通信问题，这个领域很有意思，网易伏羲实验室的一个做通信的大佬从通信领域特有的思想写了一个paper。CTDE其实就是值分解，简单来讲就是讲中心化训练然后分散执行，即在训练阶段讲所有agent的Q以加性的方式组合到一块，在中心层训练，训练好后每个agent各做各的，这样做有两个缺点：1）出现“lazy agent”，比如DOTA或者LOL游戏中，一个最强王者带四个青铜打比赛。那个王者三路杀通关，连野区都不放过。四个青铜什么事都不做，就在那挂机，甚至送人头都能赢。2）中心化训练会严重拖慢训练速度，因为每次训练都要等所有agent都上传数据才行。然而事实上是，我们五排的时候，有个卡B用2G网玩，加载百分数增加的比滴水还蛮。这个我们可以参考VDN这个paper。

言归正传

MARL中的难点

• 部分可观测性，这个很简单，对于LOL或者dota来讲，每个玩家都无法观察到全局地图。在论文中，我们习惯记agent的观察为o，全局状态为s。
• 不稳定性。不稳定性主要还是由部分可观测性引起的。简单来讲就是agent执行动作是根据自己的观察o来做决定的，而不是全局状态s，因此每个agent的动作都可能导致另一个agent的在这一时刻执行动作的reward=1，下一时刻可能就reward=-1。形象的来讲，你在玩LOL是，我方打野前来上路抓人，这时你习惯性的上去卖一波血，演一下。但是，当你演到一半时，我方打野发现对面中单和打野同时消失在视野中，因此选择去继续打野。但是，他没通知你。因为你没开语音，又因为他是祖安人，发言数量被限制。这时，你还是选择继续卖，当你发现在不来时已经晚了，此时对方中野已经断了你的后路…然后下面难免一波来自祖安的问候。例如一些全家升天…我给你妈妈打电话，结果，尼玛挂了。。。.等一些我们都听不等的。
  总结一下造成不稳定性的原因：
• 部分可观测性导致o对应的全局状态s有很多。
• 所有agent都在不断更新策略，因此agent选择的都做也在不断变化。

关于值分解

我们先使用LOL（没玩过lol的可以考虑dota或者农药等游戏）有些解释一下，为什么要进行值分解，然后再用枯燥的学术语言介绍一下，这样大家就懂了。
正常来讲，我们平时单排或者单独匹配的时候，都是乱打，青铜组甚至不看小地图，也不发警示信号，更不可能插眼了，再说了，插眼也没用，因为也不看小地图。这时，五个玩家就是完全处于部分可观测性状态，这是他们眼里只有自己的显示器。这时，他们只会根据自己的现状执行动作，只有活下来的人才配补刀。
玩久了之后，有些人慢慢学会了一些技术，比如时不时的看小地图，看看其他几路的队友，这就是CTDE，即使用CTDE来让自己能观察到全局信息。再LOL中，CTDE就是插眼，看小地图，发送各种警示信号。
对于职业战队来讲，他们还有一个更牛逼的设置，就是教练，教练观察全局信息，指导每一步的任务。再MARL中，指导教练就是CTDE中的centralized 。这下的懂了吧。CTDE就是主教练根据五个选手的全局状态做出决策，是开团，还是传中，还是放弃上路，围攻大龙，等等。

从学术角度来讲，CTDE就是去训练一个全局的$Q_{total}(s,u)$，它考虑全局信息，可以直观的克服MARL的不稳定性。但是需要注意，即使训练出$Q_{total}(s,u)$也不表示就可以解决问题了，因为每个agent还是无法得到全局状态信息s，也就是说，这个时候，一个野队有了教练，却不知道怎么用这个教练，因为他们的蓝牙耳机并没有连上。针对这一问题，诸多大神相继提出了VDN、QMIX、QTRAN，下面我们将诸葛介绍这三个算法，并分析他们的优缺点。

VDN

前面说了，一个野队有了教练，但是没有蓝牙耳机，因此主教练无法指挥队员，队员也无法从主教练口中了解全局状态s。针对这一问题，VDN提出了使用$Q_i(o_i,u_i)$对$Q_{total}(s,u)$进行加性分解。其中，$Q_i(o_i,u_i)$表示每个agent的动作值。为什么叫加性分解呢，看下面这个公式：
$Q_{total}(s,u)={\sum }_i^N(Q_i(o_i,u_i))$,N表示智能体的个数。
在得到这个总的$Q_{total}(s,u)$之后，VDN就是简单的使用DQN的更新方式来训练参数了。就这么简单。

这个时候，梯度反向传播算法会在更新梯度差的过程中，讲全局所有的状态信息s传播给每个agent。这个想法是不是很有点意思。
但是，QMIX说，不行，VDN的方法不行。他有很多缺点，，，于是

QMIX

1. 进一步理解值分解

在介绍QMIX之前，我们还需要重新梳理一下值分解。
网易伏羲实验室的大佬认为啊，VDN提出的$Q_{total}(s,u)={\sum }_i^N(Q_i(o_i,u_i))$严格来讲不叫值分解，而是叫值近似，他就是用所有agent的动作值Q的和的形式来近似$Q_{total}(s,u)$，这是不对的。确实，因为VDN的作者也在他的paper很隐晦的承认了，翻译他的原话就是：$Q_{total}(s,u)$是我们假设系统的联合动作-价值函数可以被加性分解为跨agent的价值函数。原话是这么说的：“The main assumption we make and exploit is that the joint action-value function for the system can be additively decomposed into value functions across agents,”
怎么样，是不是很有意思？

我在慕尼黑工业大学的导师是专搞数学的，他跟我说，sun，你在看论文的时候，如果想快速改进算法，你就看他们的假设。我在你们计算机科学领域的一些文章中看了很多不合理的假设。如果你想改进这个文章，你就从假设入手。因为不合理的假设会让这个算法受到很多局限，你就去解决这些问题。

上面这句话送给很多还在博士期间为了论文而苦苦挣扎的民工们。以后，你们据从这入手，保证你快准狠，然后找个你们学校数学系的大佬做靠山，挂他二作，这事就成了。
回到主题，事实上，这个$Q_{total}(s,u)$的真实值我们是不知道的，这个时候的VDN就是一言堂加想当然。此外，退一万步讲，就算我们知道了$Q_{total}(s,u)$的真实值又能怎么样呢？因为我们还受到部分可观测性的限制。所以，QMIX调整了$Q_{total}(s,u)$的计算方式，来进一步的近似$Q_{total}(s,u)$。
。

2. VDN的缺点

VDN的假设，就是他的缺点。他们想当然的认为$Q_i(o_i,u_i)$和$Q_{total}(s,u)$之间的关系就是加性关系，就是1+1=2的关系。然而事实上，就我对机器学习的了解，它不可能这么简单。绝对是非常复杂的非线性关系。
退一万步来讲，即使$Q_i(o_i,u_i)$和$Q_{total}(s,u)$之间存在简单的加性关系，那么这也只是一少部分的任务。因此VDN的一般性较差。她不能处理更复杂的关系了。于是乎，QMIX的作者就想了，既然已经铁着头要讲end to end learning进行到底了，那为什么不更彻底一点呢，我们直接通过神经网络来训练$Q_i(o_i,u_i)$和$Q_{total}(s,u)$之间的关系，这不是更靠谱吗？是吧，我也是这么认为的，毕竟刚入门机器学习或者深度学习的学生都听过或看过这句话：“神经网络具有很强的非线性拟合能力，它能以任何方式来逼近任何复杂的非线性函数。”但是拟合的越完美，往往越容易出现过拟合。
所以，请看QMIX的思想，讲训练进行到底…

3. QMIX的思想

由于VDN不能表示复杂的$Q_{total}(s,u)$，因此QMIX选择使用一个神经网络$f$来近似$Q_{total}(s,u)$。因为神经网络具有强大的表示能力。往往，只说说这句话的人就是再坑新手，为什么，这句话有个前提就是：在数据量和神经网络参数量允许的情况下，神经网络才具有强大的表示能力。
这其实也是在给QMIX挖坑。我还是那句话，挖坑害别人者，终将掉进自己的坑。
回到主线，于是乎，QMIX想再实现集中式训练的同时还能使用任何可用的状态信息。也就是说，QMIX在近似$Q_{total}(s,u)$时使用了全局状态信息s。换汤不换药啊，具体的参数更新方式还是DQN的那一套。不变，
在训练时，是有问题的。神经网络$f$虽然很牛，可以用任何姿势去欺负任何可怜的，妖娆的函数，但是并不表示$f$可以随便学。也就是说，如果$f$学的好了，学到一个很精确的$Q_{total}(s,u)$，那便是晴天。但是，如果学到的$Q_{total}(s,u)$很差，那还怎么更新参数？这时候再加上自举引起的值高估，那系统肯定崩了。
因此，QMIX限制$f$中的所有参数全部非负，从而满足下面这个条件：
$\frac{\partial Q_{total}}{\partial Q_i}\ge 0,\forall i$
这个约束可以让$Q_{total}(s,u)$和$Q_i(o,u)$之间满足单调性。
从而确保
$arg{\max }_u{Q}_{total}(s,u)=[arg{\max }_1{Q}_1(o_1,u_1),...,arg{\max }_N{Q}_N(o_N,u_N)]$
看明白什么意思了吗？意思就是说，这个时候，从$Q_{total}(s,u)$中和从$[arg{\max }_1{Q}_1(o_1,u_1),...,arg{\max }_N{Q}_N(o_N,u_N)]$选出的最优动作是一样的了。

网易大佬给出的解释是：
我放权给$f$，让它自己去训练，去近似。但是他们能乱近似，他得守住$\frac{\partial Q_{total}}{\partial Q_i}\ge 0,\forall i$这个底线。
但是，不出意外，意外就来了。因为假设和约束都是很要命的，特别是对于环境复杂，网络结构又很难搞的DRL了。
你敢有约束，我就敢一般性很差给你看。

4. hypernetwork方法

QMIX使用hypernetwork方法专门训练了一个神经网络$g(s)$,输入s后得到$f$的参数$w,b$。然后将$Q_i(o_i,u_i)$输入$f$得到$Q_{total}(s,u)$。具体方法也不难，自己去看文章中的图吧。

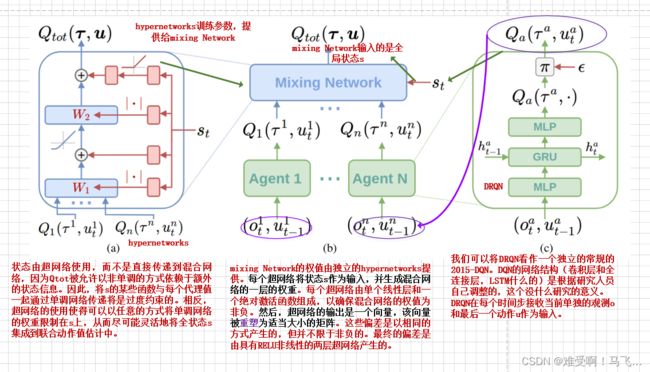
总结一下，VDN假设$Q_{total}(s,u)$和$Q_i(o,u)$之间满足加性关系，QMIX假设$Q_{total}(s,u)$和$Q_i(o,u)$之间满足单调性。相对来讲，QMIX有所进步，但是也不一定就是单调关系。因此这两种方法只能解决部分问题。

于是乎，QTRAN又出来作妖了。为什么说他作妖呢！看下面。

QTRAN

1. QTRAN的提出

首先啊，QTRAN的作者就很不讲武德的使用了我导师的那套水论文，哦不，发论文的套路，上来就殴打VDN和QMIX这两个50岁的老年人。并扬言要释放$Q_{total}(s,u)$和$Q_i(o,u)$之间累加性和单调性的束缚。也就是去分解可以分解的任务。
但是其主要宗旨还是保证个体最有动作$\bar{u}$和联合最优动作$u^{\ast }$是相同的。也就是

QTRAN认为只要满足上面这个公式，那么就称$Q_{total}(s,u)$和$Q_i(o,u)$满足IGM（individual-Global-max）.他们认为只要$Q_{total}(s,u)$和$Q_i(o,u)$满足IGM，那么$Q_{total}(s,u)$和$Q_i(o,u)$的具体关系我们就不需要考虑了。
接下来QTRAN是怎么做的呢？

2. QTRAN的做法

第一：直接学习一个全局的$Q_{total}(s,u)$，

意思就是直接去学习一个真实的$Q_{total}^{\ast }(s,u)$.
注意，VDN的做法是QMIX近似$Q_{total}(s,u)$，QTRAN的做法是学习一个$Q_{total}(s,u)$。
那么问题来了，前面说了，部分可观测性的存在导致我们无法使用$Q_{total}(s,u)$进行决策，但是我们可以使用$Q_{total}(s,u)$来更新$Q_i(o,u)$。只要我们建立$Q_{total}(s,u)$和$Q_i(o,u)$之间的关系，就可以成功的使用真实的$Q_{total}^{\ast }(s,u)$来更新$Q_i(o,u)$。那么，决策的时候使用$Q_i(o,u)$就可以了。接下来的问题就成了如何建立$Q_{total}(s,u)$和$Q_i(o,u)$之间的关系。

第二，建立$Q_{total}(s,u)$和$Q_i(o,u)$之间的关系

QTRAN先通过累加$Q_i(o,u)$来近似$Q_{total}(s,u)$，得到$Q_{total}^{’}(s,u)$笑死！。第一步就直接打自己的脸，掉自己的坑，如果近似失败，两者差很多怎么办？
他们的办法是引入一个$V(s)$来弥补$Q_{total}(s,u)$和$Q_{total}^{’}(s,u)$之间的误差。但是，$V(s)$如何得到，我们又该如何使用$Q_{total}(s,u)$来更新$Q_i(o,u)$呢
这就要牵扯到IGM了

下面我直接截图吧，累了

总结

讲到最后，值分解的目的就是通过一个合理的，准确的方式将全局状态信息引入到每个agent的更新梯度中。你所提出的方法越精妙，约束越少，就越好。